Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Теорема 11. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну

⇐ ПредыдущаяСтр 5 из 9Следующая ⇒
Рис. 18

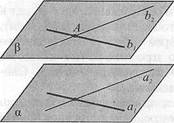
Доказательство. Пусть а — плоскость, А — не лежащая на ней точ­ка. Чтобы через данную точку А про­вести плоскость р, параллельную плос­кости а, сначала в плоскости а прове­дем какие-нибудь две пересекающиеся прямые ах и а2 (рис.18). Потом через данную точку А проведем параллельные им прямые Ьх и Ь2. Прямые Ъг и Ь2 определяют единственную плоскость Р (теорема 2). А по следствию теоремы 8 Р1|а. Единственность такой плоскости р не вызывает сомнений.

Следствие. Две плоскости, параллельные третьей плоскости, параллельны.

Следствие легко доказывается с помощью теоремы 11. Если даны три плоскости а, р, у, такие, что а || у, р* || у, то ясно, что р || а. Действительно, если предположим, что а п Р = Ъ (прямая), то через некоторую точку А прямой Ъ проходили бы две плоскости, парал­лельные плоскости у. А это противоречит теореме 11. Поэтому а || р.

Вопросы и задания

1. Какие плоскости называются параллельными?

2. Докажите теорему о признаке параллельности двух плоскостей.

3. Докажите, что если две параллельные плоскости пересекаются третьей, то
прямые пересечения параллельны.

•4. Докажите, что отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

■ ■ • 18


 

5. Докажите, что через точку вне данной плоскости можно провести плоскость,
параллельную данной, и притом только одну.

6. Повторите и запомните следствия теорем.

7. В окружающей вас обстановке найдите примеры параллельных плоскостей,
плоскости и параллельной ей прямой.

Задачи

49. Две прямые плоскости а параллельны плоскости р. Следует ли
отсюда, что а || р?

Рис. 19
 

50. а \\ р. Докажите, что каждая прямая плоскости а параллельна
плоскости р.

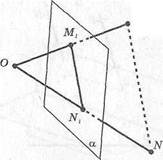
51. Отрезки О А, ОВ и ОС не лежат в одной плоскости, Докажите,
что плоскость, проходящая через их середины, параллельна плос­
кости АВС.

52. Могут ли быть равными отрез­
ки не параллельных прямых,
заключенные между двумя
параллельными прямыми?

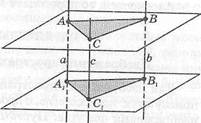
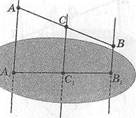
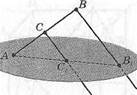
53. Через вершины треугольни­
ка АВС, лежащего в одной из
двух параллельных плоскос­
тей, проведены параллельные
прямые, пересекающие вторую
плоскость в точках А1,В1,С1.
 Докажите равенство треуголь­
ников АВС и А1В1С1 (рис.19).

В

54. Две параллельные плоскости а и р пересекают сторону АВ тре­
угольника АВС в точках В и Ох, а сторону ВС соответственно в
точках Е и Ег Найдите длину отрезка ВЕ, если \ВЩ = 12 см,
15^1 = 18 см, ЩЕ^ = 54 см.

55. Плоскость у пересекает плоскости а и р по параллельным пря­
мым. Следует ли из этого, что плоскости аир параллельны?

56. Плоскости аир пересекаются. Докажите, что любая плоскость
пространства пересекает хотя бы одну из плоскостей а, р.

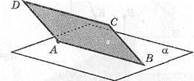
57. Через вершины параллелограмма АВСВ, лежащего в одной из
двух параллельных плоскостей, проведены параллельные прямые,
пересекающие вторую плоскость в точках А^В^С^^. Докажите,
что четырехугольник А1,ВХ,С1,В1 тоже параллелограмм.



58. Прямая а параллельна плоскости а.
Как через прямую а провести плос­
кость, параллельную а?

/А/     /
У г* / 1   ^ \ \ \> /
    \  
    7, у
Рис. 20

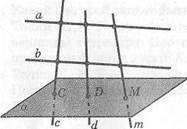
59. Три прямые, проходящие через
одну точку, пересекают данную
плоскость в точках А, В, С, а парал­
лельную ей плоскость в точках А1, Щ,
Сг Докажите подобие треугольников
АВС и А^В^ (рис. 20).

60. АВСОЕРА — не плоская
замкнутая ломаная из шести звеньев.
Докажите, что если [АВ] \\ [ОЕ], [ВС\ \\

[ЕР] и [СО] || [РА], то \АВ\ = \ОЕ\, \ВС\ = \ЕР\ и \СО\ = \РА\. 61. Докажите, что если прямая пересекает одну из двух параллельных плоскостей, то пересекает и другую.

§9. ПАРАЛЛЕЛЬНОЕ ПРОЕКТИРОВАНИЕ Изображение пространственных фигур на плоскости

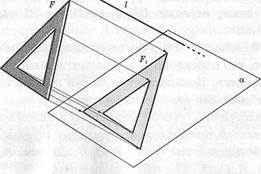
Для изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием. Объясним этот способ изображения фигуры. Пусть даны плоскость а и пространственная фигура Р (рис. 21). Берем произвольную прямую I, пересекающую плоскость а. Проведем через каждую точку фигуры Р прямую, параллельную /. Точки пересечения всех этих прямых с плоскостью а образуют плоскую фигуру Рг

Полученную таким образом фигуру Рх называют параллельной проекцией (изображением) фигуры Р на плоскость при проектировании параллельно /. При этом прямую / называют проектирующей прямой,

плоскость а— плоскостью проекций {плоскостью чертежа).

Рис. 21

Такой способ изобра­жения пространственной фигуры на плоскости со­ответствует зрительному восприятию фигуры при рассматривании ее издали. Отметим некоторые свойства изображения фигуры на плоскости, вы­текающие из описанного ее построения.



I)

в^Й

Рис. 22

 

Рис. 23

Теорема 12 (о проекциях отрезков). Если проектируемые отрезки не параллельны проектирующей прямой, то:

1) проекцией отрезка является отрезок;

2) параллельные отрезки проектируются в параллельные отрезки
или отрезки одной прямой;

3) длины проекций параллельных отрезков или отрезков одной
прямой относятся как длины проектируемых отрезков.

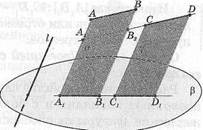
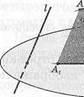
] Доказательство. 1) Все прямые, параллельные проекти­рующей прямой I и пересекающие данный отрезок АВ, заполняют полосу а —часть плоскости, ограниченную параллельными прямы­ми ААг и ВВГ Полоса а пересекает плоскость проекций р по отрез­ку АгВг Этот отрезок—проекция отрезка АВ на плоскость р (рис.22).

2) Пусть проектируемые отрезки АВ и СО параллельны. Все
пересекающие их прямые, параллельные I, заполняют полосы а и
у — части одной плоскости (рис. 28) или параллельных плоскостей.
Полосы а и у пересекают плоскость |3 соответственно по отрезкам
одной прямой или по параллельным отрезкам А1В1 и С1В1 — проек­
циям данных отрезков на плоскость р.

3) а) Если проектируемые отрезки АВ и СО расположены на
одной прямой (рис.22), то \АгВ^: 10^1 = \АВ\: \СО\ (по теореме Фалеса).

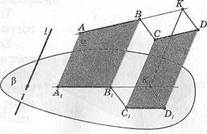
б) Если отрезки АВ и СО параллельны, а их проекции А1В1 и С11Э1 лежат на одной прямой (рис. 23), то АВВ2А2 — параллелограмм. В этом случае: [АД1: |С11)1| = \А2В2\: \СО\ =

в) Если проекции А1В1 и С1О1 данных параллельных отрезков АВ и СО не лежат на одной пря­мой (рис. 24), то построим парал­лелограмм СОКВ. Его проекция— параллелограмм С11)1Ж1В1. Значит, 1ДД1: 1ОД1 = [АД |: [ВД =

Рис.24

= \АВ\: \ВЩ = |АВ|: \СЦ.


 




Итак, всегда 1^.8^:!С1^01| = \АВ\: \СВ\, т.е. длины проекций парал­лельных отрезков или отрезков одной прямой относятся как длины проектируемых отрезков.

Следствие. Проекцией середины отрезка является середина его проекции.

Рассмотренные свойства параллельного проектирования отрезков позволяют наглядно и с большей определенностью изображать неплоские фигуры на плоскости.

Изображением фигуры называют любую плоскую фигуру, подоб­ную проекции данной фигуры на некоторую плоскость.

Из теоремы о проекциях отрезков следует, что треугольник, в том числе равносторонний, равнобедренный и прямоугольный, можно изображать произвольным треугольником. Параллелограмм, в том числе ромб, прямоугольник, квадрат, можно изображать произволь­ным параллелограммом.

Способы задания плоскости и параллельного проектирования часто используют при построении сечений многогранников. Определение многогранника мы дадим в 11 классе. Пока ограничимся двумя простейшими примерами многогранников: прямоугольным паралле­лепипедом и тетраэдром.

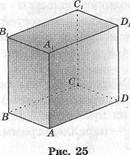
ПрямоуголъныйпараллелепипедшАееп 6 гра­ней, 12 ребер, 8 вершин (рис. 25). Все его гра­ни — прямоугольники. Один из видов прямо­угольного параллелепипеда — куб. Все грани куба—равные квадраты. Когда говорят "парал­лелепипед АВСВ А^В^С^)", имеют в виду, что его основание АВСВ, а боковые ребра ААХ, ВВг, СС1,ВВ1.

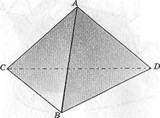
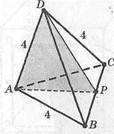
Тетраэдр (треугольная пирамида) имеет 4 грани, 6 ребер, 4 вершины (рис.26). Каждая грань тетраэдра — треугольник. Если все ребра тетраэдра равны, его называют правильным тетраэдром.


Таким образом, что такое сечение мно­гогранника?

Рис. 26

Если, по крайней мере, две точки мно­гогранника лежат по разные стороны от плоскости, то говорят, что плоскость пересе­кает многогранник. В этом случае ее назы­вают секущей плоскостью. Фигура, состоя­щая из всех точек, общих для многогранника и секущей плоскости, называется сечением многогранника данной плоскостью.


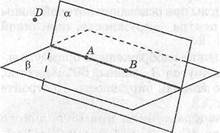
На рисунке 27 изображены тетраэдр АВСВ -А

и секущая плоскость р. Точки А и В лежат по
разные стороны от секущей плоскости. \ ■

Четырехугольник ЬМЫК — сечение данного тетраэдра плоскостью (3.

Чтобы построить сечение многогранника ■ ■'

плоскостью, надо задать эту плоскость: указать ° ч
три (не лежащие на одной прямой) точки, через ". '

которые проходит эта плоскость, или точку и

Прямую И Т.Д.. V В

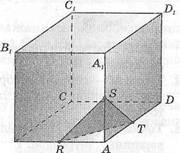
Пример, Постройте сечение куба Рис. 27

АВСВА1В1С^В1 плоскостью, проходящей через точки Е,8,Т — середины ребер АВ, ААХ, АВ (рис. 28, а).

Решение. Точки Е, 8, Т не лежат на одной прямой, поэтому задают некоторую плоскость. Требуется на данном изображении куба построить изображение указанного сечения. Точки Е и 8 лежат в плоскости грани АВВ1А1 куба и в секущей плоскости. Значит, эти плоскости пересекаются по прямой А9. Секущая плоскость пересекает квадрат АВВ^ по отрезку А5. Аналогично убеждаемся, что две другие грани куба секущая плоскость пересекает по отрезкам 8Т, ВТ. Построив их, получим треугольник Е8Т. Это и есть искомое сечение (рис. 28, б).

А

Т

■:*>

.. аА. \С
в
в
В

б)

а)

Рис. 28

 

Вопросы и задания

1. 2. 3. 4. 5**.

Как подучить параллельную проекцию: а) точки; б) фигуры?

Какая фигура является параллельной проекцией: а) отрезка; б) прямой?

Какие свойства фигур сохраняются при параллельном проектировании?

А какие не сохраняются?

Приведите реальные примеры проектирования.

Докажите теорему о проекциях отрезков.



85.

Задачи А

62. Отрезок а — проекция отрезка Ь. Всегда ли отрезок а короче Ы

63. Может ли ромб быть проекцией квадрата? А трапеции?

64. Существует ли неплоская фигура, проекция которой — отрезок?

65. Треугольник А1В1С1 — проекция треугольника АВС. Постройте
проекции средних линий треугольника АВС.

66. Треугольник А1В1С1 —- проекция треугольника АВС. Постройте
проекции медиан треугольника АВС.

67. Может ли сечением куба быть треугольник, правильный треуголь­
ник, прямоугольник, квадрат, трапеция?

68. Точка К — середина ребра АО тетраэдра АВСВ. Постройте сече­
ние тетраэдра плоскостью, проходящей через точки В, С и. К.

В

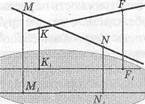
Рис. 29

69. Может ли неравнобедренная
трапеция быть проекцией равно­
бедренной трапеции? А наоборот?


70. Пересекаются ли прямые МЫ и
КР, изображенные на рисунке 29, если
М1Ы1 и К1Р1 — их проекции на
плоскость а?

71. Нарисуйте произвольную трапе­
цию А1В1С1В1 Пусть она — проекция
некоторой равнобедренной трапеции

АВСВ. Постройте проекцию высоты этой трапеции, проведенной из вершины В.

72. Точка М — середина ребра СВ тетраэдра АВСВ. Постройте сече­
ние тетраэдра плоскостью, проходящей через прямую АВ и
точку М.

73. Точки К, Р, Т — середины трех ребер, выходящих из одной
вершины тетраэдра. Построить сечение тетраэдра плоскостью,
проходящей через точки К, Р, Т.

С

74. Какой фигурой может быть проекция прямого угла?

75. Точки К, Р, Т лежат на трех ребрах, не выходящих из одной
вершины тетраэдра. Постройте сечение тетраэдра плоскостью,
проходящей через точки К, Р, Т.

76. Точки К, Р, Т — середины трех скрещивающихся ребер куба.
Постройте сечение куба плоскостью, проходящей через точки К,
Р,Т.


7 7. Четырехугольник А^С, Вх — проекция параллелограмма АВСВ.

Если: 1) \АА1\ = 2 м, \ВВ\\ = 3 м, \ССг\ = 8 м;

2) \АА.1\ = а, |ББХ| = Ь, \ССг\ = с, то найдите длину отрезка ВВг.

Дополнительные задачи

Плоскость Р пересекает прямую а, параллельную плоскости а. Докажите, что плоскости ри а пересекаются, а || а, прямая Ъ пересекает прямую а. Каким может быть взаимное расположение прямой Ъ и плоскости а?

Дано: а 11 а, а 11 р, Ъ 11 а, Ь 11 р. Каким должно быть взаимное распо­ложение данных прямых, чтобы плоскости аир были парал­лельны?

Трапеция АВСВ ([АВ] 11 [СВ]) служит изображением равно­бедренной трапеции А1В1С1В1, углы при основании которой равны 45°. Постройте изображение центра окружности, описанной вокруг трапеции.

Трапеция АВСВ ([АВ] 11 [СВ]) служит изображением прямоуголь­ной трапеции А^В^В^ имеющей угол Бр равный 60°. Известно, что в данную трапецию можно вписать окружность. Постройте центр этой окружности.

Треугольник АВС служит изображением прямоугольного треугольника А^С., у которого АСг= 90° и \АгС^: ЩС^ = 3:1. Постройте изображение высоты треугольника, проведенное из вершины прямого угла.

Треугольник АВС служит изображением равнобедренного треугольника А1В1С1, у которого \А^С^ = \ВгС^ и высота равна основанию. Постройте изображение: 1) центра описанной окружности; 2) центра вписанной окружности. Параллелограмм АВСВ служит изображением квадрата А1В%С1ВГ Постройте изображение: перпендикуляра, проведенного из точки М1(М1 е [ОД]) к прямой: 1) ЩД); 2) (В Я), где Е1 — середина

86. Через вершину квадрата проведена плоскость а, параллельная его диагонали. Докажите, что изображением квадрата в плоскости а будет параллелограмм.

 

78. 79.
81.
82.
 

 


 



 


26


 


ТЕСТОВЫЕ ЗАДАНИЯ К ТЕМЕ "ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ"

ТЕСТЫ 1,1

1. Найдите среди обозначенных
символами предложений
правильное:

>/

а) М=апЬ, аса, Мйа; Ь)аса, Ъса,К=апЬ; с)аса,Ьса, М=--а п Ь; й) М=а п&,йса, Ке. а; е)аса, Ь = опа.

2. Найдите правильное обозна­
чение:

а) и г, р = О;

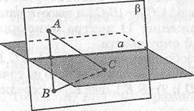
3. АВС— треугольник. А.ВеР, С е а, С ё а, а = а п Р. Найдите правильный ответ:

а)[АС}па = Х1; Ь)(ВС)па = Х2;

й)ас {ЛВС); е)Веа, аса.

4. аI! & I! а, где а — плоскость. Най­дите правильный ответ:

а) (СО) = (ОМ); Ъ) (СП) | а; с) (ОМ) 1 &; й) (СМ) 1 а; е)М€(СО).


 


■


Если а и 6 — скрещивающиеся прямые, тогда они:

а) не пересекаются и параллельные;

Ъ) не пересекаются и лежат в одной плоскости;

с) пересекаются и не лежат в одной плоскости;

й) не лежат в одной плоскости и не имеют общих точек;

е) не лежат в одной плоскости и параллельны.

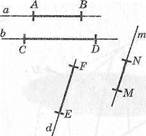
а || Ь, 4 |! т. Найдите правильный ответ:

Ь)[ЕЩ\\{МтНСЩ

с) [АВ] || {СО], {ЕР] || 1МЩ;

 

а)а\\Ь\\т;

е)аЩй.

Найдите правильное обозначение: а)а\\с, й\\с =» а\\Ъ; Ъ)а\\с, с\\&, Ъ%(1 =$ а\\Ф, с)а\\с, Ъ\\д,=$а\\Ф, й)а\\Ъ, Ъ\\с, с\\а =>а\\Ф, е)а\\Ъ, Ыс

 
 
 
: {^

АВСО — параллелограмм. А, В е а. Найдите правильный ответ:

 

 

а) [АО] с а;  
Ъ) [ВС] - с а;  
с)[ВС]< з а;  
а) ЮС] На;  
е)[АС]\ | а.  
а\\Ь\\с, |АС| 5. |АА|
(св.| 3 ' \Сфг\
а) 3:2;    
Ь) 3: 5;    
с) 5: 3;    
й) 1:3;    
е)5:2.    






м

В

,С

7.
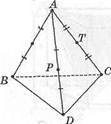
Какая фигура образуется при пересе­чении тетраэдра с плоскостью (КРТ)? к а) треугольник; Ь) четырехугольник; с) пятиугольник; Л) ромб; е) квадрат.

 

28


 

     
у' в в,
м

В


10. Найдите правильный ответ. А8С1)А1Б1С11)1 - куб.

а) АВ и ОС — скрещивающиеся прямые;

Ъ)(АВ)\\(А1В1)\\(В1С1); с)(АВ)\\{А1В1)\\{СС1);

й) ААг и ВС — нескрещивающиеся прямые;

|| (ВО.

Тесты 1.2

1.

|АГ1^\Г1| = 2,6 см, \МЩ —? а) 3,6; *; 6,2;

4) 4,2;

е) 8,2.

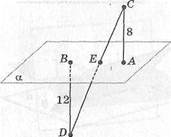
|АС| = 8, [ОС] п а,

2. А, В е а, [АС]
\ВО\ = 12, |АВ[ = 6;
|АЕ|-?

а) 2,4; Ъ) 2,2; с) 1,8; й) 1,6; е; 1,4.

 

3. |АС|:|СВ| = 4:3,

а; 2: 3; &; 1: 2; с; 2: 1; й; 4: 3;

е) 3:4.


,), 1ВВ.И

4. Аео,|АС| = |СВ|,(ОС1)|

=12 см, \ССг\ —?

а;3; Ъ)4; с) 5;

в; 8.'

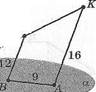
5. А,Веа,[АК]Ц[ВМ],|АК|=16,|МВ| =
= 12, |АВ| = 9, С= (МЖ) п а, |АС| -?

а; 24; Ь)28; с) 32;

6.

а — плоскость, АВС — треугольник.

\АК\=\КВ\ \АР\ = \РС\ ®АВС____ 9

^ АКР

а) 2:1;

6; 1: 2; с^) 1:4;

е) 2: 3.

Какое из них правильное?

 
 

а) О е а;

Ь)Сф,

с) (АВ) и (СО) — скрещивающиеся прямые;

Л) (АВ) и (СО) — параллельные пря­мые;

е) (АВ)ж(СО) —пересекающиесяпря- *^ мые.


■


■• с в^

И


 







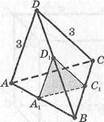
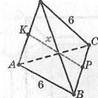
7. Ребро правильного тетраэдра равно 3 см. А1,1)1,С1— средние точки.

, ' 7-УЗ

Ив'

16 '

4'

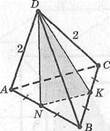
8. Ребро правильного тетраэдра равно 2 см. М, К — середины ребер АВ, ВС. Вшк —?

а)-4-; &;т,

4 '

,, л/13.

4 '

9. Ребро правильного тетраэдра равно 4 см.

\ВР\ = \РС\. 8ВАР~? а>» 4;

Ь) 2Л; с; зУг; й)

е)

10. Ребро правильного тетраэдра равно 6 см. Р, К — середины противоположных ребер. \РК\ — 1

а) Ъ) 2Д; с) 5У2; й) 2Д; е) бД.

а)
с)

 


Глаза Ш. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

§11. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ

Введем сначала понятие "угол между прямыми в пространстве". Если две пересекающиеся прямые образуют прямые углы, то говорят, что угол между этими прямыми равен 90°. Если пересекающиеся прямые образуют острые и тупые углы, то за угол между данными прямыми принимается мера острого угла.

Определение. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными данным скрещивающимся.

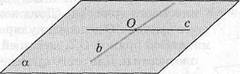
На рисунке 30 ашЬ — скрещивающиеся, а с и а — параллельные прямые. Прямые & и с лежат в одной плоскости и пересекаются. По определению для угла между скрещивающимися прямыми а и Ъ берется угол между пересекающимися прямыми с и Ъ, т. е. /.(а, Ъ) = "ЛЬ, с).

Замечание. Так как в пространстве две прямые не всегда пересекаются, угол между прямыми — не угол, не фигура, а угловая мера, величина.

Определение. Две прямые в пространстве называются перпен­дикулярными, если угол между ними равен 90°.

Итак, в пространстве прямые могут быть перпендикулярны­ми, пересекающимися и скрещивающимися. Например, если АВСОА1В1С1В1 — куб, то каждая из прямых ВС, НС, АВ, А1 Бх, А1В1 перпендикулярна к прямой ССг (рис. 31).

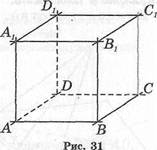
Рис. 30

Отрезки (лучи) называют перпендикулярными, если они принадлежат перпендикулярным прямым.

Теорема 13. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямой.

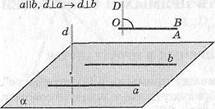
Доказательство. Пусть а \\ Ъ и й 1. а. Докажем, что <И- Ъ (рис. 32).



       
   
 
 

Рис, 32

Для этого через какую-нибудь точку О проведем прямые ОА, ОВ и ОВ, соответственно парал­лельные прямым а, Ъ и й. Так как а || Ь, то прямые ОА и ОВ совпа­дут, т.е. /.ВОВ =/ВОА. Но по ус­ловию й!. а (/ВОА = 90°), поэто­му /ВОВ = 90°. А это значит, что й X Ь. Теорема доказана.

§12. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

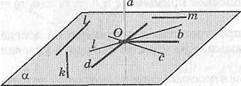
Определение. Прямая называется перпендикулярной к плос­кости, если онаперпендикулярна клюбойпрямой, лежащей в плоскости, проходящей через точку пересечения.

В этом случае и плоскость будет перпендикулярна к пря­мой: а± а и аХ а (рис. 33).

Рис. 33

Отрезок (луч) называется перпендикулярным к плоскос­ти, если он лежит на прямой, перпендикулярной к данной плоскости.

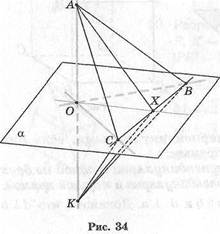
Теорема 14 (признак перпендикулярности прямой и плоскости). Если прямая, пере­секающая плоскость, перпендикулярна к двум прямым этой плоскости, проходящим через точку пересечения, то она перпен­ дикулярна к плоскости.

Доказательство. Пусть прямая АО, пересекающая плос­кость а в точке О, перпендику­лярна к прямым ОВ и ОС этой плоскости (рис. 34). Докажем, что прямая АО перпендикулярна к любой прямой ОХ, лежащей в плоскости а. Для этого проведем произвольную прямую, пересе­кающую прямые ОВ, ОС и ОХ в точках В, С и X. А на прямой ОА в разные стороны от О отложим равные отрезки ОА и ОК. Сое­динив отрезками точки А и К с точками В, С, X, получим не­сколько пар треугольников. Тре­угольники АВК и АСК равно- бедренные, так как их медианы


 

ВО и СО являются и высотами. Значит, |АВ| = \ВК], \АС\ = \СК\ и треугольники АВС и ВСК равны по трем сторонам, поэтому /.АВС = = /КВС. Равны и треугольники АВХ и КВХпо двум сторонам и углу между ними. Следовательно, \АХ\ = \КХ.\. Так как треугольник АХК— равнобедренный, то его медиана ХО является и высотой, т.е. (АО) X (ХО). А это значит, согласно определению, прямая ОА перпен­дикулярна к плоскости а. Теорема доказана.

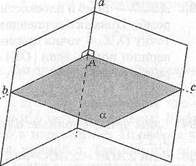
Задача 1. Через данную точку

прямой провести перпенди­кулярную ей плоскость.

Рис.

Решение. Пусть а — данная прямая и А— точка на ней (рис. 35). Проведем через прямую а две плос­кости. Проведем в этих плоскостях через точку А прямые Ъ же, перпен­дикулярные к прямой а. Плоскость, проходящая через эти прямые, перпендикулярна к прямой а по теореме 14.

Вопросы и задания

1. Что называется углом между скрещивающимися прямыми?

2. Какие прямые в пространстве называются перпендикулярными?

3. Верно ли утверждение, что "перпендикулярные прямые лежат в одной плос­
кости"?

4. В каких условиях прямая перпендикулярна к плоскости?

5. Прямая а перпендикулярна к плоскости а. Могут ли существовать в плоскости
прямые, не перпендикулярные к прямой а?

6. Докажите теорему о признаке перпендикулярности прямой и плоскости.

7. В каких условиях отрезок (луч) перпендикулярен к плоскости?

8. В окружающей обстановке найдите примеры взаимно перпендикулярных пря­
мых и прямой, перпендикулярной к плоскости.

А

87. АВСОА1В1С1В1 — куб. Найдите угол между прямыми ВВ1 и АО,.

88. АВСВА1В1С1В1 — куб. Найдите угол между скрещивающимися
прямыми АВХ и В^С.

89. Сколько прямых, перпендикулярных к данной прямой, можно
провести через данную на этой прямой точку? А через точку, не
лежащую на данной прямой?

90. Даны плоскость а и параллельная ей прямая а. Сколько прямых,
перпендикулярных к прямой а, можно провести в плоскости а?


Ыа, а±а -> а\\Ь 1Л

91. 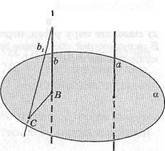й1йиО = апа. Точки АжВ лежат на прямой а. С ж В — точки
плоскости а. Докажите, что если \ОС\ = \ОВ\, то \ВС\=\ВВ\.

92. ЛВСВ — квадрат в плоскости а, его диагонали пересекаются в
точке О. Прямая а проходит через точку О и перпендикулярна к
плоскости а. Точка Е лежит на прямой а. Длина диагонали
квадрата равна 6 см, а \ОЕ\ = 4 см. Найдите расстояние от точки Е
 до вершин квадрата.

93. АВСВ — ромб в плоскости а. О — точка пересечения диагоналей
ромба. Прямая й перпендикулярна к плоскости а и проходит через
точку О. Е — точка прямой а\ Найдите расстояние от точки.Едо
вершин ромба, если | ОЕ | = 8 см, | АВ \ = 12 см и один из углов
ромба равен 60°.

В

94. Даны четыре прямые: с1\\ д,г и 1\\ 1Г Докажите, что если 61.1, то

агир

95. Если /ЛОВ = /АОС=50°, то могут ли быть перпендикулярными
прямые ОВ и ОС?

96. Лучи ОА, ОВ и ОС попарно перпендикулярны. Найдите периметр
треугольника АВС, если: а) \ОА\ = \ОВ\ = \ОС\ = 5 см; б) \ОА\ = \ОВ\ =
= \ОС\ = а; в) \ОА\ = \ОВ\ = 3 дм, \ОС\ = 4 дм.

97. Существует ли замкнутая неплоская ломаная из пяти звеньев,
каждое звено которой перпендикулярно смежному?

С

98. В правильном тетраэдре АВСВ середины сторон АВ и СВ обо­
значены через Е и К Докажите, что (ЕЕ) ± (АВ) и (ЕР) ± (СВ). Если
\АВ\ = 4 см, то найдите длину отрезка ЕР.

99. Если /МОМ = 30°, /.МОЕ = 40°, то могут ли быть перпендику­
лярными прямые (Ж и ОШ

§13. СВОЙСТВА ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ

Теорема 15. Если плоскость перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

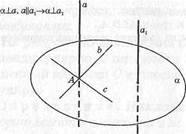
Доказательство. Пусть а \\ аг и а _1_ а. Докажем, что аг _1_ ос (рис. 86). Так как а Л а, то в плоскости а найдутся пересекающиеся в точке А прямые бис, перпендикулярные а (по определению). Так как Ьжс перпендикулярны к прямой а, то по теореме 13 они перпен­дикулярны и к прямой ах, параллельной а. Поэтому по теореме 14 аг 1. а. Теорема доказана.


Рис. 37

Рис. 36

Теорема 16 (обратная теорема). Две прямые, перпендикулярные к одной плоскости, параллельны.

Доказательство. Пусть а±а и Ъ ± а. Докажем, что а || Ь (рис. 37). Допустим, что прямые а и Ъ не параллельны. Выберем на прямой Ъ точку В, не лежащую в плоскости а. Проведем через точку В прямую Ъг, параллельную прямой а. Так как а 1 а, то и Ъх _1_ а (по теореме 15). Если В ж С — точки пересечения прямых ЬшЬ1 с плоскостью а, то из предположения следует, что в треугольнике ВВС два прямых угла. Этого не может быть. Значит, прямые ажЪ парал­лельны. Теорема доказана.

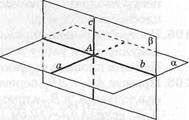
Задача 2. Через точку А данной плоскости а провести перпен­дикулярную ей прямую.

Рис. 38

Решение. В плоскости а через точку А проведем прямую а (рис. 38). Через точку А проведем плоскость Д перпендикулярную к прямой а (зада­ча 1). Пусть а п (3 = Ъ. В плоскости {3 через точку А проведем прямую с, перпендикулярную прямой Ъ. Отсюда с ± Ъ и с ± а. По признаку перпендикулярности прямой и плоскости (теорема 14) с ± а. Итак, с — искомая прямая. Методом от противного можно доказать и единственность этой прямой.

А________ С

я-------------------- 7> '

Вопросы и задания

1. Докажите (теорему), что если плоскость перпен­
дикулярна одной из двух параллельных прямых, то
она перпендикулярна и к другой.

2. Докажите (теорему), что две прямые, перпендику­
лярные одной и той же плоскости, параллельны.

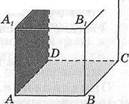
3. На рисунке 39 изображен прямоугольный парал­
лелепипед. Используя рисунок, ответьте на вопросы: Рис. 39


 




1) К каким ребрам перпендикулярно основание АВСВ?

2) Назовите пару ребер, перпендикулярных к грани АВВхАг.

4. В окружающей обстановке найдите примеры на свойства перпендикулярности прямой и плоскости.

Задачи

100. Сколько прямых, перпендикулярных к данной плоскости, можно
провести через данную точку? А отрезков?

101. а ± а. Как расположены относительно плоскости а прямые, пер­
пендикулярные к прямой а?

102. Постройте сечение куба плоскостью, проходящей через середину
его ребра перпендикулярно к этому ребру. Найдите площадь
сечения, если ребро куба равно 3 см.

103. Плоскость а перпендикулярна к катету МК прямоугольного тре­
угольника МЫК и делит его в отношении \ММг\: \МгЩ = 3:2.
В каком отношении плоскость а делит гипотенузу ММ?

В

104. Расстояния от точки Р до всех вершин квадрата равны, точка О —
центр квадрата. Докажите, что прямая РО перпендикулярна к
плоскости квадрата.

105. Постройте сечение правильного тетраэдра плоскостью, перпен­
дикулярной к ребру и проходящей через середину этого ребра.
Найдите площадь сечения, если ребро тетраэдра равно 8 см.

106. Прямые ААХ и ВВг, перпендикулярные к плоскости а, пересекают
ее в точках Аг и Вг, а прямая АВ — в точке С. Найдите расстояние
А^Вг, если \АА1\ = 12 см, \ВВг\ = 4 см, 15^1 = 2 см.

107. Треугольник АВС — равносторонний, а отрезок АО перпенди­
кулярен к его плоскости. Найдите периметр и площадь треуголь­
ника ОВС, если: 1) \АВ\ = 6 см, \АО\ = 8 см; 2) \АВ\ = \АО\ = а.

 

108. Прямые ААг и ВВг, перпендикулярные к плоскости а, пересека­ют ее в точках Аг и Вр а прямая АВ — в точке С. Найдите рас­стояние ВС, если {АА^ = 12 см, ^В | = ЩВ^ = 3 см.

;

§14. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ

Определение. Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости, лежащей на прямой, перпендикулярной к плоскости.


 


Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

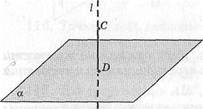
На рисунке 40 даны: точка С и плоскость а. Прямая / проведена перпендикулярно к плоскости а. Отрезок СО — перпендикуляр, опущенный из точки С к плоскости ее Точка I) — основание перпен­дикуляра.

Определение. Наклонной называют отрезок, один конец которого лежит в плоскости и не является перпендикуляром к данной плоскости (рис. 41).

Конец отрезка, лежащий в плоскости, называется основанием наклонной. А отрезок, соединяющий основание перпендикуляра и наклонной, проведенных из данной точки, называется проекцией наклонной.

На рисунке 41 изображены перпендикуляр СД проведенный из точки С к плоскости а, наклонная СИ и ее проекция ВЫ.

Длина отрезка СО на рисунках 40, 41 — расстояние от точки С до плоскости а.

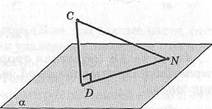
Рис.41

Рис. 40

Перпендикуляр СТ> меньше, чем наклонная СИ, т.е. | СБ | < | СЫ\. Действительно, в прямоугольном треугольнике СОИ СВ — катет, СЛ/— гипотенуза. Итак, перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из этой же точки к данной плоскости. Поэтому для расстояния от точки до плоскости дается следующее определение.

Определение. Расстоянием от точки до плоскости назы­вается длина перпендикуляра, опущенного из этой точки на плоскость.

Выше, когда говорилось о проекции наклонной, речь шла о прямоугольной проекции наклонной. Такие проекции получают при условии, что все проектирующие прямые перпендикулярны к плоскости проекций. Прямоугольное проектирование (или ортогональное проектирование) — один из видов параллельного проектирования.

В дальнейшем, говоря о проекциях, мы в основном будем иметь в виду только прямоугольные проекции.


 




§15. ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Теорема П. Прямая, проведенная на плоскости перпендикулярно

к проекции наклонной, перпендикулярна и к этой наклонной.

б)

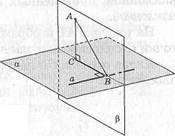Доказательство. Пусть АС — перпендикуляр к плоскости а, АВ — наклонная ж а — прямая в плоскости а, проходящая через основание наклонной В (рис. 42, а). Проведем плоскость р через пересекающиеся прямые АС, ВС (теорема 2) (рис. 42, б). Прямая а перпендикулярна к плоскости |3, так как прямая а перпендикулярна к двум пересекающимся прямым АС и ВС в плоскости р (теорема 14). Следовательно, прямая а перпендикулярна к любой прямой плоскос­ти р, т.е. а 1. [АВ}. Теорема доказана.

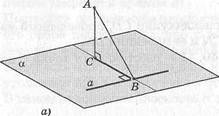
Рис. 42

Теорема 18 (обратная теорема). Если прямая на плоскости перпендикулярна к наклонной, то она перпендикулярна и к проекции наклонной.

Воспользовавшись способом доказательства прямой теоремы и рисунком 42, обратную теорему докажите самостоятельно.

Вопросы и задания

1. Что называют перпендикуляром, проведенным из точки на плоскость?

2. Что называют основанием перпендикуляра?

3. Что такое наклонная, проведенная из данной точки к плоскости?

4. Что такое проекция наклонной?

5. Что такое расстояние от точки до плоскости?

в. Что такое прямоугольное (ортогональное) проектирование? 7. Докажите теорему о трех перпендикулярах.

Задачи А

109. Из точки А к плоскости а проведены АА1 — перпендикуляр и АВ — наклонная. ВА1 — проекция наклонной. Найдите:

1) \ВАг\, если \АВ\ = 5 см, |АА1| ='4 см;

2) \АВ\, если \ААг\= 8 дм, \ВЩ = 6 дм;

3) \АА%\, если \АВ\ = 16 см, \ВА1\ = 4 см.


 

110. ОС — перпендикуляр к плоскости равностороннего треугольни­
ка АВС. Р — середина стороны АВ. Докажите, что [ОР] ± [АВ].

111. ВЕ — перпендикуляр к плоскости квадрата АВСВ. Найдите
расстояние от точки Е до прямых ВС, СП, АС, если \ВС\ = 3 см,
\СЕ\ = 4 см.

112. Через вершину А ромба АВСВ проведена прямая АР перпен­
дикулярно к его плоскости. Найдите расстояние от точки Р до
прямых ВС, СВ и ВВ, если \РА\ = \АВ\ = а и АБС= 120°.

В

113. Из данной точки к плоскости проведены две наклонные, равные
18 и 24 дм. Разность проекции этих наклонных 14 дм. Найдите
проекции наклонных.

114. Из точки А, отстоящей от плоскости а на расстояние 0,8 м,
проведена наклонная длиной 1 м. Какой фигурой представляется
геометрическое место точек основания наклонной?

115. Из точки к плоскости проведены две наклонные. Найдите длины
наклонных, если проекции наклонных равны 12 и 40 см: 1) их
сумма равна 56 см; 2) их отношение равно 15:41.

 

116. Точки Си В, делящие отрезок АВ на три равные части, отстоят
от плоскости на 3 и 6 см. Как удалены от плоскости точки А и В?

117. ОС — перпендикуляр к плоскости ромба АВСВ, АВСВ = 60°.
Постройте высоту ОН треугольника ОАВ.

118. Дан треугольник АВС. Через центр О описанной около треуголь­
ника окружности проведена прямая I, перпендикулярная к плос­
кости треугольника АВС. Докажите, что каждая точка прямой
/ равноудалена от точек А, В, С.

Дополнительные задачи

119. Через вершину прямого угла прямоугольного треугольника
проведена плоскость а, параллельная гипотенузе. Проекции

катетов на эту плоскость равны 8 и 473~ см. Найдите проекцию гипотенузы, если известно, что расстояние между гипотенузой и плоскостью равно 4 см.

120. Через одну из сторон ромба проведена плоскость на расстоянии
4 см от противолежащей его стороны. Проекции диагоналей
ромба на эту плоскость равны 8 и 2 см. Найдите проекции сторон.

121*. Длины сторон треугольника равны \АВ\ = \ВС\ = а, \АС\ = Ща * Ь). Его проекцией служит равносторонний треугольник. Найдите длину его сторон.


122. Стороны равнобедренного треугольника равны 17, 17 и 30 см.
Из вершины большого угла восстановлен перпендикуляр к
плоскости треугольника. Его длина равна 15 см. Найдите
расстояние от концов этого перпендикуляра до большей стороны
треугольника.

123. Дан прямоугольный треугольник с гипотенузой с и острым
углом а. Из вершины А данного угла проведен перпендикуляр
[АК] к плоскости треугольника. Найдите расстояние от точки К
 до катета, противолежащего данному углу, если известно, что
\АК\=т.

124. Точка М удалена от плоскости квадрата на 14 см, а от каждой
из его сторон — на 50 см. Найдите сторону квадрата и расстояние
от его вершин до точки М.

125. Дан треугольник со сторонами 13, 14, 15 см. Точка М удалена
от каждой из прямых, составляющих стороны треугольника,
на 5 см и проектируется на внутреннюю точку этого треугольни­
ка. Найдите расстояние от точки М до плоскости треугольника.

126. Точка М удалена от каждой вершины правильного треугольника

на "\/3 см, а от каждой стороны — на 2 см. Найдите расстояние от точки М до плоскости треугольника.

127. Дан ромб со стороной а и углом 45°. Точка М удалена от всех
прямых, на которых лежат стороны ромба, на расстояние Ъ.
 Найдите расстояние от этой точки до плоскости ромба и вершины
его тупого угла.

§16. РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ И ПЛОСКОСТЯМИ

Под расстоянием между двумя любыми геометрическими фигу­рами понимается расстояние между их ближайшими точками (если такие существуют). Поэтому, чтобы определить расстояние между прямыми и плоскостями, надо знать их ближайшие точки.

1. Расстояние между параллельными плоскостями.
Определение. Расстоянием между параллельными плоскостями
называют длину перпендикуляра, опушенного из любой точки одной
плоскости на другую (рис. 43). В самом деле, все перпендикуляры между
двумя параллельными плоскостями равны, потому что отрезки
параллельных прямых, заключенные между параллельными
плоскостями, равны (теорема 10).

Примером расстояния между параллельными плоскостями может служить высота призмы, высота потолка в комнате и т.д.

2. Расстояние между плоскостью и параллельной ей прямой.
Определение. Расстоянием между плоскостью и параллельной

ей прямой называется длина перпендикуляра, проведенного из любой точки прямой к плоскости (рис. 44).


 


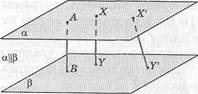
Рис. 43

Рис. 44

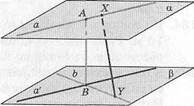
3. Расстояние между скрещивающимися прямыми. Сначала дадим понятие общего перпендикуляра скрещивающихся прямых.

Определение. Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых и перпенди­кулярный к каждой из них.

На рисунке 45 отрезок АВ — общий перпендикуляр скрещиваю­щихся прямых а и Ъ. Объясним это.

Скрещивающиеся прямые аи Ь лежат в параллельных плоскостях. Обозначим их соответственно а, р. Пусть проекция а1 прямой а на плос­кости р пересекает прямую Ъ в неко­торой точке В. Точка В является проекцией на р некоторой точки А е а.

 

Отрезок АВ будет общим перпендикуляром плоскостей а и р, а поэтому и общим перпендикуляром прямых а и Ъ. Если теперь возьмем любой другой отрезок XV (Хе а, Уе Ь), то \АВ\<\ХУ\. Поэтому расстояние между скрещивающимися прямыми связано с их общим перпен­дикуляром.

Определение. Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.

Вопросы и задания

1. Как можно найти расстояние между параллельными плоскостями?

2. Что такое расстояние между плоскостью и параллельной ей прямой?

3. Что такое общий перпендикуляр скрещивающихся прямых?

4. Как можно найти расстояние между скрещивающимися прямыми?

Задачи

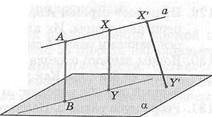
128. Расстояние между двумя параллельными плоскостями равно к. Отрезок длины а своими концами упирается в эти плоскости. Найдите проекцию отрезка на каждую из плоскостей.

а\\а
Рис. 45


 
 

§17. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

129. Из концов отрезка АВ, не пересекающего плоскость, опущены
перпендикуляры. Их длины 7 и 10 см, а расстояние между их
основаниями равно 4 см. Найдите длину АВ.

130. Концы данного отрезка, не пересекающего плоскость, удалены
от нее на 3 и 5 см. Как удалена от плоскости точка: 1) делящая
данный отрезок пополам; 2) в отношении 3: 7?

131. Ребро куба равно а. Найдите расстояние между скрещивающи­
мися диагоналями его противоположных граней.

132. Два отрезка, длины которых 13 и 37 дм, упираются концами в
две параллельные плоскости. Проекция меньшего из них на
плоскость равна 5 дм. Найдите длину проекции большего отрезка.

В

133. Отрезок длиной 10 дм пересекает плоскость, концы его удалены
от плоскости на 5 и 3 дм. Найдите длину проекции отрезка на
плоскость.

134. Из точки к плоскости проведены две наклонные, равные 17 и
10 м. Разность проекций этих наклонных равна 9 м. Найдите
расстояние от точки до плоскости.

135. К плоскости треугольника из центра вписанной в него окружнос­
ти радиусом 0,4 дм восстановлен перпендикуляр длиной 0,3 дм.
Найдите расстояние от конца этого перпендикуляра до сторон
треугольника.

136. Из вершины квадрата опущен перпендикуляр к его плоскости.
Расстояния от конца этого перпендикуляра до других вершин
квадрата равны тип (т<п). Найдите длину перпендикуляра и
сторону квадрата.

 

137. Стороны равностороннего треугольника равны 6 дм. Найдите
расстояние до плоскости треугольника от точки, которая нахо­
дится на расстоянии 4 дм от каждой из его вершин.

138. Стороны треугольника равны 2, 6,5 и 7,5 дм. Из вершины
большего угла восстановлен перпендикуляр длиной 6 дм к его
плоскости. Найти расстояние от концов перпендикуляра до
большей стороны треугольника.

139. Ребро правильного тетраэдра о. Найдите расстояние между его
противоположными ребрами.

140. Из вершины А прямоугольника АВСТ> восстановлен перпенди­
куляр АЕ к его плоскости. Найдите длину перпендикуляра АЕ,
 если его конец Е удален от вершин В, С и В на расстояния 5,11 и
10 дм.


Выше мы рассмотрели три случая расположения прямой и плоскости: 1) прямая лежит в плоскости; 2) прямая параллельна плоскости; 3) прямая перпендикулярна плоскости. Остается рассмотреть случай, когда прямая пересекает плоскость, но не перпендикулярна ей. Такие прямые могут быть наклонены к плоскости под разными углами.

Если прямая параллельна плоскости или принадлежит ей, угол между такой прямой и плоскостью считается равным 0°. Если прямая перпендикулярна плоскости, угол между ними равен 90°. В остальных случаях, чтобы определить угол, воспользуемся проекцией прямой на плоскости.

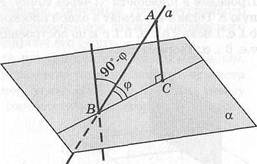
Определение. Уг­лом между прямой и плос­костью, пересекающей эту прямую и не перпендикуляр­ной к ней, называется угол между прямой и ее проекци­ей на плоскость (рис. 46).

Если ф — угол между
наклонной и плоскостью,
то 0° < ф < 90°. Угол между
прямой и плоскостью обла­
дает следующим свойством: Рис> 46
он является наименьшим

из всех углов, которые наклонная образует с прямыми, проведенными на плоскости через основание наклонной.

Это свойство докажите самостоятельно.

§18. УГОЛ МЕЖДУ ДВУМЯ ПЛОСКОСТЯМИ

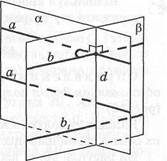
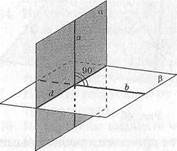
Пусть аи(3 — плоскости, пересекаю­щиеся по прямой й (рис. 47). Проведем в этих плоскостях прямые а и Ь, перпенди­кулярные й. Пусть угол между ними А(аЬ) = ф. Если в данных плоскостях про­вести какие-нибудь другие прямые, перпен­дикулярные а7, угол между ними будет такой же: ^{ахЪ^ = ф.

Рис. 47

Определение. Углом между пересе­кающимися плоскостями называется угол между прямыми, проведенными в этих плоскостях перпендикулярно линии их пересечения. Если плоскости параллельны, угол между ними считается равным 0°.


 




 


У


 


§19. Признак перпендикулярности двух плоскостей

Определение. Две плоскости называются перпендикулярными, если у гол между нимиравен 90 (рис. 48).

Теорема 19 (признак перпендикулярности плоскостей).

Если одна из двух плоскостей проходит через прямую, перпенди­кулярную к другой плоскости, то эти плоскости перпендикулярны.

Доказательство. Пусть плоскость р проходит через прямую Ъ, перпендикулярную к плоскости а. Докажем, что (5 ± а.

Прямая Ъ пересекает плоскость а в некоторой точке К (рис. 49). Эта точка — общая для плоскостей а и р. Значит, данные плоскости пересекаются по прямой с, проходящей через точку К (аксиома С4). Проведем в плоскости а через точку К прямую а, перпендикуляр­ную с. Тогда а и с лежат в одной плоскости аи Ъ _1_ а, поэтому Ъ ± а и Ы.С. Так как Ъ ± а, Ыс и по построению а ± с, то ^(сф) = /.(ао) = 90°, т.е. р ± а. Теорема доказана.

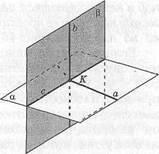
Рис. 49

Рис. 48

Теорема 20. Прямая, проведенная в одной из двух перпенди­кулярных плоскостей перпендикулярно прямой их пересечения, перпендикулярна к другой плоскости.

Используя способ доказательства теоремы 19 и рисунок 49,

докажите эту теорему самостоятельно.


⇐ Предыдущая123456789Следующая ⇒





Date: 2015-04-23; view: 14506; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.227 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию