
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема 5. Две прямые, параллельные третьей прямой, параллельны
|
|
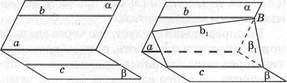
Доказательство. Пусть Ь\\ а, с\\ а (рис.12,а). Докажем, что прямые бис параллельны. Соответственно определению надо доказать, что: 1) & и с лежат в одной плоскости; 2) прямые & и с не пересекаются.
Предположим, что наши прямые не лежат в одной плоскости. Пусть а — плоскость, в которой лежат прямые а и Ъ, а В — плоскость, в которой лежат прямые а и с. Плоскости а и В различны (рис. 12,6). Отметим на прямой Ъ какую-нибудь точку Б и проведем плоскость В1 через прямую с и точку В. Она пересечет плоскость а по прямой Ьг (рис. 12,в).


 а)
а)

|
| Рис.11 |
|
| б) Рис. 12 |
| в) |
| - |
Прямая Ъх не пересекает плоскость В. Если предположим, что пересекает, то точка пересечения должна принадлежать прямой а, так как прямые &] и а лежат в плоскости а. С другой стороны, она должна лежать и на прямой с, так как она будет общей точкой плоскостей Р^ В (потому что по построению с — общая прямая плоскостей В2, В). Но это невозможно, так как прямые аи с параллельны. Значит, прямая Ъг не пересекает плоскость В.
Так как прямая Ъх лежит в плоскости а и не пересекает прямую а, то она параллельна а, а значит, совпадает с Ь по аксиоме параллельных прямых. Таким образом, прямая Ъ, совпадая с прямой 61, лежит в одной плоскости с прямой с (в плоскости В:) и не пересекает ее. Значит, прямые Ъпс параллельны. Теорема доказана.
Вопросы и задания
| 1. 2. 3. 4. |
Какие прямые называются скрещивающимися?
Какие прямые в пространстве называются параллельными?
Что можно сказать об отрезках, принадлежащих параллельным прямым?
Дан куб АВСБА^С^:
а) Укажите и обозначьте параллельные ребра куба. Сколько в кубе ребер,
параллельных одному ребру?
б) Укажите ребра, которые лежат на скрещивающихся прямых. Сколько ребер
скрещиваются с одним ребром? Обозначьте.
Докажите, что через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну. Объясните теорему о трех параллельных прямых в пространстве.
Задачи
21. Прямые ашЪ параллельны, а & и с не параллельны. Докажите,
что прямые а ж с не параллельны.
22. Отрезки ОА и ОВ пересекают плоскость а в точках Ах и Вг,
являющихся серединами этих отрезков. Найдите расстояние АВ,
если ^5^=3,8 см.
23. 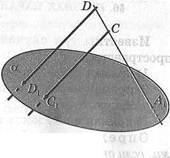 Прямые ВВХ и ССХ, изображенные на
Прямые ВВХ и ССХ, изображенные на
рисунке 13, пересекают прямую А^О
в точках 1) и С, а плоскость а — в
точках Вг и Сх. Параллельны ли
прямые ВВ1 и СС^ Если да, то почему?
24. Прямые АВ и СВ параллельны. Могут
ли быть скрещивающимися прямые
АС и ВО? А пересекающимися?
25. Прямые МЫ и ЕГ скрещиваются. Мо
гут ли быть параллельными прямые
МЕ и МТ1? А пересекающимися? Рис- 13
26.  Прямые Ъ и а" скрещиваются. Что можно сказать о прямых а и с,
Прямые Ъ и а" скрещиваются. Что можно сказать о прямых а и с,
если а\\Ътлс\\сИ
27. Прямые Ъ и искрещиваются. Как будут расположены прямые Ь
и с, если для с выполняется условие: с\\<И
28. Даны две не совпадающие параллельные прямые. Докажите, что
все прямые, пересекающие данные две прямые, лежат в одной
плоскости.
29. Прямые АВ и СО пересекаются. Докажите, что прямые АС и СО
не скрещиваются.
30. Вершины треугольника АВС —середины отрезков ОАХ, ОВХ, ОСГ
Точка О принадлежит плоскости треугольника АВС. Во сколько
раз периметр треугольника А1В1С1 больше периметра
треугольника АВС?
31. АВСОА1В1С1О1 — куб. Докажите, что плоскость треугольника
АССХ проходит через точку Ау
Теорема 6 (признактгараллелъностипрямойиплоскости). Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой в этой плоскости, то она параллельна и самой плоскости.
|
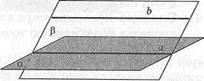
Доказательство. Пусть а — плоскость, Ъ — не лежащая в ней прямая и а — прямая в плоскости а, параллельная прямой Ъ (рис. 14, а). Проведем плоскость р через прямые Ъ и а (рис. 14, б). Плоскости аир пересекаются по прямой а. Если бы прямая Ъ пересекала плоскость а, то точка пересечения принадлежала бы прямой а.
| б) |
 а)
а)
Рис. 14
32. Из точек А и Б плоскости а проведены вне нее параллельные
отрезки: \АК\ = 18 см и \ВМ\ =12 см. Прямая МК пересекает
плоскость а в точке С. Найдите расстояние АС, если \АВ\ =9 см.
Рассмотрите оба случая.
33. Точка С делит отрезок АВ в отношении \АС\: \ВС\ = 2:3. Парал
лельные прямые, проходящие через точки А, В, С, пересекают
некоторую плоскость в точках А^В1,С1. Найдите отношение
1^1:1^1.
34. Докажите, что середины сторон пространственного четырех
угольника являются вершинами параллелограмма (вершины
пространственного четырехугольника не лежат в одной
плоскости).
35. Докажите, что если прямые АВ и СО — скрещивающиеся, то
прямые АС и ВО тоже скрещиваются.
§6. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
Известны три случая расположения прямой и плоскости в пространстве:
1) прямая лежит на плоскости;
2) прямая пересекает плоскость, т.е. прямая и плоскость имеют
одну общую точку;
3) прямая и плоскость не имеют общих точек.
Определение. Прямая и плоскость называются параллельны
ми, если они не имеют обш,их точек.
Но это невозможно, так как прямые & и а параллельны. Итак, прямая Ъ не пересекает плоскость а, а значит, параллельна плоскости а. Теорема доказана.
Теорема 7. Если плоскость (р), проходящая через прямую (&), параллельную плоскости (а), пересекает данную плоскость (а), то линия пересечения будет параллельна данной прямой (&).
Доказательство. Воспользуемся рисунком 14, б. Пусть Ъ — данная прямая, а а — линия пересечения плоскостей а и р, о которой говорится в условиях теоремы. Докажем, что а || Ь.
Допустим, что апЬ = М. Тогда точка М будет общей для прямых а и & и плоскости а, т.е. Ъ о а = М е а.
Но это невозможно, потому что по условию прямая Ъ параллельна плоскости а. Итак, а \\ Ъ. Теорема доказана.
Вопросы и задания
1. Как могут быть расположены прямая и плоскость в пространстве?
2. В каких случаях прямая и плоскость будут параллельны?
3. Повторите и запомните признак параллельности прямой и плоскости.
Докажите теорему.
4. Докажите теорему о плоскости, проходящей через прямую, параллельную
данной плоскости и пересекающую эту плоскость.
Задачи
А
36. Каждая из прямых а и Ъ параллельна плоскости а. Следует ли
отсюда параллельность прямых а и 6?
37. Прямая а параллельна прямой Ъ и Ъ || а. Следует ли отсюда, что а || а?



 38. Каждая из плоскостей аи /3 параллельна прямой а. Пересекутся ли эти плоскости?
38. Каждая из плоскостей аи /3 параллельна прямой а. Пересекутся ли эти плоскости?
В
39. Докажите, что если плоскость пересекает трапецию по ее средней
линии, то она параллельна основаниям трапеции.
40. Точки А и В лежат в плоскости а, а точка О — вне плоскости.
Докажите, что прямая, проходящая через середины отрезков ОА
и ОВ, параллельна плоскости а.
41. Сколько прямых, параллельных данной плоскости, можно
провести через данную точку?
42. Плоскость а пересекает отрезки АВ и АС посередине — в точ
ках К ж Р. Докажите, что отрезок ВС параллелен плоскости а.
Как относятся площади треугольников АВС и АКР?
43. Сколько плоскостей, параллельных данной прямой, можно про
вести через данную точку?
44. Через данную точку пространства проведите прямую, пересе
кающую каждую из двух скрещивающихся прямых. Всегда ли
это возможно?
45. Если через каждую из двух параллельных прямых проведены
плоскости, причем эти плоскости пересекаются, то линия их
пересечения параллельна каждой из данных прямых. Докажите.
46. Плоскости а и (3 пересекаются, АВСО — параллелограмм,
расположенный в плоскости а. АВЕР — равнобедренная трапеция,
расположенная в плоскости р, АВ и РЕ — основания трапеции.
Градусная мера угла АРЕ=60°. \АР] = 8 см, \АВ\ = 5 см, плоскости а
и (3 пересекаются по прямой АВ. Определите, как расположены:
1) прямые СО и ЕР; 2) прямые СО и АР; 3) найдите периметр
трапеции.
47. Даны четыре точки А,В,С,О, не лежащие в одной плоскости.
Докажите, что прямые, соединяющие середины отрезков АВ и СО,
АС и ЯД АО и ВС, пересекаются в одной точке.
48. Даны четыре точки А,В,С и Д не лежащие в одной плоскости.
Докажите, что любая плоскость, параллельная прямым АВ и СО,
пересекает прямые АС, АО, ВО и ВС в вершинах параллелограмма.
§7. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Определение. Две плоскости называются параллельными, если они не пересекаются.
|
Если плоскости а и Р параллельны, пишут: а || р.
| Рис. 15 |
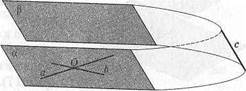
Теорема 8 (признак параллельности плоскостей). Если каждая из двух пересекающихся прямых одной плоскости параллельна другой плоскости, то эти плоскости параллельны.
Доказательство. Пусть а и Ъ — прямые в плоскости, пересекающиеся в точке О. Пусть каждая из них параллельна плоскости Р (рис.15). Докажем, что а |! р.
Будем рассуждать от противного. Пусть плоскости а и Р не параллельны, т.е. пересекаются по некоторой прямой с. По условию а \\ Р и Ь || р. Поэтому прямые а и & не пересекают с, так как прямая с лежит в плоскости р. Теперь вернемся к плоскости а. Прямые а, Ъ и с лежат в одной плоскости, а прямая с не имеет общих точек с прямыми а, Ь. Значит, а\\с, Ъ\\с. Таким образом, в плоскости а через точку О проходят две прямые, параллельные прямой с. Это противоречит аксиоме параллельных. Итак, плоскости а и Р не могут пересекаться. Следовательно, они параллельны. Теорема доказана.
Следствие. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Справедливость этого следствия прямо следует из теоремы 8.
§8. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
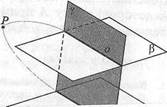
Теорема 9. Если две параллельные плоскости пересекаются
третьей, то линии их пересечения параллельны.
|
Доказательство. Пусть аир — параллельные плоскости, у — секущая плоскость, а и Ь — линии пересечения (рис. 16). Докажем, что прямые а и Ъ параллельны.
Предположим, что а и Ъ не параллельны. Тогда, так как они лежат в одной плоскости у, то пересекутся в некоторой точке Р. Точка Р принадлежит прямым а и Ъ и, значит, является общей точкой плоскостей а и р. Но это противоречит тому, что плоскости аир параллельны. Итак,
 |
|
прямые а и & не пересекаются. Значит, они параллельны. Теорема доказана.
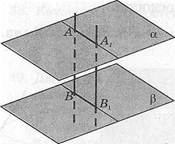
Теорема 10. Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.
| Рис. 17 |
Доказательство. Пусть отрезки АВ и А1В1 параллельны, а их концы лежат в параллельных плоскостях а и Р (рис. 17). Третья плоскость, проходящая через прямые АВ и А1Б1, пересекает параллельные плоскости аир по параллельным прямым: (ААг) \\ (ВВ^). Кроме того, по условию теоремы (АВ) || (Л1Б1). Значит, четырехугольник АВВ1А1 — параллелограмм. Следовательно, |АВ| = |А1Б1|. Теорема доказана.
Date: 2015-04-23; view: 2777; Нарушение авторских прав