
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Двугранный угол
|
|
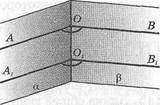
Определение. Двугранным углом называется фигура, образованная двумя полуплоскостями, ограниченными одной прямой (рис. 50).
Каждая из полуплоскостей называется гранью двугранного угла, а их общая граничная прямая — ребром.
На рисунке 50, о изображен двугранный угол. Каждая из полуплоскостей аир — грани двугранного угла, а их общая прямая а — ребро двугранного угла.
\
|
С ■ I
а)
Рис. 50
Проведем из какой-нибудь точки О ребра двугранного угла в его грани лучи О А и ВО, перпендикулярные ребру (рис. 50, б). Угол АОВ, образованный этими лучами, называют линейным углом данного двугранного угла. Другими словами, линейный угол двугранного угла — это угол, образованный пересечением данного двугранного угла с плоскостью, перпендикулярной его ребру.
Величина двугранного угла измеряется его линейным углом. Величина линейного угла двугранного угла не зависит от места вершины его на ребре. Например, углы АОВ, А1О,В1 равны между собой (рис. 50, б), потому что соответствующие стороны их параллельны и сонаправлены.
Вопросы и задания
Что называется углом между прямой и плоскостью?
Что называется углом между двумя плоскостями?
3. Какие плоскости ^называются перпендикулярными?
4. Докажите теорему о признаке перпендикулярности двух плоскостей.
5. Какую фигуру называют двугранным углом?
6. Что такое грани двугранного угла?
7. Что называется ребром двугранного угла?
8. Какой угол называется линейным углом двугранного угла?
9. Как можно получить линейный угол, пересекая двугранный угол плоскостью?
Задачи
А
141. Прямая й пересекает плоскость а под углом 45° в точке О. Можно
ли провести через точку О еще одну прямую, пересекающую
плоскость а также под углом 45°? Сколько можно провести
прямых?
142. Прямая АВ пересекает плоскость а под углом 30°. АА1 — пер
пендикуляр, а ВА1 — проекция АВ на плоскости а. Найдите:
1) |ВА1| и \ААг\, если \АВ\ = 24 см; 2) длину проекции ВА1 наклон
ной АВ, если 1АА1| = 8 см; 3) длину наклонной АВ и длину пер
пендикуляра АА1, если \ВАХ\ = 15 см.
 143. Одна из двух прямых, пересекающихся под углом 40°, перпен
143. Одна из двух прямых, пересекающихся под углом 40°, перпен
дикулярна некоторой плоскости. Докажите, что и другая прямая
пересекает эту плоскость. Найдите угол между второй прямой и
плоскостью.
144. Из одной точки к плоскости проведены две равные наклонные.
Углы между ними 60°, а между их проекциями 90°. Найдите углы
между наклонными и плоскостью.
145. Длина общей гипотенузы двух равнобедренных прямоугольных
треугольников равна 6 дм. Если плоскости треугольников перпен
дикулярны, то найдите расстояние между вершинами их прямых
углов.
146. Дан двугранный угол, мера которого 60°. Точка М, лежащая в
одной из его граней, удалена на 18 см от другой. Найдите рас
стояние от точки М до ребра двугранного угла.
147. Двугранный угол равен 45°. Точка О, лежащая на одной из
его граней, удалена от ребра на 12 см. Найдите расстояние от
точки О до другой грани.
148. Двугранный угол равен 60°. Из точки М на его ребре в гранях
проведены перпендикулярные ребру отрезки: \МЩ = 3,5 м и
\МЩ — 1,2 м. Найдите расстояние от К до N.
В
149. На какой глубине находится станция метро, если ее эскалатор
длиной 65 м наклонен к плоскости горизонта под углом 42°.
150. Отрезок длины 24 м пересекает плоскость, концы его удалены от
плоскости на 5 и 7 м. Найдите угол между прямой, соединяющей
данный отрезок с плоскостью.
151. Стороны правильного треугольника равны 12 см. Точка О,
лежащая вне плоскости треугольника, соединена с вершинами
треугольника. Все наклонные образуют с плоскостью угол,
равный 45°. Найдите расстояние от точки О до: 1) вершин;
2) сторон треугольника.
152. Квадраты АВСО и АВС1О1 лежат в плоскостях, угол между
которыми равен 60°. Найдите расстояние между их центрами,
если \АВ\ = 2а.
153. Длины перпендикуляров, опущенных из точки О на грани
двугранного угла, равны 36 дм каждый. Найдите расстояние от
точки О до ребра двугранного угла, если его мера 120°.
154. Из точек М и Годной грани острого двугранного угла опущены
перпендикуляры ММг, NN1 на другую грань и ММ2, N N2 на
ребро. Найдите длину перпендикуляра [NN21 если \ММг\ = 3 см,
\ММ2\ = 5 см, №Щ = 9 см
155. Из одной точки проведены к плоскости две наклонные, проек
ции которых равны 4,5 и 1,5 дм. Найдите длины наклонных,
если одна из них образует с плоскостью угол, в два раза больший,
чем другая наклонная.
156. Плоскости ос, (3, у попарно перпендикулярны. Докажите, что и
прямые, по которым они пересекаются, попарно перпендику
лярны.
157. Каждая из трех попарно перпендикулярных плоскостей прохо
дит через точку О. Точка А удалена от этих плоскостей на 12,
8, 9 см. Найдите расстояние ОА.
158. Сколько плоскостей, пересекающих данную плоскость под углом
40°, можно провести через данную точку?
159. Докажите, что угол между прямой и плоскостью является
наименьшим среди всех углов, образованных данной прямой с
прямыми на плоскости.
160. Аи В — точки на ребре двугранного угла меры <р, АС и ВО —
перпендикуляры к ребру, проведенные в разных гранях. Найдите
расстояние СО, если \АВ\ = а, \АС\ = Ъ, \ВО | = с.
Дополнительные задачи
161. Длина наклонной СО равна 40 дм, а длина его перпендикуля
ра ССХ составляет 20 дм. Найдите угол между прямой СО и плос
костью.
162. Если один из катетов равнобедренного прямоугольного треуголь
ника лежит в плоскости а, а другой образует с ней угол 45°,
то докажите, что угол между гипотенузой и плоскостью а со
ставляет 30°.
163. Две параллельные плоскости, расстояние между которыми 2 м,
пересекает прямая под углом 60°. Найдите длину части прямой,
ограниченной плоскостями.
164. Точка М находится на расстоянии 12 и 5 см от двух перпен
дикулярных плоскостей. Найдите расстояние от этой точки до
линии пересечения плоскостей.
165. Найдите меру двугранного угла, если расстояние от точки, взятой
на одной его грани, до другой вдвое меньше расстояния от этой
точки до ребра.
В
166. Из точки, отстоящей от плоскости на расстояние Н, проведены
две наклонные, образующие с плоскостью углы 45°, а между
собой 60°. Найдите расстояние между концами наклонных.
167. Сторона квадрата АВСВ равна 1,2 дм, точка Е находится на
расстоянии 1,2 дм от каждой из его вершин. Найдите угол между
прямой ЕВ и плоскостью квадрата.
168. Взаимно перпендикулярные плоскости аир пересекаются по
прямой I. Из точек А е а, В е В опущены [АС] _1_ / и [ВВ] ± I. Найди
те длину отрезка АВ, если: 1) \АС\ = а, \ВЦ = Ь, \СВ\ = с; 2) \АВ\ = а,
\ВС\ = Ъ, \СВ\ = с.
169. Даны плоскости а и В. а ± В и апр = й(й — прямая). В плоскос
ти а проведены а || й, а в В — плоскости Ъ \\ й. Если расстояние
между аи а1 равно 15 см, а между Ъж д, — 8 см, то найдите рас
стояние между прямыми аи Ь.
170. Плоскости квадратов МЫЕР и МЫЕ1Р1 перпендикулярны,
\МЩ = т. Найдите: 1) расстояние ЕЕХ; 2) расстояние ЕгР; 3) угол
между диагоналями МЕ и МЕу
ТЕСТОВЫЕ ЗАДАНИЯ К ТЕМЕ "ПЕРПЕНДИКУЛЯРНОСТЬ
ПРЯМЫХ И ПЛОСКОСТЕЙ"
Тесты — 2.1
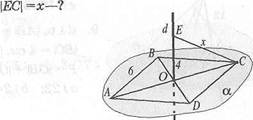
1. АВСВ — квадрат, ё±а,
\АС\ = 8 см, \ОЕ\ = 4 см, \ЕС\ =х—?
а) 2л/2;
ь; зУг;
/
.
Л) 5/2;
I ■ Г
|
171. Как через данную прямую провести плоскость, перпендику
лярную данной плоскости? Рассмотрите все возможные случаи.
172. Концы отрезка МЫ лежат на гранях двугранного угла, а рас
стояния МК и ЫР от них до ребра равны. Докажите, что
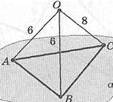
2. ОА1ОВ1 ОС, \ОА\ = |0В| =? 6 см, \0С\ = 8 см, Р = |АВ| + |ВС1 + |СА| —?
а)10/2;
с) 10
й; 20 + Зч/2; е; 10 + 4ч/2.
3. АВСГ1>А1В1С11)1— куб. Найдите угол
между прямыми АгВ и ВСГ
а) 45°;
| ■ |
&; 60°; с; 70°; Д) 80°; е>90°.
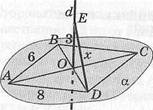
X" 4. АВОО — ромб, й±а, /ЗАВ = 60°,
1АВ| = 6см,|О^|=4см,
а; Юл/3; Ъ) М;
с) 2/Г7; й)6;
в,
| / | |||
с,
|

|
|
|
| в |
| 7. |
5. АВСБ — ромб, а ± а, ААВ-С = 120°,
\АЦ = 8 см, \ОЕ\ = 3 см, |#Д —?
^ 5; 6; 5л/2; с; 5Д; 6^8; е; 8/2.
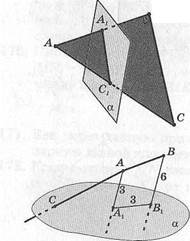
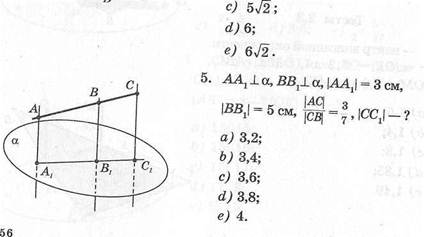
6. Л ЛВС, АВ = 90°, АВ 1а, \АА\: \АХЩ = = 7:11140^:^01?
| а) | :5; | ||
| Ъ) | 7: | :5; | |
| с) | 5: | 7; | |
| ё) | 7: | И; | |
| е) | : 7. | ||
| А/. | Ц±о;,.ВВ1_1_а,|ЯВ | х| = 6 см, | |
| !А | = 14^1 =3 см, | ||
| а) | 2; | ||
| Ъ) | 3; | ||
| с) | 4; | ||
| ё) | 5; |
е) 6.
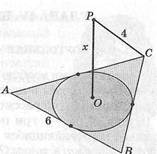
10. АБС1) — ромб, й ± а, ОЯ 1 АВ, АВСВ = 60°, \АВ\ = 8 см. |СД| —?
а)
ъ) Зл/з;
с) 4Уз; ё) бТз; е; зУ2.
Тесты 2.2
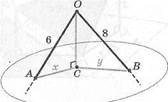
1. 0С1 а, |О4| = 6 см, \ОВ\ = 8 см.
Х-? I/-?
а; 3; 7; Ь; 7; 3;
С^ 12' 2 '
|
|
|
|
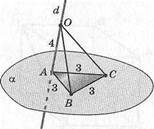
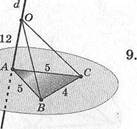
8. ААВС — равносторонний, й ± а, \АВ\ = 3 см, \АО\ = 4 см. 80вс—?
а)
0 ^;
Ю/з.
[ВС| = 4 см, \АО\ = 12 см. Р = |ОД + |ОС[ + |ВС| —? а; 22; Ь) 24; с; 26; </; 28; в; 30.
е) 3; 11.
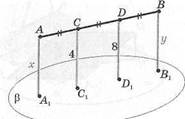
2. |АС| = \СЩ = |ДВ|, ССХ X р, ОО11 р,
| !ССХ| | = 4 см, |, | ОВ1 = 8 см, | |
| |ААХ| 1/?В | = х-? =,,__? | ||
| а) 2; | 10; | Ъ) 0; 12; | |
| с) 0; | 10; | ё) 2; 16; | е; 0; 16. |
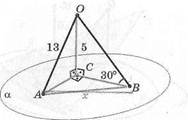
| 3. ОС± | а, 401 | ВС, | |
| \ОА\ = | = 13 см, | \ОС\ = 5 см. | |
| А.ОВС = 30°, | |4В| =? | ||
| а; ЗV | '73; | 6; л/218; | с) Зл/17; |
| 13УЗ. |
4) 27;
 |
|
|
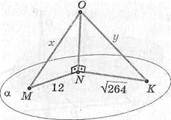
4. ОМ 1 а, \ОМ\:\ОЩ = х: у =13:17, х + у = 30 см,
\МК\ = 12 см, \МЕ\ = л/264 см, *-? у-?
а; 21; 9; &; 9; 21; с; 13;17; й; 11;19;
е) 10; 20.
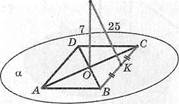
8. АВСВ — квадрат, ОМ 1 а, \ОМ\ = 7см, \МК\ = 25 см \АВ\—?\МС\—?
а,) 48; «34,6; Ь; 42; =34,6; с) 48; 35; Л) 35; 42; е; 48; «32,8.
|

|
|
|
|
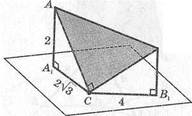
| 5. ААВС — прямоугольный, в С<=а,АВ\ |
 64
64
^ а,
= 2-УЗ см, \Вр, = 4 см, ^Ч = 2 см. |А^|—V
| с) 6; |
<г; 8; е; ю.
6. А5С1)—ромб, ДЛеа, ОС\\ а. ОВ11 а, СС1±а.
1РЩ - 2 см, 1ЖУ = 4 см, 1 = 1 см.
1 5 3
а) 9.; *;
| |; |
3;5; в/|;|?
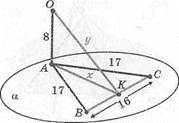
7. |АВ| = |АС| = 17 см, \ВС\ = 16 см 011а, \ОА\ ^8 см, АК1 ВС.
| а^ 15; 15; | |
| Ь) 15; 16; | |
| с) 15; 17; | |
| й; 17; 8; | |
| е) 8; 15. |
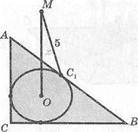
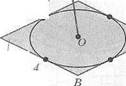
9. О — центр вписанной окружности,
ОМ± (ЛВС), \АС\ = 13 см,
С| = 14см,|АВ| = 15см,
\МСХ\ = 5 см, | ОМ\ = х --?
с; 1; Ь; 1,5; с; 2; й; 3; е; 3,5.
10. АВСО — ромб, О — центр вписанной окружности, ОМ! (АВСО) АА = 45°, \АВ\ = 4 см, \МК\ = 3 см,
а) л/7; ь; „/5; с; 273;
й; 3^/2; е) 2/5. к^
А 45
Тесты 2.3
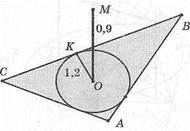
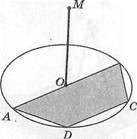
1. О — центр вписанной окружности, г = |(Ж] = 1,2 дм, ОМ'1 (АВС), \ОМ\ = 0,9 дм, \МЩ —?
^ 1,5; Ь; 1,4;
с) 1,3; й; 1,35;
е) 1,49.
|
|
|
|
|
|
|
|
| с \ |
| В |
Е
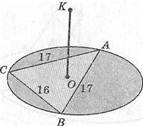
2. \АС\ = \АВ\ - 17 см, \ВС\ = 16 см. О — центр описанной окружности.
ОК1, (ЛВС), \ОЩ = 5 см, \АЩ?
5/2;
8. АВСВ— ромб.,/А - 60°, |ДО| = 4 см. О — точка пересечения диагоналехЗ. \ОЩ 2Д\А
а) 2/7;
с)
й)
е) 5У2. 4. АВСО— трапеция, \АЦ =
'I,
\АВ\ - 8 см. О — центр описанной окружности. ОМ 1 (АВСВ)
\ОМ\ = 3 см. \МС\ —? ' а) 4; Ъ) 5;
6. ААВС — равносторонний, \АВ\ = 6 см, ОР1 (ЛВС), \РС\ = 4 см, |ОЛ = х—?
а) \;
Ъ)\\
с) 1,5; (1)2; е) 2,5.
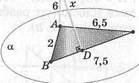
7) |АВ| = 2 см, \АС\ = 6,5 м, \ВС\ = 7,5 м.
а) 5,2; &; 5,4; с) 5,8; й; 6; е> 6,2.
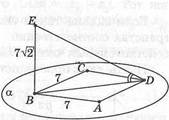
8) а || (3, \АВ\ = 17 см, |БАХ| = 8 см,
|СО| = 10/15 см, 10^1 —?
^ 23; 6,125; с) 27; ^30; е) 35.
9) АВС1) — квадрат.
\АВ\ = 7 дм.
/ВВЕ—?
а; 30°; &; 35°; с; 40°; й) 45°; е> 60°.
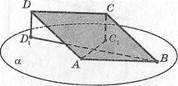
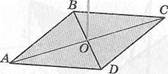
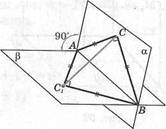
10) АВС, АВС1 — равнобедренные и прямоугольные треугольники. \АВ\ = 12 см. а 1Р.1СС,!-?
О.
 ГЛАВА IV. ВЕКТОРЫ В ПРОСТРАНСТВЕ §21. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ
ГЛАВА IV. ВЕКТОРЫ В ПРОСТРАНСТВЕ §21. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ
Координатами вообще называют числа, определяющие положение точки. Вы знакомы с прямоугольными координатами на плоскости. Аналогично можно рассмотреть систему координат и в пространстве. Пусть ос, у, г — три попарно перпендикулярные координатные прямые, пересекающиеся в точке О (рис. 51, а). Назовем их координатными осями, а точку О — главной точкой координат. Каждая ось разбивается точкой Она две полуоси — положительную, отмеченную стрелкой, и отрицательную. Каждая пара координатных осей: хшу, х л г, у я г определяют координатные плоскости (рис. 51, б). Координатные плоскости разбивают все пространство на восемь частей (октантов) (рис. 51, а).
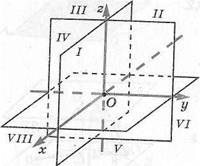
а) б)
Рис. 51
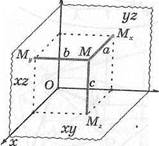
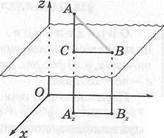
Если задана такая система координат, то каждой точке пространства соответственно можно поставить упорядоченную тройку действительных чисел, а каждой тройке чисел — единственную точку. Пусть дана пространственная точка М. Опустим из нее на плоскости у г, хг, ху перпендикуляры ММх, ММ, ММх (рис. 52). Длины этих перпендикуляров, взятые с соответствующими знаками, называют координатами точки М. В этом случае записываем: М(а, Ъ, с). Если точка лежит в какой-нибудь координатной плоскости, ее соответствующая координата равна нулю, а если на оси координат, то две координаты такой точки — нули. Например, точка N{-2,0,5!) лежит в плоскости хг, а точка К{7,0,0) — на оси Ох.

|
| У |
| Рис, 52 |
I

|
Применение метода координат в соединении с алгеброй составляет раздел геометрии, называемый аналитической геометрией. Одним из ее создателей был знаменитый французский философ и математик Рене Декарт (1596—1650). Поэтому прямоугольные координаты часто называют декартовыми.
§22. РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
1. Расстояние между двумя точками. Найдем формулу, выражающую расстояние между двумя точками А{х1;у1;г1) и В(х2;у2;г2) через координаты этих точек.
| У |
| Рис. 53 |
 Рассмотрим сначала случай, когда прямая АВ не параллельна оси Ог, как показано на рисунке 53. Проведем через точки А и В прямые, параллельные оси Ог. Они пересекут плоскость ху в точках Аг и Вг. Первая и вторая координаты этих точек такие же, как у точек А и Б, а третья координата у них равна нулю. Проведем через точку В плоскость, параллельную плоскости ху. Она пересечет прямую ААг в некоторой точке С. По теореме Пифагора АВ2 = АС2 + СВ2. Отрезки СВ и АВг равны и, как известно из планиметрии, А В 2 = {х2 - хх)2 + (у2 - уг)2, \АС\ = \г2 - гД.
Рассмотрим сначала случай, когда прямая АВ не параллельна оси Ог, как показано на рисунке 53. Проведем через точки А и В прямые, параллельные оси Ог. Они пересекут плоскость ху в точках Аг и Вг. Первая и вторая координаты этих точек такие же, как у точек А и Б, а третья координата у них равна нулю. Проведем через точку В плоскость, параллельную плоскости ху. Она пересечет прямую ААг в некоторой точке С. По теореме Пифагора АВ2 = АС2 + СВ2. Отрезки СВ и АВг равны и, как известно из планиметрии, А В 2 = {х2 - хх)2 + (у2 - уг)2, \АС\ = \г2 - гД.
Поэтому АВ2 = {х2 - хгУ + (у2 - г// + (г2 -2Х)2.
Если отрезок АВ параллелен оси Ог, то \АВ\ = \г2 - гг\. Тот же результат дает и полученная формула, так как в этом случае х% = х2, Ух = Уг
Таким образом, расстояние между точками Аи В вычисляется по формуле
 \АВ\ = л/(*2~*1 У + (У 2-У 1У + (г 2^1? (1)
\АВ\ = л/(*2~*1 У + (У 2-У 1У + (г 2^1? (1)
Эта формула часто применяется во многих разделах математики и физики.
Задача 1. Даны вершины треугольника: А(4; 4; -1), 13(7; 8; -1), С(-4; 4; -1). Вычислить периметр треугольника. Решение. Из формулы (1):
АВ2= (7 - 4)2 + (8 -4)2 + (-1 + 1)2 = 25,. АС2 = (-4 - 4)2 + (4 - 4)2 + (-1 + I)2 = 64, ВС2 = (-4 - 7)2 + (4 - 8)2 + (-1 + I)2 = 137.
Отсюда Р = 5 + 8 + л/137 = 13 + Л37.
2. Координаты середины отрезка. С помощью формулы (1) можно найти координаты середины С(х, у, г) отрезка АВ, концы которого А(хг, у1,г1)и В(х2, у2, г2):
| +. 2 |
Х="^^Я_ у=У1+У2
| (2) |
2 ' " 2
Задача 2. В задаче 1 вычислить длину медианы ВВХ. Решение.В,(1,1/,г)- середина отрезка АС. По формуле (2):
„==
| б5. |
значит, В^О, 4, -1). Отсюда
§23. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС В ПРОСТРАНСТВЕ '
Определение. Параллельным переносом, в пространстве называется такое преобразование, при котором произвольная точка (х.у.г) фигуры переходит в точку (х+ а;у + Ь; г + с), где а, Ъ, с — постоянные.
Параллельный перенос в пространстве задается формулами
х' = х + а, у' = у + Ь, г1' — г + с,
выражающими координаты (х1, у', г1) точки, в которую переходит точка (х, у, г) при параллельном переносе. Так же, как на плоскости, доказываются следующие свойства параллельного переноса.
1. Параллельный перенос есть движение.
2. При параллельном переносе точки смещаются по парал
лельным (или совпадающим) прямым на одно и то же расстояние.
3. При параллельном переносе каждая прямая переходит в
параллельную ей прямую (или в себя).
4. Каковы бы ни были точки Хж X', существует единственный
параллельный перенос, при котором точка X переходит в точку X'.
В пространстве добавляется еще одно свойство параллельного переноса.
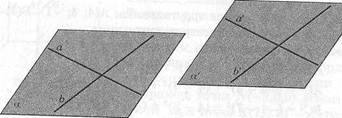
|
| Рис. 54 |
5. При параллельном переносе в пространстве каждая плоскость
переходит либо в себя, либо в параллельную ей плоскость.
Докажем последнее свойство.
Пусть а — произвольная плоскость (рис. 54). Проведем в этой плоскости две пересекающиеся прямые а и Ъ. При параллельном переносе прямые ашЬ переходят либо в себя, либо в параллельные прямые а1 и Ь1. Плоскость а переходит в некоторую плоскость а1, проходящую через прямые а1 и Ъ1. Если плоскость а1 не совпадает с а, то по теореме 8 она параллельна а. Что и требовалось доказать.
Вопросы и задания
1. Сколько координат имеет точка в пространстве?
2. Как найти координаты точки в пространстве?
3. Запишите формулу расстояния между двумя точками через координаты этих
точек. Имеет ли значение порядок точек и их координат?
4. Какими формулами определяются координаты середины отрезка?
15. Дайте определение параллельного переноса.
16. Перечислите свойства параллельного переноса.
Задачи
173. Даны точки А(1; 7; 4), Б(3; 0; 0), С(1; 2; 0), 1X0; 5; 1). Какие из этих
точек лежат: 1) в плоскости ху; 2) в плоскости у г; 3) на оси х?
174. Дана точка М(2; 4; 6). Найдите основания перпендикуляров,
опущенных из этой точки на координатные оси и координатные
плоскости.
175. Даны вершины А(1; -3; 0), В(-2; -4; 1), С(-3; 1; 1), Х>(0; 2; 0)
параллелограмма АВСО. Вычислите длины диагоналей паралле
лограмма.
176. Найдите расстояния от точки (2; -2; 3) до: 1) координатных
плоскостей; 2) осей координат; 3) начала координат.
177. Какая из точек: А(2; 1; 5) или В(-2; 1; 6) — лежит ближе к началу
координат?
178. При параллельном переносе точка А(3; 2; -1) переходит в точку
Аг(2; 0; -1). В какую точку переходит начало координат?
179. Даны точки М (0; 1; 1), Щ2; -1; 3), Щ-1; у; 0). Найдите такое
значение у, чтобы выполнялось условие: \МЩ = \ЫЩ.
180. Найдите координаты точки, лежащей на оси у и равноудаленной
от точек Р(4; -1; 3) и 0(1; 3; 0).
181. Найдите координаты точки, лежащей в плоскости ху и равно
удаленной от точек А(0; 1; 0), В(-1; 0; 1), С(0; -1; 0).
 |
182. Докажите, что четырехугольник АВСВ является ромбом, если:
А(0; 2; 0), ВЦ; 0; 0), С(2; 0; 2), В(1; 2; 2).
183. Найдите координаты вершины В параллелограмма АВСВ, если
координаты трех других его вершин известны:
АЩ 2; -1), В(1; -8; 2), С(-4; 2; 1).
184. Существует ли параллельный перенос, при котором точка А пере
ходит в точку Д а точка С —в точку В, если: А(0; 1; 2), 5(-1; 0; 1},
С(3;-2; 2), Ж2;-3; 1)?
§24. ВЕКТОРЫ В ПРОСТРАНСТВЕ
В пространстве, как и на плоскости, вектором называется направленный отрезок. Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов.
Но это не простое повторение, а обобщение, распространение свойств двумерной геометрии на трехмерную. Если в планиметрии для задания вектора достаточно указать две его координаты, то в стереометрии — три координаты.
Определение. Координатами вектора АВ, начало которого точка А{х1, ух, гх), а конец — точка В(х2, у2, гг), называются числа.
,ах = х2 — хх, п2 — у2 — ух, а.3~ г2 — гх. Записывают такой вектор, указывая его координаты: АВ(а1, а2, а3) или а (ах, а2, ав).
Например, если точки А(4; 0; 3) и 5(0; 6; 4) — начало и конец направленного отрезка АВ, тогда
^ = 0-4 =-4, а2 = 6-0 = 6, а3 = 4-3 = 1.
Значит, направленному отрезку АВ соответствует вектор а (-4; 6; 1) (рис. 55).
| 4 |
| о |
| у |
Так же, как и на плоскости, доказывается, что равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание говорить о том, что любой вектор можно отложить от любой точки пространства.
Длину вектора а (ах, а2, а8) можно выразить через его координаты. Отложим
Рис. 55
| А(а1;аг;а3) |
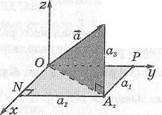 вектор а от начала координат (рис. 56). Тогда четырехугольник ОРАЫ — прямоугольник. Его стороны равны ах и а2,
вектор а от начала координат (рис. 56). Тогда четырехугольник ОРАЫ — прямоугольник. Его стороны равны ах и а2,
поэтому ОА2 = а\ + а\. В прямоугольном треугольнике ОАА второй катет \АА\=ая
Date: 2015-04-23; view: 4550; Нарушение авторских прав