Расстояние между прямыми и плоскостями

Под расстоянием между двумя любыми геометрическими фигу­рами понимается расстояние между их ближайшими точками (если такие существуют). Поэтому, чтобы определить расстояние между прямыми и плоскостями, надо знать их ближайшие точки.

1. Расстояние между параллельными плоскостями.
Определение. Расстоянием между параллельными плоскостями
называют длину перпендикуляра, опущенного из любой точки одной
плоскости на другую (рис. 43). В самом деле, все перпендикуляры между
двумя параллельными плоскостями равны, потому что отрезки
параллельных прямых, заключенные между параллельными
плоскостями, равны (теорема 10).

Примером расстояния между параллельными плоскостями может служить высота призмы, высота потолка в комнате и т.д.

2. Расстояние между плоскостью и параллельной ей прямой.
Определение. Расстоянием между плоскостью и параллельной

ей прямой называется длина перпендикуляра, проведенного из любой точки прямой к плоскости (рис. 44).

. Расстояние между скрещивающимися прямыми. Сначала дадим понятие общего перпендикуляра скрещивающихся прямых.

Определение. Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых и перпенди­кулярный к каждой из них.

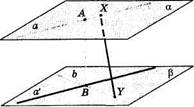
На рисунке 45 отрезок АВ — общий перпендикуляр скрещиваю­щихся прямых оиЬ. Объясним это.

Скрещивающиеся прямые аи Ъ лежат в параллельных плоскостях. Обозначим их соответственно а, р. Пусть проекция а¹ прямой а на плос­кости р пересекает прямую Ъ в неко­торой точке В. Точка В является проекцией на Р некоторой точки А е а. Отрезок АВ будет общим перпендикуляром плоскостей а и р, а поэтому и общим перпендикуляром прямых а и 6. Если теперь возьмем любой другой отрезок XY (Xea, Yeb), то |АВ|<|ХУ|. Поэтому расстояние между скрещивающимися прямыми связано с их общим перпен­дикуляром.

Определение. Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.

Вопросы и задания

1. Как можно найти расстояние между параллельными плоскостями?

2. Что такое расстояние между плоскостью и параллельной ей прямой?

3. Что такое общий перпендикуляр скрещивающихся прямых?

4. Как можно найти расстояние между скрещивающимися прямыми?

Задачи

А

128. Расстояние между двумя параллельными плоскостями равно h. Отрезок длины а своими концами упирается в эти плоскости. Найдите проекцию отрезка на каждую из плоскостей.

129. Из концов отрезка АВ, не пересекающего плоскость, опущены
перпендикуляры. Их длины 7 и 10 см, а расстояние между их
основаниями равно 4 см. Найдите длину АВ.

130. Концы данного отрезка, не пересекающего плоскость, удалены
от нее на 3 и 5 см. Как удалена от плоскости точка: 1) делящая
данный отрезок пополам; 2) в отношении 3: 7?

131. Ребро куба равно а. Найдите расстояние между скрещивающи­
мися диагоналями его противоположных граней.

132. Два отрезка, длины которых 13 и 37 дм, упираются концами в
две параллельные плоскости. Проекция меньшего из них на
плоскость равна 5 дм. Найдите длину проекции большего отрезка.

В

133. Отрезок длиной 10 дм пересекает плоскость, концы его удалены
от плоскости на 5 и 3 дм. Найдите длину проекции отрезка на
плоскость.

134. Из точки к плоскости проведены две наклонные, равные 17 и
10 м. Разность проекций этих наклонных равна 9 м. Найдите
расстояние от точки до плоскости.

13 5. К плоскости треугольника из центра вписанной в него окружнос­ти радиусом 0,4дм восстановлен перпендикуляр длиной 0,3 дм. Найдите расстояние от конца этого перпендикуляра до сторон треугольника.

136. Из вершины квадрата опущен перпендикуляр к его плоскости. Расстояния от конца этого перпендикуляра до других вершин квадрата равны тип (т<п). Найдите длину перпендикуляра и сторону квадрата.

137. Стороны равностороннего треугольника равны 6 дм. Найдите
расстояние до плоскости треугольника от точки, которая нахо­
дится на расстоянии 4 дм от каждой из его вершин.

138. Стороны треугольника равны 2, 6,5 и 7,5 дм. Из вершины
большего угла восстановлен перпендикуляр длиной 6 дм к его
плоскости. Найти расстояние от концов перпендикуляра до
большей стороны треугольника.

139. Ребро правильного тетраэдра а. Найдите расстояние между его
противоположными ребрами.

140. Из вершины А прямоугольника ABCD восстановлен перпенди­
куляр АЕ к его плоскости. Найдите длину перпендикуляра АЕ,
если его конец Е удален от вершин В, С и D на расстояния 5,11 и
10 дм.