
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Признак перпендикулярности двух плоскостей
|
|
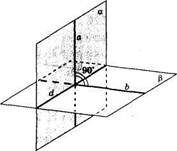
146.Определение. Две плоскости называются перпендикулярными, если у гол между нимиравен 90 (рис. 48).
147. Теорема 19 (признак перпендикулярности плоскостей).
148. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другойплоскости, то эти плоскости перпендикулярны.
149.Доказательство. Пусть плоскость Р проходит через прямую Ь, перпендикулярную к плоскости а. Докажем, что (3 X ос.
150. 
|
151.Прямая Ь пересекает плоскость а в некоторой точке К (рис. 49). Эта точка — общая для плоскостей аир. Значит, данные плоскости пересекаются по прямой с, проходящей через точку К (аксиома С4). Проведем в плоскости а через точку К прямую а, перпендикулярную с. Тогда а и с лежат в одной плоскости а и Ъ X ос, поэтому 61а и Ыс. Так как Ъ La, blc и по построению а X с, то Z(ccP) = Z(ab) = 90°, т.е. р X а. Теорема доказана.
152. 
Теорема 20. Прямаяпроведенная в одной из двух перпендикулярных плоскостей перпендикулярно прямой их пересечения, перпендикулярна к другой плоскости.
153. Используя способ доказательства теоремы 19 и рисунок 49,
Докажите эту теорему самостоятельно.
Date: 2015-04-23; view: 1480; Нарушение авторских прав