Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Для «мёртвого» зачёта всегда выполняйте проверку мысленно или на черновике!!!
|
|
Пример 4
Составить уравнение плоскости, проходящей через точки 
и начало координат.
Это пример для самостоятельного решения. Ещё раз присмотримся к формуле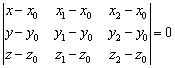 
. В каждом столбце определителя встречаются координаты точки 
, и это можно с выгодой использовать. В предложенной задаче даны три точки: , начало координат. В качестве точки можно выбрать любую из трёх точек. Подумайте, как рациональнее оформить решение! Да, и постарайтесь, не пропускать это задание, в самом конце решения увидите важный технический нюанс;-)
Вектор нормали плоскости (нормальный вектор)
Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов. Но для решения задач нам будет хватать и одного.
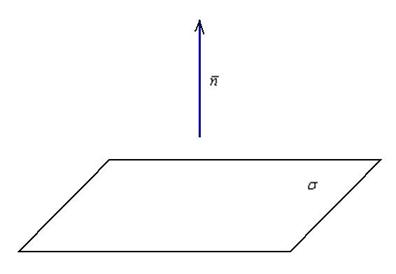
Если плоскость задана общим уравнением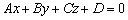
, то вектор 
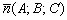является вектором нормали данной плоскости. Просто до безобразия. Всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости.
Обещанного три экрана ждут, вернёмся к Примеру №1 и выполним его проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке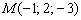 
и двум векторам 
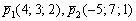. В результате решения мы получили уравнение 
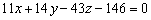. Проверяем:
Во-первых, подставим координаты точки 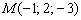в полученное уравнение:
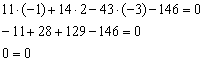
Получено верное равенство, значит, точка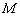 
действительно лежит в данной плоскости.
Во-вторых, из уравнения плоскости снимаем вектор нормали: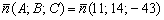 
. Поскольку векторы 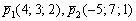параллельны плоскости, а вектор 
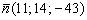перпендикулярен плоскости, то должны иметь место следующие факты: 
. Перпендикулярность векторов легко проверить с помощью скалярного произведения:
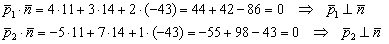
Вывод: уравнение плоскости найдено правильно.
В ходе проверки я фактически процитировал следующее утверждение теории: вектор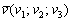
параллелен плоскости 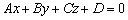в том и только том случае, когда 
.
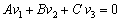Решим важную задачу, которая имеет отношение и к уроку Скалярное произведение векторов:
Пример 5
Найти единичный нормальный вектор плоскости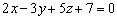 
.
Решение: Единичный вектор – это вектор, длина которого равна единице. Обозначим данный вектор через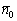 
. Принципиально пейзаж выглядит так:
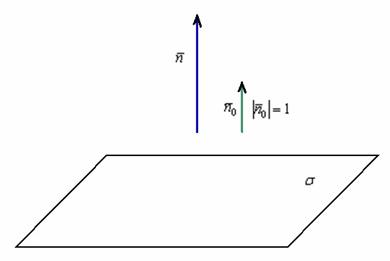
Совершенно понятно, что векторы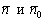 
коллинеарны.
Сначала из уравнения плоскости снимем вектор нормали: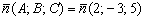 
.
Как найти единичный вектор? Для того чтобы найти единичный вектор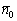, нужно каждую координату вектора 
разделить на длину вектора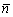 
.
Перепишем вектор нормали в виде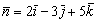 
и найдём его длину:
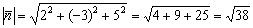
Согласно вышесказанному:
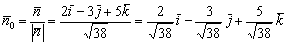
Ответ: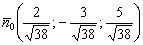 
Проверка: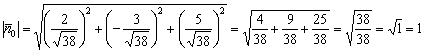 
, что и требовалось проверить.
Читатели, которые внимательно изучили последний параграф урока Скалярное произведение векторов, наверное, заметили, что координаты единичного вектора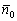
– это в точности направляющие косинусы вектора :
Отвлечёмся от разобранной задачи: когда вам дан произвольный ненулевой вектор, и по условию требуется найти его направляющие косинусы (последние задачи урока Скалярное произведение векторов), то вы, по сути, находите и единичный вектор, коллинеарный данному.
Фактически два задания в одном флаконе.
Необходимость найти единичный вектор нормали возникает в некоторых задачах математического анализа.
С выуживанием нормального вектора разобрались, теперь ответим на противоположный вопрос:
Date: 2015-04-23; view: 778; Нарушение авторских прав