Как составить уравнение плоскости по точке и двум неколлинеарным векторам?

Рассмотрим точку 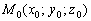и два неколлинеарных вектора 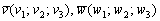. Уравнение плоскости, которая проходит через точку параллельно векторам 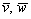, выражается формулой:

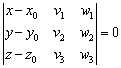
! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.

Принципиально ситуация выглядит так:

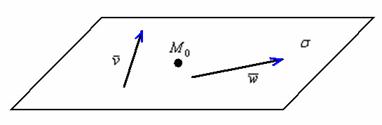
Обратите внимание, что точка и два коллинеарных вектора не определят плоскость (векторы будут свободно «вертеться» вокруг точки).

Пример 1

Составить уравнение плоскости по точке 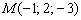и векторам .

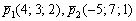Решение: Составим уравнение плоскости по точке и двум неколлинеарным векторам:

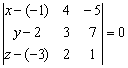
Определитель удобнее всего раскрыть по первому столбцу:

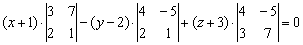
Раскрываем определители второго порядка:

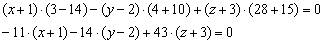
На первом месте у нас находится знак «минус». Хорошим тоном считается убрать наглеца, в этих целях меняем знак у каждого слагаемого. Проводим дальнейшие упрощения и получаем уравнение плоскости:

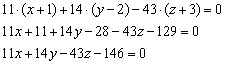
Сократить здесь ничего нельзя, поэтому:

Ответ: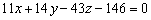

…числа, конечно, страшноваты получились для первого примера =) …но переделывать, пожалуй, не буду, на практике большие числа – вещь распространённая.

Как проверить задание? Для проверки пока не хватает информации, но я обязательно выполню её чуть позже.

Пример 2

Составить уравнение плоскости по точке 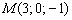и двум неколлинеарным векторам .

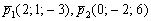Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Иногда может потребоваться решить обратную задачу – по известному уравнению плоскости найти параллельные ей векторы. Кстати, сколько параллельных векторов существует у плоскости? Бесконечно много. Однако нельзя объять необъятное, поэтому «вытащим» из уравнения плоскости три таких вектора:

Пусть плоскость задана общим уравнением 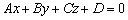. Тогда векторы 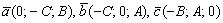будут параллельны данной плоскости (а, значит, компланарны), и какие-либо два из них – линейно независимы. Так, в Примере №1 мы составили уравнение плоскости 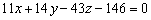. Построенной плоскости будут параллельны следующие векторы: 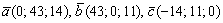. Если честно, не припомню, чтобы приходилось этим пользоваться, тем не менее, справка не лишняя.

Два неколлинеарных вектора и точка – это «жёсткая» конструкция, однозначно определяющая плоскость. Но существует более очевидный способ, о котором упоминалось выше, и он громким стуком в дверь уже давно просится на урок. Три точки. Дёшево и сердито.

Date: 2015-04-23; view: 2380; Нарушение авторских прав