
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Как построить линию в полярной системе координат?
|
|
На предыдущем уроке мы познакомились с полярными координатами, а также научились строить отдельно взятые точки и распространённые кривые в данной системе координат. Давайте подведём краткие промежуточные итоги и ответим на важный вопрос:
как построить линию в полярной системе координат?
– Сначала необходимо отметить полюс, изобразить полярную ось и указать масштаб. Кроме того, на первоначальном этапе желательно найти область определения функции, чтобы сразу же исключить из рассмотрения лишние угловые значения.
– В большинстве случаев потребуется найти десяток-другой точек, принадлежащих линии. Но иногда можно обойтись меньшим количеством, а то и вовсе отделаться схематическим чертежом.
– На следующем шаге следует прочертить угловые направления и отметить найденные точки. Как это сделать с помощью каменного топора транспортира, циркуля и линейки, я подробнейшим образом объяснил в начале статьи о полярных координатах.
– И, наконец, отложенные точки нужно аккуратно-аккуратно соединить линией (линиями).
Отработаем алгоритм построения на более основательных типовых задачах:
Пример 6
Построить по точкам линию, заданную в полярной системе координат уравнением 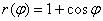 , рассматривая значения угла с интервалом в
, рассматривая значения угла с интервалом в 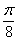 рад. Найти уравнение линии в прямоугольной системе координат.
рад. Найти уравнение линии в прямоугольной системе координат.
Решение: найдём область определения. Поскольку полярный радиус неотрицателен, то:
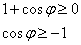
Очевидно, что условие выполнено для любого значения «фи», но, тем не менее, расскажу об удобном графическом способе решения тригонометрического неравенства: изобразите на черновике (или представьте мысленно) график функции 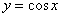 левой части неравеснтва и прямую
левой части неравеснтва и прямую 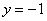 правой части неравенства. Непосредственно по чертежу видно, что синусоида расположена не ниже прямой
правой части неравенства. Непосредственно по чертежу видно, что синусоида расположена не ниже прямой 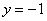 , а значит, неравенство
, а значит, неравенство 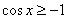 выполнено для любого значения «икс».
выполнено для любого значения «икс».
Итак, на угол 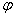 не наложено никаких ограничений, и нам предстоит «перепахать» весь круг от 0 до
не наложено никаких ограничений, и нам предстоит «перепахать» весь круг от 0 до 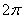 , причём, по условию сделать это требуется строго с интервалом в
, причём, по условию сделать это требуется строго с интервалом в 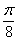 рад. (22,5 градусов). Ложку в зубы, калькулятор в руки:
рад. (22,5 градусов). Ложку в зубы, калькулятор в руки:
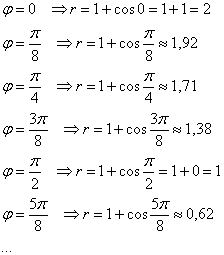
и так далее, пока не будет пройден весь оборот до «двух пи».
На практике обычно не расписывают подробные вычисления, а сразу заносят результаты в таблицу:
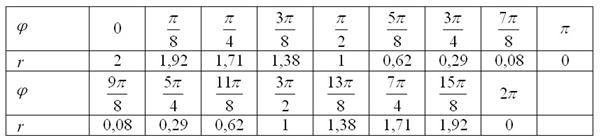
Рекомендую использовать мой расчётный макет, созданный в MS Excel, который позволит буквально в пару щелчков вычислить все значения «эр», сэкономив целый вагон времени. Программу можно закачать на странице Математические формулы и таблицы. Особо нетерпеливым читателям предлагаю также воспользоваться handmade-продуктом и быстро начертить заготовку, ориентируясь по клеточкам:
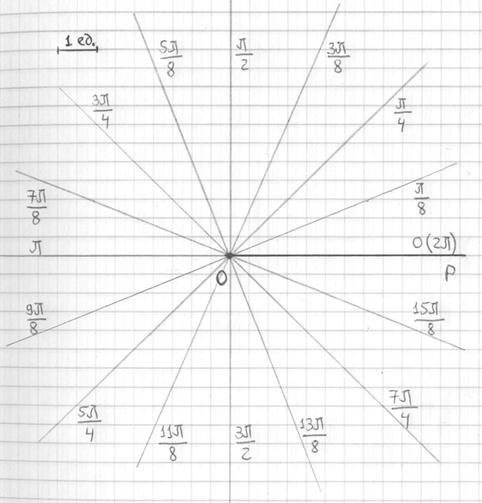
Углы проставлены для удобства и на чистовике, понятно, их записывать не надо.
…поймал себя на мысли, что уже добрые пару лет не выполнял чертежи от руки. Сейчас аккуратно извлеку тетрадь из сканера и спрячу её в укромном месте – лет через 20-30-ть продам на антикварном аукционе за 100500 золотых червонцев =) Шутки шутками, а оперативная память моего первого компьютера ZX Spectrum составляла 32 килобайта. КИЛОбайта. При этом программисты умудрялись затолкать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). Сейчас на дворе февраль 2014 года, а ведь с той поры не прошло и пары десятилетий. Боюсь, что шутливое сравнение чертёжных инструментов с каменным топором довольно скоро перестанет быть шуткой =)
После ностальгических воспоминаний отметим найденные точки на чертеже и аккуратно соединим их линией:
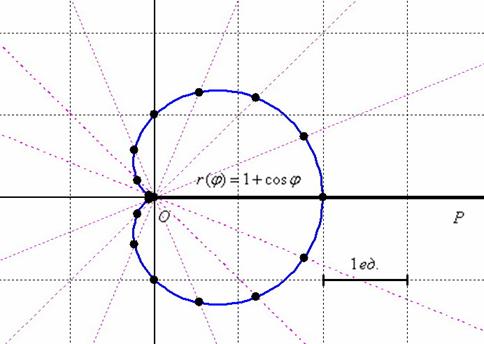
Напоминаю, что одинаковые значения радиуса эффективнее засекать циркулем, а слишком малые значения для углов 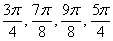 допустимо отметить и «на глазок».
допустимо отметить и «на глазок».
Найдём уравнение линии в декартовой системе координат. Для этого используем тоже уже знакомый приём – домножим обе части уравнения 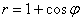 на «эр»:
на «эр»:
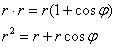
И по формулам перехода к прямоугольным координатам 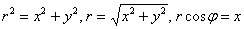 получим:
получим:
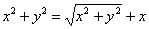
Перенесём «икс» налево и возведём обе части в квадрат:
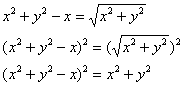
Дальнейшее возведение левой части в квадрат только усложнит запись, поэтому результат целесообразнее оставить в таком виде.
Из полученного уравнения следует, что кардиоида – это алгебраическая линия 4-го порядка, обратите внимание, насколько сложной получилась её формула по сравнению с полярной системой координат. Алгебраическим линиям 3-его, 4-го, 5-го, 6-го и высших порядков посвящены серьёзные исследования, и грибники без труда могут отыскать море информации по данной теме. Ну а я, как обычно, предлагаю вкусную и здоровую пищу на каждый день:
Пример 7
Линия задана уравнением 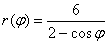 в полярной системе координат. Требуется:
в полярной системе координат. Требуется:
1) построить линию по точкам, придавая 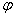 значения через интервал
значения через интервал 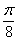 , начиная с
, начиная с 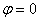 и заканчивая
и заканчивая 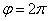 ;
;
2) найти уравнение линии в декартовой системе координат;
3) определить вид кривой.
Типовая формулировка, предвещающая час (а то и больше) усердного пыхтения, а нередко и чертыханья студента. Но только не того, кто прочитал эту и предыдущую статью о полярных координатах! Примерный образец оформления задачи в конце урока.
Рассмотрим ещё ряд важных особенностей решения:
Пример 8
Линия задана уравнением 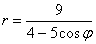 в полярной системе координат. Требуется:
в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от 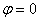 до
до 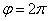 и придавая
и придавая 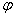 значения через промежуток
значения через промежуток 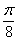 ;
;
2) найти уравнение данной линии в прямоугольной системе координат;
3) назвать линию, найти координаты фокусов и эксцентриситет.
Решение: найдём область определения:
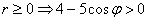
Заметьте, что ноль в знаменателе нас тоже не устраивает, поэтому неравенство становится строгим. Перенесём косинус направо и развернём избушку к лесу задом:
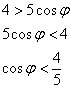
Неравенство несложно решить аналитически, но для лучшего понимания я опять воспользуюсь графическим методом. Изобразим на черновике или представим мысленно графики функций 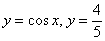 , при этом нас будет интересовать только один период – от
, при этом нас будет интересовать только один период – от 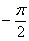 до
до 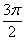 . Условию
. Условию 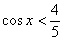 удовлетворяет та часть синусоиды, которая расположена ПОД прямой
удовлетворяет та часть синусоиды, которая расположена ПОД прямой 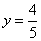 :
:
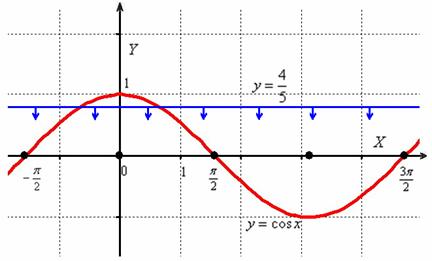
То есть, в нашем распоряжении оказываются почти все значения угла за исключением макушки, расположенной на симметричном отрезке 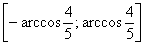 .
.
Таким образом, 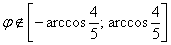 . Арккосинус
. Арккосинус 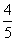 составляет примерно 37 градусов, поэтому из рассмотрения исключаем углы
составляет примерно 37 градусов, поэтому из рассмотрения исключаем углы 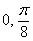 и
и 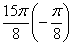 . Заполним расчётную таблицу с прочерками в соответствующих ячейках:
. Заполним расчётную таблицу с прочерками в соответствующих ячейках:
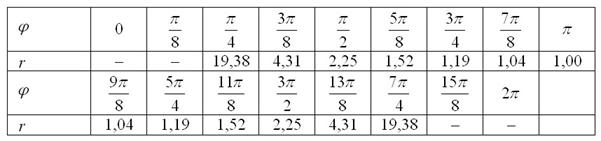
Чайники могут, в принципе, вообще не загружаться областью определения и ставить тире по факту: получилось отрицательное значение «эр» – поставили.
Выполним чертёж:
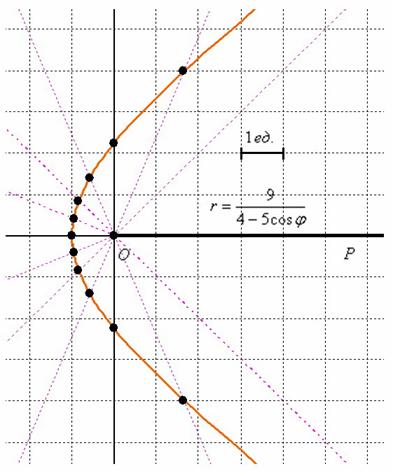
На него не вместились точки, соответствующие значениям 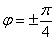 , но не уменьшать же из-за этого масштаб. Сойдёт и так.
, но не уменьшать же из-за этого масштаб. Сойдёт и так.
2) Найдём уравнение линии в прямоугольной системе координат. По всем признаком должна получиться гипербола.
Избавляемся от дроби:
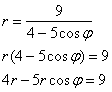
Используем формулы перехода 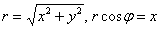 :
:
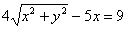
Дальнейшие действия хорошо знакомы из практикума Задачи с линиями 2-го порядка:
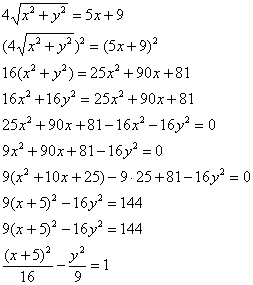
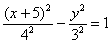 – искомое уравнение.
– искомое уравнение.
3) Данная линия представляется собой гиперболу с центром в точке 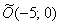 , действительной полуосью
, действительной полуосью 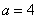 , мнимой полуосью
, мнимой полуосью 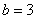 . Впрочем, формально по условию можно было и не упоминать о деталях.
. Впрочем, формально по условию можно было и не упоминать о деталях.
Вы спросите: «но в полярной же системе координат прорисовалась только одна ветвь гиперболы, поэтому не ошибочно ли говорить о целой гиперболе?». Не ошибочно!
И вот по какой причине: если подразумевать обобщённую полярную систему координат с отрицательными значениями «эр», то при значениях угла из интервала 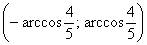 прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже противник обобщенных полярных координат, но в данном случае всё получается ловко и чертовски удобно – можно как бы и не оговариваться о том, что на чертеже только одна ветвь гиперболы.
прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже противник обобщенных полярных координат, но в данном случае всё получается ловко и чертовски удобно – можно как бы и не оговариваться о том, что на чертеже только одна ветвь гиперболы.
Вычислим координаты фокусов и эксцентриситет. По условию уравнение не нужно приводить к каноническому виду, а значит, требуемые вещи проще найти напрямую – с учётом параллельного переноса гиперболы, к тому же, она не повёрнута.
Вычислим значение 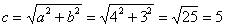 и поправкой на параллельный перенос в точку
и поправкой на параллельный перенос в точку 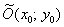 найдём фокусы:
найдём фокусы:
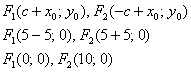
Эксцентриситет: 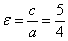
Готово.
Педантичные люди могут ещё записать развёрнутый ответ.
Заключительное задание для самостоятельного решения:
Пример 9
Линия задана уравнением 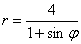 в полярной системе координат. Требуется:
в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от 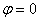 до
до 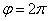 и придавая
и придавая 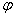 значения через промежуток
значения через промежуток 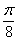 ;
;
2) найти уравнение данной линии в прямоугольной системе координат и определить её вид.
3) Привести уравнение к каноническому виду и выполнить чертёж в прямоугольной системе координат. Найти фокусы кривой и её эксцентриситет.
Внимательно проанализируйте, что и в каком порядке требуется выполнить по условию. Сам много раз налетал – краем глаза показалось одно, а нужно совсем другое. В образце решения приведение уравнения линии 2-го порядка к каноническому виду выполнено академическим способом.
На основе полярных координат плоскости базируются цилиндрические и сферические координаты пространства. В частности, угловые величины широко используются в навигации (не зря упоминались лётчики и самолёты) и астрономии. Действительно, представьте земной шар (а если строго, эллипсоид), эллиптические орбиты планет и вы поймёте, что распиаренная прямоугольная система координат как-то здесь совсем не в тему. Ну а мне пора плотно прикрыть дверь аналитической геометрии и вернуться к матанализу, где полярные координаты тоже эксплуатируются на полную катушку.
До скорых встреч!
Решения и ответы:
Пример 7: Решение: 1) Найдём область определения функции:
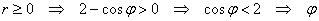 – любое.
– любое.
Заполним таблицу требуемыми значениями угла и соответствующими значениями полярного радиуса:
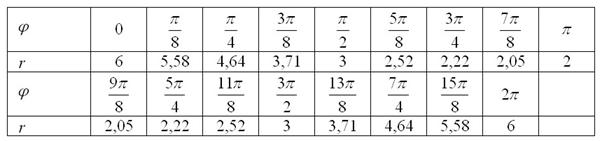
Выполним чертёж:
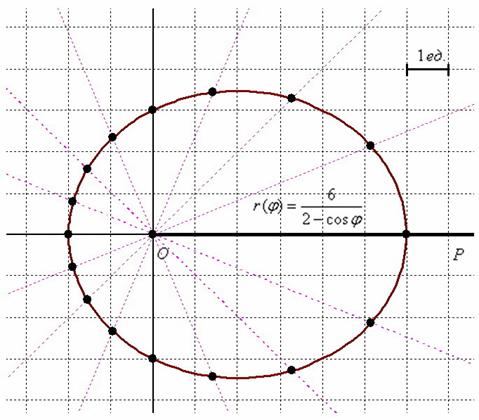
2) Найдём уравнение линии в декартовой системе координат:
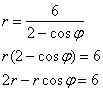
Используем формулы 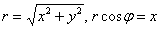 :
:
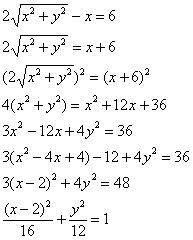
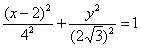 – уравнение линии в прямоугольной системе координат.
– уравнение линии в прямоугольной системе координат.
3) Данная кривая представляет собой эллипс с центром симметрии в точке 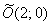 , большой полуосью
, большой полуосью 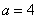 и малой полуосью
и малой полуосью 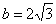 .
.
Пример 9: Решение: 1) Найдём область определения функции:
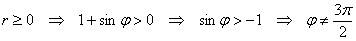
Заполним расчётную таблицу:
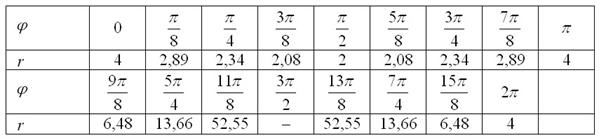
Выполним чертёж:
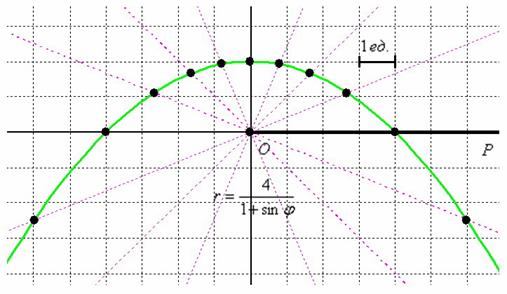
2) Найдём уравнение линии в декартовой системе координат:

Используем формулы 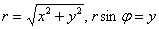 :
:
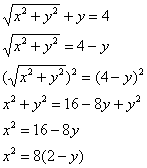
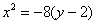 – искомое уравнение. Это парабола.
– искомое уравнение. Это парабола.
3) Приведём уравнение линии к каноническому виду с помощью перехода к новой системе координат 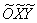 , которая получается путём поворота исходной системы координат
, которая получается путём поворота исходной системы координат 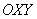 на
на 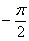 рад. вокруг точки
рад. вокруг точки 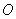 и её параллельным переносом центром в точку
и её параллельным переносом центром в точку 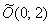 (координаты – в старой системе координат).
(координаты – в старой системе координат).
В результате получено каноническое уравнение параболы 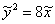 , фокальный параметр которой равен
, фокальный параметр которой равен 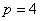 . Выполним чертёж:
. Выполним чертёж:
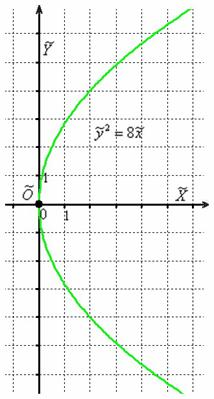
Найдём фокус: 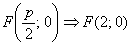 .
.
Эксцентриситет любой параболы равен единице.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Уравнение плоскости. Как составить уравнение плоскости?
Взаимное расположение плоскостей. Задачи
Пространственная геометрия не намного сложнее «плоской» геометрии, и наши полёты в пространстве начинаются с данной статьи. Для усвоения темы необходимо хорошо разобраться в векторах, кроме того, желательно быть знакомым с геометрией плоскости – будет много похожего, много аналогий, поэтому информация переварится значительно лучше. В серии моих уроков 2D-мир открывается статьёй Уравнение прямой на плоскости. Но сейчас Бэтмен сошёл с плоского экрана телевизора и стартует с космодрома Байконур.
Начнём с чертежей и обозначений. Схематически плоскость можно нарисовать в виде параллелограмма, что создаёт впечатление пространства:

Плоскость бесконечна, но у нас есть возможность изобразить лишь её кусочек. На практике помимо параллелограмма также прорисовывают овал или даже облачко. Мне по техническим причинам удобнее изображать плоскость именно так и именно в таком положении. Реальные плоскости, которые мы рассмотрим в практических примерах, могут располагаться как угодно – мысленно возьмите чертёж в руки и покрутите его в пространстве, придав плоскости любой наклон, любой угол.
Обозначения: плоскости принято обозначать маленькими греческими буквами 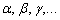 , видимо, чтобы не путать их с прямой на плоскости или с прямой в пространстве. Я привык использовать букву
, видимо, чтобы не путать их с прямой на плоскости или с прямой в пространстве. Я привык использовать букву 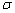 . На чертеже именно буква «сигма», а вовсе не дырочка. Хотя, дырявая плоскость, это, безусловно, весьма забавно.
. На чертеже именно буква «сигма», а вовсе не дырочка. Хотя, дырявая плоскость, это, безусловно, весьма забавно.
В ряде случаев для обозначения плоскостей удобно использовать те же греческие буквы с нижними подстрочными индексами, например, 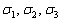 .
.
Очевидно, что плоскость однозначно определяется тремя различными точками, не лежащими на одной прямой. Поэтому достаточно популярны трёхбуквенные обозначения плоскостей – по принадлежащим им точкам, например, 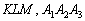 и т.д. Нередко буквы заключают в круглые скобки:
и т.д. Нередко буквы заключают в круглые скобки: 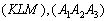 , чтобы не перепутать плоскость с другой геометрической фигурой.
, чтобы не перепутать плоскость с другой геометрической фигурой.
Не будем томиться долгими ожиданиями:
Date: 2015-04-23; view: 5404; Нарушение авторских прав