Общее уравнение плоскости

Общее уравнение плоскости имеет вид 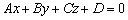, где коэффициенты 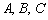одновременно не равны нулю.

Ряд теоретических выкладок и практических задач справедливы как для привычного ортонормированного базиса, так и для аффинного базиса пространства (если масло - масляное, вернитесь к уроку Линейная (не) зависимость векторов. Базис векторов). Для простоты будем полагать, что все события происходят в ортонормированном базисе и декартовой прямоугольной системе координат.

А теперь немного потренируем пространственное воображение. Ничего страшного, если у вас оно плохое, сейчас немного разовьём. Даже для игры на нервах нужны тренировки.

В самом общем случае, когда числа 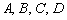не равны нулю, плоскость пересекает все три координатные оси. Например, так:

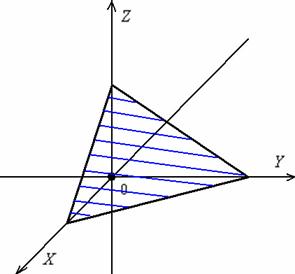
Ещё раз повторю, что плоскость бесконечно продолжается во все стороны, и у нас есть возможность изобразить только её часть.

Рассмотрим простейшие уравнения плоскостей:

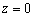
Как понимать данное уравнение? Вдумайтесь: «зет» ВСЕГДА, при любых значениях «икс» и «игрек» равно нулю. Это уравнение «родной» координатной плоскости 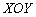. Действительно, формально уравнение можно переписать так: 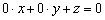, откуда хорошо видно, что нам по барабану, какие значения принимают «икс» и «игрек», важно, что «зет» равно нулю.

Аналогично:
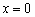– уравнение координатной плоскости ;
– уравнение координатной плоскости .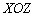

Немного усложним задачу, рассмотрим плоскость 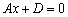(здесь и далее в параграфе предполагаем, что числовые коэффициенты не равны нулю). Перепишем уравнение в виде: 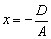. Как его понимать? «Икс» ВСЕГДА, при любых значениях «игрек» и «зет» равно некоторому числу 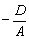. Эта плоскость параллельна координатной плоскости . Например, плоскость 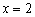параллельна плоскости и проходит через точку .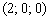

Аналогично:
– уравнение плоскости, которая параллельна координатной плоскости ;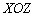
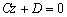– уравнение плоскости, которая параллельна координатной плоскости .

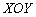Добавим членов: 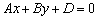. Уравнение можно переписать так: 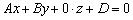, то есть «зет» может быть любым. Что это значит? «Икс» и «игрек» связаны соотношением 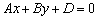, которое прочерчивает в плоскости 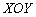некоторую прямую (узнаёте уравнение прямой на плоскости?). Поскольку «зет» может быть любым, то эта прямая «тиражируется» на любой высоте. Таким образом, уравнение 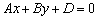определяет плоскость, параллельную координатной оси

Аналогично:
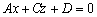– уравнение плоскости, которая параллельна координатной оси ;
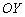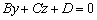– уравнение плоскости, которая параллельна координатной оси .

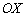Если свободные члены 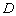нулевые, то плоскости будут непосредственно проходить через соответствующие оси. Например, классическая «прямая пропорциональность»: 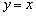. Начертите в плоскости 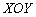прямую 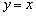и мысленно размножьте её вверх и вниз (так как «зет» любое). Вывод: плоскость, заданная уравнением 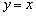, проходит через координатную ось .

Завершаем обзор: уравнение плоскости 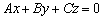проходит через начало координат. Ну, здесь совершенно очевидно, что точка 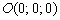удовлетворяет данному уравнению.

И, наконец, случай, который изображён на чертеже: 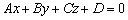– плоскость дружит со всеми координатными осями, при этом она всегда «отсекает» треугольник, который может располагаться в любом из восьми октантов.

Как грамотно построить перечисленные виды плоскостей на клетчатой бумаге – смотрите в справочных материалах о пространственных поверхностях.

Date: 2015-04-23; view: 1088; Нарушение авторских прав