Линейные неравенства в пространстве

Для понимания информации необходимо хорошо изучить линейные неравенства на плоскости, поскольку многие вещи буду похожи. Параграф будет носить краткий обзорный характер с несколькими примерами, так как материал на практике встречается довольно редко.

Если уравнение 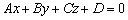задаёт плоскость, то неравенства
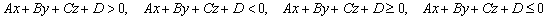задают полупространства. Если неравенство нестрогое (два последних в списке), то в решение неравенства кроме полупространства входит и сама плоскость.

Как и для линейных неравенств плоскости, справедлив аналогичный принцип: если одна точка полупространства удовлетворяет неравенству, то и ВСЕ точки данного полупространства удовлетворяют данному неравенству.

Читайте примеры и посматривайте на чертёж:

1) 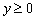. Как понимать данное неравенство? «Икс» и «зет» могут быть любыми, а вот «игрек» всегда больше либо равно нулю. Данное неравенство определяет правое полупространство; так как оно нестрогое, то координатная плоскость 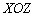входит в решение.

2) 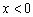– «игрек» и «зет» могут быть любыми, а вот «икс» строго меньше нуля. Неравенство задаёт дальнее от нас полупространство, и ввиду его строгости, координатная плоскость не входит в решение.

3) 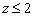Сначала мысленно начертим плоскость 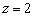– данная плоскость параллельна «родной» координатной плоскости 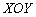и расположена на высоте 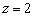(на 2 единицы выше плоскости 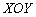). При любых «икс» и «игрек» – «зет» меньше либо равно двум. Поэтому неравенство определяет нижнее полупространство + саму плоскость .

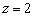4) Дана плоскость 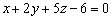. Я специально подобрал плоскость, которая «высекает» треугольник в первом октанте (такой, как на чертеже). Требуется строгим неравенством задать полупространство, которое содержит начало координат.

Составим вспомогательный многочлен и вычислим его значение в начале координат: , таким образом, искомое неравенство: .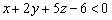

Проведённый обзор полезен не только в аналитической геометрии, но и для решения ряда задач математического анализа.

Date: 2015-04-23; view: 837; Нарушение авторских прав