
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Уравнение линии в полярных координатах
|
|
По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса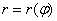 от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и непрерывно принимает значения от
от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и непрерывно принимает значения от 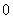 до
до 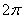 (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от
(иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от 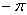 до
до 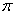 ). Каждому значению угла «фи», которое входит в область определения функции
). Каждому значению угла «фи», которое входит в область определения функции 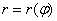 , соответствует единственное значение полярного радиуса.
, соответствует единственное значение полярного радиуса.
Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «обнаруживает» (прорисовывает) линию.
Дежурным примером полярной кривой является Архимедова спираль 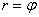 . На следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до
. На следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до 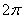 :
:
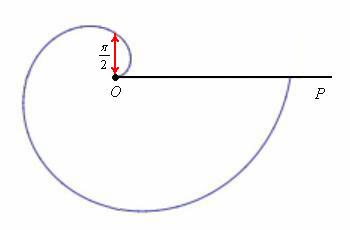
Далее, пересекая полярную ось в точке 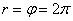 , спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая получена в диапазоне
, спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая получена в диапазоне 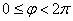 .
.
В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен 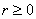 , то отрицательные углы рассматривать нельзя.
, то отрицательные углы рассматривать нельзя.
! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже
Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые очень часто встречаются в реальных практических заданиях.
Сначала простейшие уравнения и простейшие линии:
Уравнение вида 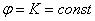 задаёт исходящий из полюса луч. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?
задаёт исходящий из полюса луч. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?
Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс
Уравнение вида 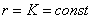 определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса
определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса 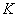 .
.
Например, 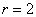 . Для наглядности найдём уравнение данной линии в прямоугольной системе координат. Используя полученную в предыдущем параграфе формулу
. Для наглядности найдём уравнение данной линии в прямоугольной системе координат. Используя полученную в предыдущем параграфе формулу 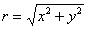 , проведём замену:
, проведём замену:
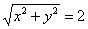
Возведём обе части в квадрат:
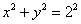 – уравнение окружности с центром в начале координат радиуса 2, что и требовалось проверить.
– уравнение окружности с центром в начале координат радиуса 2, что и требовалось проверить.
Со времён создания и релиза статьи о линейной зависимости и линейной независимости векторов я получил несколько писем от посетителей сайта, которые задавали вопрос в духе: «вот есть простая и удобная прямоугольная система координат, зачём нужен ещё какой-то косоугольный аффинный случай?». Ответ прост: математика стремится объять всё и вся! Кроме того, в той или иной ситуации немаловажно удобство – как видите, с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения 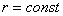 .
.
А иногда математическая модель предвосхищает научные открытия. Так, в своё время ректор Казанского университета Н.И. Лобачевский строго доказал, через произвольную точку плоскости можно провести бесконечно много прямых, параллельных данной. В результате он был ошельмован всем научным миром, но… опровергнуть данный факт никто не смог. Только спустя доброе столетие астрономы выяснили, что свет в космосе распространяется по кривым траекториям, где и начинает работать неевклидова геометрия Лобачевского, формально разработанная им задолго до этого открытия. Предполагается, что это свойство самого пространства, кривизна которого нам незаметна ввиду малых (по астрономическим меркам) расстояний.
Рассмотрим более содержательные задачи на построение:
Пример 2
Построить линию 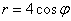
Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство 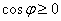 . Можно вспомнить школьные правила решения тригонометрических неравенств, но в простых случаях как этот, я советую более быстрый и наглядный метод решения:
. Можно вспомнить школьные правила решения тригонометрических неравенств, но в простых случаях как этот, я советую более быстрый и наглядный метод решения:
Представьте график косинуса. Если он ещё не успел отложиться в памяти, то найдите его на странице Графики элементарных функций. О чём нам сообщает неравенство 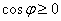 ? Оно сообщает нам о том, что график косинуса должен располагаться не ниже оси абсцисс. А это происходит на отрезке
? Оно сообщает нам о том, что график косинуса должен располагаться не ниже оси абсцисс. А это происходит на отрезке 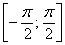 . И, соответственно, интервал
. И, соответственно, интервал 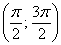 не подходит.
не подходит.
Таким образом, область определения нашей функции: 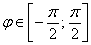 , то есть график
, то есть график 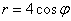 расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).
расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).
В полярных координатах часто бывает смутное представление о том, какую линию определяет то или уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла. Для бОльшей ясности к отрицательным значениям я буду «прикручивать» один оборот:
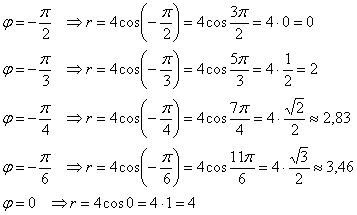
В силу чётности косинуса 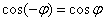 соответствующие положительные значения можно заново не считать:
соответствующие положительные значения можно заново не считать:
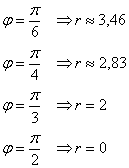
Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные засечки циркулем по рассмотренной выше технологии:
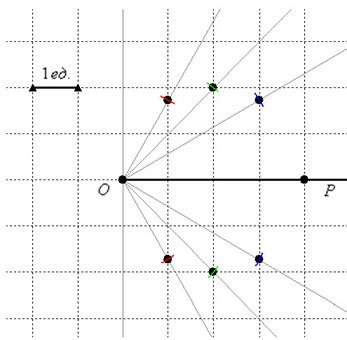
В принципе, линия отчётливо прорисовывается, но чтобы стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы 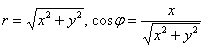 , но я расскажу вам о более хитром приёме. Обе части уравнения
, но я расскажу вам о более хитром приёме. Обе части уравнения 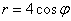 искусственно домножаем на «эр»:
искусственно домножаем на «эр»: 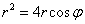 и используем более компактные формулы перехода
и используем более компактные формулы перехода 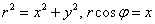 :
:
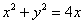
Выделяя полный квадрат, приводим уравнение линии к узнаваемому виду:
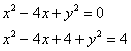
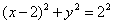 – уравнение окружности с центром в точке
– уравнение окружности с центром в точке 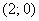 , радиуса 2.
, радиуса 2.
Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией:

Готово. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность;-)
Почему мы не рассмотрели значения угла вне промежутка 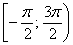 ? Ответ прост: нет смысла. Ввиду периодичности функции
? Ответ прост: нет смысла. Ввиду периодичности функции 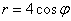 нас ждёт бесконечный бег по построенной окружности.
нас ждёт бесконечный бег по построенной окружности.
Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида 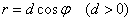 задаёт окружность диаметра
задаёт окружность диаметра 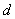 с центром в точке
с центром в точке 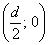 . Образно говоря, все такие окружности «сидят» на полярной оси
. Образно говоря, все такие окружности «сидят» на полярной оси 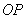 и обязательно проходят через полюс. Если же
и обязательно проходят через полюс. Если же 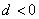 , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
, то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
Похожая задача для самостоятельного решения:
Пример 3
Построить линию 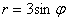 и найти её уравнение в прямоугольной системе координат.
и найти её уравнение в прямоугольной системе координат.
Систематизируем порядок решения задачи:
В первую очередь находим область определения функции, для этого удобно посмотреть на синусоиду, чтобы сразу же понять, где синус неотрицателен.
На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?
На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.
И, наконец, находим уравнение линии в декартовой системе координат.
Примерный образец решения в конце урока.
Общий алгоритм и технику построения в полярных координатах мы детализируем
и существенно ускорим во второй части лекции, но перед этим познакомимся ещё с одной распространённой линией:
Date: 2015-04-23; view: 1979; Нарушение авторских прав