
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Полярная роза
|
|
Совершенно верно, речь пойдёт о цветке с лепестками:
Пример 4
Построить линии, заданные уравнениями в полярных координатах
а) 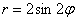
б) 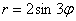
Существует два подхода к построению полярной розы. Сначала пойдём по накатанной колее, считая, что полярный радиус не может быть отрицательным:
Решение:
а) Найдём область определения функции:
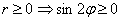
Такое тригонометрическое неравенство тоже нетрудно решить графически: из материалов статьи Геометрические преобразования графиков известно, что если аргумент функции удвоить, то её график сожмётся к оси ординат в 2 раза. Пожалуйста, найдите график функции 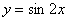 в первом же примере указанного урока. Где данная синусоида находится выше оси абсцисс? На интервалах
в первом же примере указанного урока. Где данная синусоида находится выше оси абсцисс? На интервалах 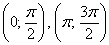 . Следовательно, неравенству
. Следовательно, неравенству 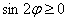 удовлетворяют соответствующие отрезки, и область определения нашей функции:
удовлетворяют соответствующие отрезки, и область определения нашей функции: 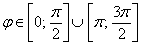 .
.
Вообще говоря, решение рассматриваемых неравенств представляет собой бесконечное множество отрезков, но, повторюсь, нас интересует только один период.
Возможно, некоторым читателям более лёгким покажется аналитический способ нахождения области определения, условно назову его «нарезка круглого пирога». Резать будем на равные части и, прежде всего, найдём границы первого куска. Рассуждаем следующим образом: синус неотрицателен, когда его аргумент находится в пределах от 0 до 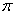 рад. включительно. В нашем примере:
рад. включительно. В нашем примере: 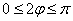 . Разделив все части двойного неравенства на 2, получаем искомый промежуток:
. Разделив все части двойного неравенства на 2, получаем искомый промежуток:
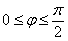
Теперь начинаем последовательно «нарезать равные куски по 90 градусов» против часовой стрелки:
– найденный отрезок 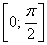 , понятно, входит в область определения;
, понятно, входит в область определения;
– следующий интервал 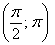 – не входит;
– не входит;
– следующий отрезок 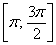 – входит;
– входит;
– и, наконец, интервал 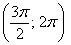 – не входит.
– не входит.
Прямо, как по ромашке – «любит, не любит, любит, не любит» =) С тем отличием, что тут не гадание. Да, прямо какая-то любовь по-китайски получается….
Итак, 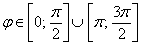 и линия
и линия 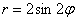 представляет собой розу с двумя одинаковыми лепестками. Чертёж вполне допустимо выполнить схематически, однако крайне желательно правильно найти и отметить вершины лепестков. Вершинам соответствуют середины отрезков области определения, которые в данном примере имеют очевидные угловые координаты
представляет собой розу с двумя одинаковыми лепестками. Чертёж вполне допустимо выполнить схематически, однако крайне желательно правильно найти и отметить вершины лепестков. Вершинам соответствуют середины отрезков области определения, которые в данном примере имеют очевидные угловые координаты 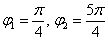 . При этом длины лепестков составляют:
. При этом длины лепестков составляют:
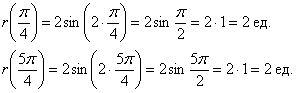
Вот закономерный результат заботливого садовника:
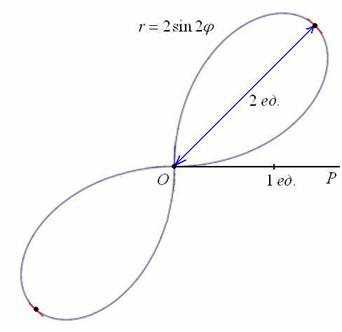
Следует отметить, что длину лепестка легко сразу усмотреть из уравнения 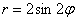 – так как синус ограничен:
– так как синус ограничен: 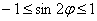 , то максимальное значение «эр» заведомо не превзойдёт двух.
, то максимальное значение «эр» заведомо не превзойдёт двух.
б) Построим линию, заданную уравнением 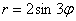 . Очевидно, что длина лепестка этой розы тоже равна двум, но, прежде всего, нас интересует область определения. Применим аналитический метод «нарезки»: синус неотрицателен, когда его аргумент находится в пределах от нуля до «пи» включительно, в данном случае:
. Очевидно, что длина лепестка этой розы тоже равна двум, но, прежде всего, нас интересует область определения. Применим аналитический метод «нарезки»: синус неотрицателен, когда его аргумент находится в пределах от нуля до «пи» включительно, в данном случае: 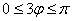 . Делим все части неравенства на 3 и получаем первый промежуток:
. Делим все части неравенства на 3 и получаем первый промежуток:
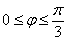
Далее начинаем «нарезку пирога кускам» по 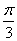 рад. (60 градусов):
рад. (60 градусов):
– отрезок 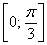 войдёт в область определения;
войдёт в область определения;
– интервал 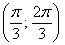 – не войдёт;
– не войдёт;
– отрезок 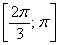 – войдёт;
– войдёт;
– интервал 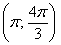 – не войдёт;
– не войдёт;
– отрезок 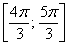 – войдёт;
– войдёт;
– интервал 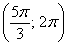 – не войдёт.
– не войдёт.
Процесс успешно завершён на отметке 360 градусов.
Таким образом, область определения: 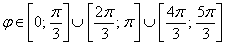 .
.
Проводимые действия полностью либо частично несложно осуществлять и мысленно.
Построение. Если в предыдущем пункте всё благополучно обошлось прямыми углами и углами в 45 градусов, то здесь придётся немного повозиться. Найдём вершины лепестков. Их длина 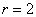 была видна с самого начала задания, осталось вычислить угловые координаты, которые равны серединам отрезков области определения:
была видна с самого начала задания, осталось вычислить угловые координаты, которые равны серединам отрезков области определения:
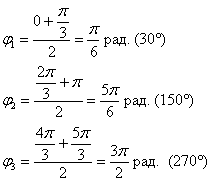
Обратите внимание, что между вершинами лепестков должны обязательно получиться равные промежутки, в данном случае 120 градусов.
Чертёж желательно разметить на 60-градусные секторы (отграничены зелёными линиями) и провести направления вершин лепестков (серые линии). Сами вершины удобно наметить с помощью циркуля – единожды отмерять расстояние в 2 единицы и нанести три засечки на прочерченных направлениях в 30, 150 и 270 градусов:
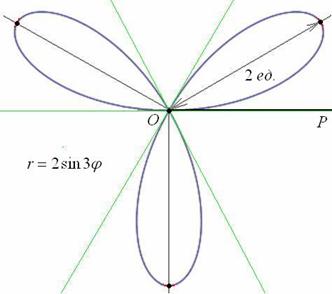
Готово. Понимаю, что занятие хлопотное, но если хотите всё оформить по уму, то придётся потратить время.
Сформулируем общую формулу: уравнение вида 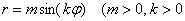 ,
,  – натуральное), задаёт полярную
– натуральное), задаёт полярную  -лепестковую розу, длина лепестка которой равна
-лепестковую розу, длина лепестка которой равна 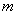 .
.
Например, уравнение 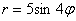 задаёт четырёхлистник длиной в 5 единиц, уравнение
задаёт четырёхлистник длиной в 5 единиц, уравнение 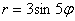 – 5-лепестковую розу с длиной лепестка в 3 ед. и т.д.
– 5-лепестковую розу с длиной лепестка в 3 ед. и т.д.
О втором подходе я хотел вообще умолчать, однако не могу пройти мимо – уж слишком он распространён. Суть состоит в том, что полярная роза часто рассматривается в обобщённых полярных координатах, где полярный радиус может быть отрицательным. Вопрос области определения отпадает, но появляются другие приколы.
Во-первых, разберёмся, как строить точки с отрицательным значением «эр». Если 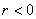 , то необходимо мысленно найти точку с таким же углом, но радиуса
, то необходимо мысленно найти точку с таким же углом, но радиуса 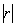 и отобразить её симметрично относительно полюса. Вернёмся к первой полярной розе
и отобразить её симметрично относительно полюса. Вернёмся к первой полярной розе 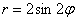 и рассмотрим интервал
и рассмотрим интервал 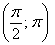 , на котором полярный радиус отрицателен. Как, например, изобразить точку
, на котором полярный радиус отрицателен. Как, например, изобразить точку 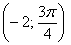 ? Мысленно находим точку
? Мысленно находим точку 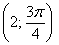 (левый верхний сектор) и отображаем её симметрично относительно полюса в точку
(левый верхний сектор) и отображаем её симметрично относительно полюса в точку 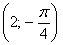 . Таким образом, когда угол принимает значения из интервала
. Таким образом, когда угол принимает значения из интервала 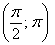 , то прорисовывается ещё один лепесток в правом нижнем секторе:
, то прорисовывается ещё один лепесток в правом нижнем секторе:
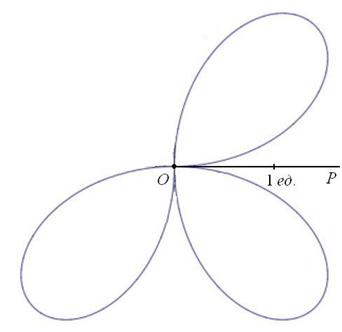
И, соответственно, когда угол проходит значения 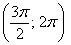 , то прорисовывается 4-ый лепесток в противоположном (левом верхнем) секторе:
, то прорисовывается 4-ый лепесток в противоположном (левом верхнем) секторе:
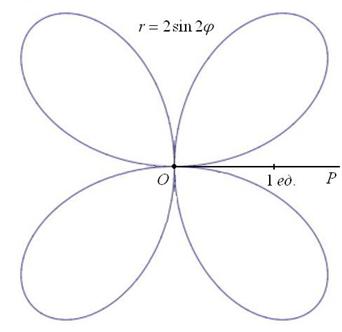
Интересно отметить, что при таком подходе вторая полярная роза 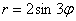 сохраняет своё количество лепестков. А происходит это по одной простой причине: когда угол проходит пустующие секторы (ещё раз посмотрите на чертёж!), то полярный радиус принимает отрицательные значения и из этих пустых секторов точки отображаются напротив, ровнёхонько накладываюсь на «легальные» лепестки.
сохраняет своё количество лепестков. А происходит это по одной простой причине: когда угол проходит пустующие секторы (ещё раз посмотрите на чертёж!), то полярный радиус принимает отрицательные значения и из этих пустых секторов точки отображаются напротив, ровнёхонько накладываюсь на «легальные» лепестки.
Сформулируем правило розы для обобщенной системы координат: уравнение вида 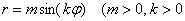 ,
,  – натуральное) задаёт полярную розу с длиной лепестка
– натуральное) задаёт полярную розу с длиной лепестка 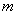 , при этом:
, при этом:
1) если - чётное, то роза имеет ровно
- чётное, то роза имеет ровно 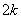 лепестков;
лепестков;
2) если - нечётное, то роза имеет ровно
- нечётное, то роза имеет ровно  лепестков.
лепестков.
Например, роза 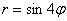 имеет 8 лепестков, роза
имеет 8 лепестков, роза 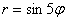 – пять лепестков, роза
– пять лепестков, роза 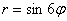 – 12 лепестков, роза
– 12 лепестков, роза 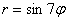 – 7 лепестков и т.д.
– 7 лепестков и т.д.
А почему закономерность столь необычна, я только что проиллюстрировал геометрически.
Какой способ выбрать, решать вам, …но я бы не особо рекомендовал использовать обобщенные полярные координаты – у преподавателя могут появиться дополнительные вопросы на счет отрицательных значений полярного радиуса (а то и вообще всё будет забраковано по этой причине)
Короткая задача для самостоятельного решения:
Пример 5
Построить линии, заданные уравнением в полярных координатах
а) 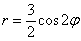
б) 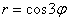
Сформулировать общее правило о количестве и длине лепестков полярной розы вида 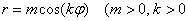 ,
,  – натуральное)
– натуральное)
В моём образце решение проведено 1-ым способом. Повторим порядок действий:
– Сначала находим область определения. При этом для лучшего понимания своих действий рекомендую соотносить аналитический способ «нарезки» с графической интерпретацией. По материалам урока Геометрические преобразования графиков выясните, как выглядят, и при необходимости начертите графики функций 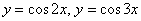 .
.
– Находим угловые координаты вершин лепестков – они расположены ровно посередине промежутков области определения.
– Выполняем чертёж. Пойдёт схематическая версия, однако желательно разметить найдённые секторы и угловые направления вершин лепестков (в случае необходимости – с помощью транспортира). Вершины удобно засекать циркулем, предварительно установив раствор, равный длине лепестка.
Существуют более солидные и общие формулы окружности, полярной розы и желающие могут с ними ознакомиться в других источниках информации. Я лишь ограничился практически значимыми (с моей точки зрения) примерами.
Предлагаю перейти ко 2-ой части занятия под названием Как построить линию в полярной системе координат?, где мы продолжим рассматривать типовые задачи, и усовершенствуем свои навыки.
Решения и ответы:
Пример 3: Решение: найдём область определения:
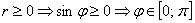
Вычислим полярные координаты точек, принадлежащих данной линии:
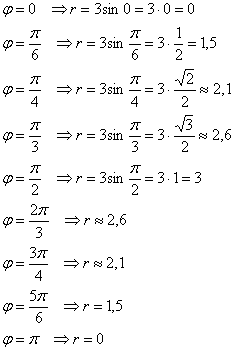
Выполним чертёж:
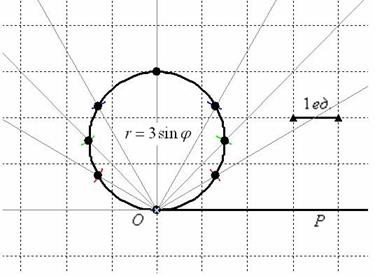
Найдём уравнение линии в декартовой системе координат:
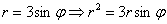
Проведём замены 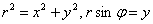 :
:
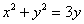
Выделим полный квадрат:
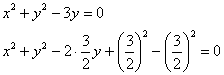
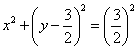 – окружность с центром в точке
– окружность с центром в точке 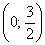 (координаты декартовы!) радиуса
(координаты декартовы!) радиуса 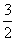 .
.
Дополнительная информация: уравнение вида 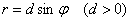 задаёт окружность диаметра
задаёт окружность диаметра 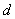 с центром в точке
с центром в точке 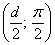 .
.
Пример 5: Решение:
а) Найдём область определения: косинус неотрицателен, когда его аргумент находится в пределах от 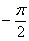 до
до 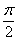 рад. включительно. В данном случае:
рад. включительно. В данном случае: 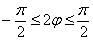 . Или:
. Или:
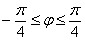 .
.
Таким образом:
– отрезок 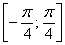 принадлежит области определения;
принадлежит области определения;
– интервал 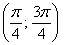 – не принадлежит;
– не принадлежит;
– отрезок 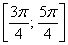 – принадлежит;
– принадлежит;
– интервал 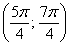 – не принадлежит.
– не принадлежит.
Область определения: 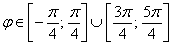 .
.
Роза имеет два лепестка, вершины которых находятся на полярной оси и её продолжении, длина лепестка равна 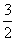 :
:
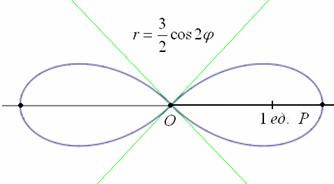
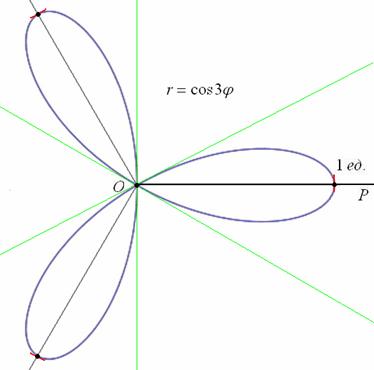
б) область определения: 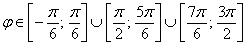 . Роза имеет три лепестка единичной длины с вершинами, имеющими следующие угловые координаты:
. Роза имеет три лепестка единичной длины с вершинами, имеющими следующие угловые координаты:
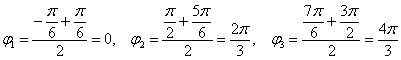
Выполним чертёж:
Уравнение вида 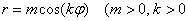 ,
,  – натуральное), задаёт полярную
– натуральное), задаёт полярную
 -лепестковую розу, длина лепестка которой равна
-лепестковую розу, длина лепестка которой равна 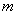 . Если рассматривается обобщенная полярная система координат, то при чётном значения «ка» количество лепестков удваивается.
. Если рассматривается обобщенная полярная система координат, то при чётном значения «ка» количество лепестков удваивается.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Date: 2015-04-23; view: 7824; Нарушение авторских прав