Взаимосвязь прямоугольной и полярной системы координат

Очевидным образом присоединим к полярной системе координат «обычную» координатную сетку и изобразим на чертеже точку :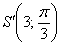

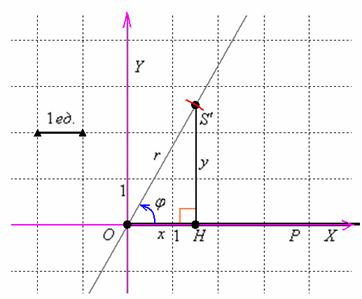
Такое присоединение всегда полезно держать в голове, когда выполняете чертёж в полярных координатах. Хотя, волей-неволей оно напрашивается и без лишнего намёка.

Установим взаимосвязь полярных 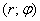и декартовых 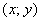координат на примере конкретной точки 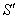. Рассмотрим прямоугольный треугольник , в котором гипотенуза равна полярному радиусу: 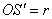, а катеты – «иксовой» и «игрековой» координатам точки 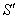в декартовой системе координат: .

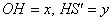Синус острого угла – есть отношение противолежащего катета к гипотенузе:

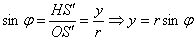
Косинус острого угла – есть отношение прилежащего катета к гипотенузе:

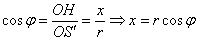
Заодно повторили определения синуса, косинуса (и чуть ранее тангенса) из программы 9-го класса общеобразовательной школы.

Пожалуйста, занесите в свой справочник рабочие формулы 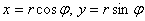, выражающие декартовы координаты точки через её полярные координаты – с ними нам придётся столкнуться ещё неоднократно, и в следующий раз прямо сейчас =)

Найдём координаты точки 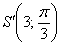в прямоугольной системе координат:

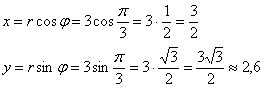
Таким образом: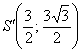

Полученные формулы открывают ещё одну лазейку в задаче построения, когда можно обойтись вообще без транспортира: сначала находим декартовы координаты точки (понятно, на черновике), затем мысленно находим нужное место на чертеже и отмечаем данную точку. На заключительном этапе проводим тонкую прямую, которая проходит через построенную точку и полюс. В результате получается, что угол якобы был отмерян транспортиром.

Забавно, что совсем отчаянные студенты, могут обойтись даже без линейки, используя вместо неё ровный край учебника, тетради или зачётной книжки – ведь о метрике позаботились производители тетрадей, 1 клетка = 5 миллиметров.

Напомнило мне всё это известный анекдот, в котором находчивые лётчики прокладывали курс по пачке Беломора =) Хотя, шутки шутками, а анекдот не так далёк от реальности, помнится, на одном из внутренних рейсов по РФ в лайнере отказали все навигационные приборы, и экипаж успешно посадил борт при помощи обычного стакана с водой, который показывал угол наклона самолёта относительно земли. А лётная полоса – вот она, из лобового стекла виднА.

Используя процитированную в начале урока теорему Пифагора, легко получить и обратные формулы: 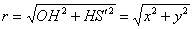, следовательно:

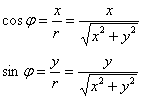
Сам угол «фи» стандартно выражается через арктангенс – абсолютно так же как и аргумент комплексного числа со всеми его заморочками.

Вторую группу формул также целесообразно поместить в свой справочный багаж.

После подробного разбора полётов с отдельно взятыми точками перейдём к закономерному продолжению темы:

Date: 2015-04-23; view: 1102; Нарушение авторских прав