Скалярное произведение в координатах, если векторы заданы суммами векторов

Пример 13

Найти скалярное произведение векторов 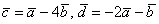, если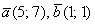

Решение: Напрашивается трафаретное решение предыдущего раздела, где мы составляли произведение и раскрывали скобки: 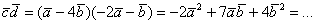. Но сейчас нам неизвестны длины векторов 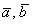и угол между ними. Зато известны координаты. Решение на самом деле будет очень простым:

Найдём вектор :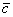

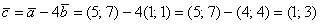
Найдём вектор :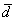

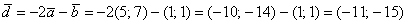
Проделаны элементарные действия с векторами, которые рассмотрены в конце урока Векторы для чайников.

Вычислим скалярное произведение:

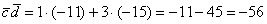
Ответ: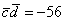

Что и говорить, иметь дело с координатами значительно приятнее.

Пример 14

Найти скалярное произведение векторов 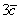и 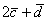, если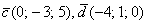

Это пример для самостоятельного решения. Здесь можно использовать ассоциативность операции, то есть не считать 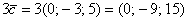, а сразу вынести тройку за пределы скалярного произведения и домножить на неё в последнюю очередь. Решение и ответ в конце урока.

В заключение параграфа провокационный пример на вычисление длины вектора:

Пример 15

Найти длины векторов 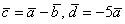, если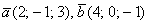

Решение: Снова напрашивается путь из предыдущего раздела: 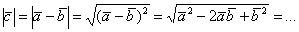, и опять мы не знаем длин векторов и угла между ними. Решение элементарно:

Найдём вектор :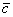

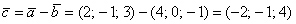
И его длину по тривиальной формуле :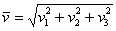

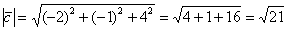
Скалярное произведение здесь вообще не при делах!

Как не при делах оно и при вычислении длины вектора :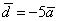
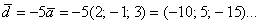Стоп. А не воспользоваться ли очевидным свойством длины вектора? Что можно сказать о длине вектора 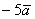? Данный вектор длиннее вектора 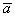в 5 раз. Направление противоположно, но это не играет роли, ведь разговор о длине. Очевидно, что длина вектора 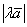равна произведению модуля числа 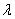на длину вектора :
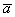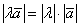– знак модуля «съедает» возможный минус числа .

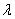Таким образом:

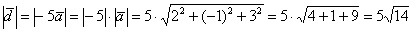
Ответ: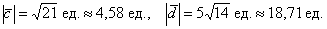

Date: 2015-04-23; view: 730; Нарушение авторских прав