Проекция вектора на координатные оси. Направляющие косинусы вектора

Рассмотрим вектор плоскости , заданный своими координатами в ортонормированном базисе 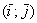. Для удобства я отложу его от начала координат:

Проекцией вектора 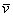на координатную ось 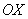является в точности его первая координата: 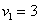(красная черта). Обозначим через 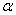угол между вектором 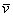и координатным вектором 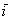: 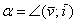(красная дуга). Тогда:
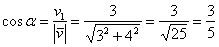(определение косинуса в прямоугольном треугольнике недавно упоминалось).

Аналогично со второй координатой: проекцией вектора 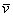на координатную ось 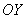является его вторая координата: 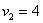(малиновая черта). Обозначим через 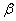угол между вектором 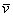и координатным вектором 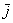: 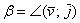(двойная малиновая дуга). Тогда:

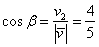
Косинусы 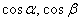называются направляющими косинусами вектора. Причём, для любого ненулевого вектора справедливо равенство 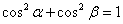. Проверим его справедливость для рассматриваемого вектора:
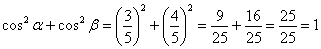, что и требовалось проверить.

Заметьте, что приведённые выше выкладки не изменятся, если вектор отложить от любой другой точки плоскости.

Итак, координаты вектора в ортонормированном базисе – это его проекции на направления соответствующих координатных векторов (координатные оси).

Направляющие косинусы ненулевого вектора 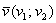, заданного в ортонормированном базисе 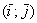, выражаются формулами 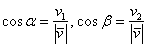, а сами координаты вектора можно выразить через его длину и данные косинусы: 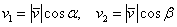, то есть: .

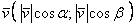Кроме того, вектор с координатами из соответствующих направляющих косинусов:

– коллинеарен исходному вектору «вэ»;

– его длина равна единице (так называемый единичный вектор).

С пространственными векторами, заданными в ортонормированном базисе 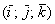, разборки точно такие же. Рассмотрим произвольный ненулевой вектор 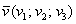. Его координаты представляют собой проекции вектора на оси 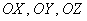соответственно. Обозначим углы данного вектора с ортами через: 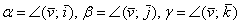. Тогда направляющие косинусы вектора выражаются формулами: 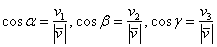, и справедливым является равенство .

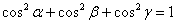В практических задачах чаще всего требуется найти направляющие косинусы вектора, заключительный пример урока:

Пример 20

Найти направляющие косинусы векторов:
а) 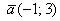, проверить, что ;
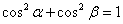б) , проверить, что .

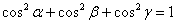Простая задача для самостоятельного решения. Фактически, она состоит в том, чтобы найти длину векторов и составить эти самые направляющие косинусы. Однако не забывайте, что вместе с направляющими косинусами нам автоматически становятся известными единичные векторы, которые коллинеарны векторам «а» и «бэ». К слову, практическая задача на нахождения единичного вектора рассмотрена в Примере №5 урока Уравнение плоскости. Ну а здесь решение и ответ совсем близко.

После изучения данного урока, у вас уже весьма приличная подготовка по аналитической геометрии. Чтобы паззл сложился окончательно, читайте статьи Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов.

Любите векторы, и векторы полюбят вас!

Решения и ответы:

Пример 2: Решение:

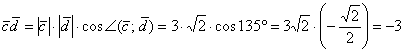
Ответ: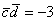

Пример 4: Решение:

Ответ: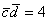

Пример 6: Решение:

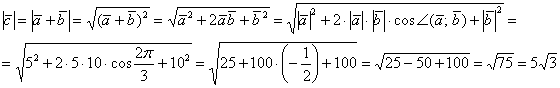
Ответ: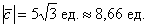

Пример 7*: Решение: Используем формулу .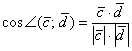
Найдём скалярное произведение:

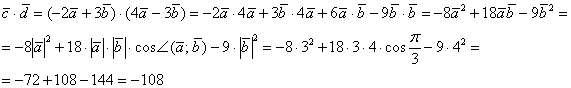
Найдём длину вектора :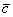

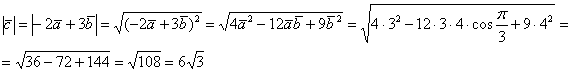
Найдём длину вектора :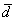

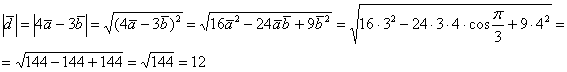
Таким образом:

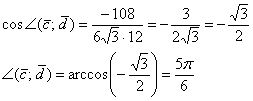
Ответ: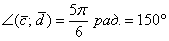

Пример 10: Решение:
а) Найдем векторы:

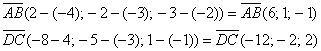
Вычислим скалярное произведение:
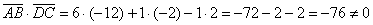, значит, прямые 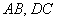не перпендикулярны.
б) Найдем векторы:

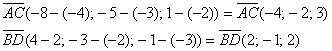
Вычислим скалярное произведение:
, значит, прямые 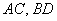перпендикулярны.
Ответ: а) прямые 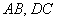не перпендикулярны, б)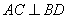

Пример 12: Решение: Составим и решим уравнение:

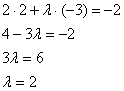
Ответ: при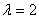

Пример 14: Решение:

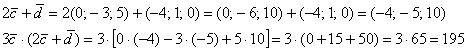
Ответ: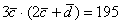

Пример 17: Решение: Найдем векторы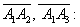

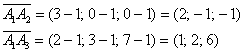
Вычислим косинус угла:

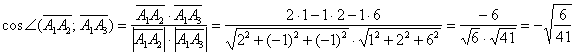
Угол: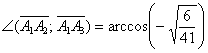
Ответ: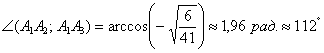

Пример 19: Решение: Найдём векторы:


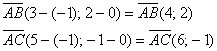
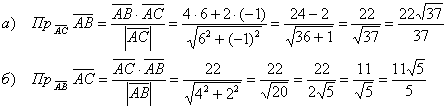
Ответ: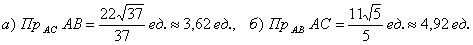

Пример 20: Решение:
а) Найдём длину вектора: .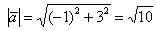
Направляющие косинусы: .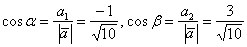
Проверка: 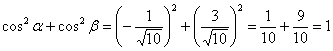, что и требовалось проверить.
б) Найдём длину вектора: .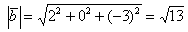
Направляющие косинусы: .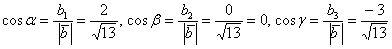
Проверка: 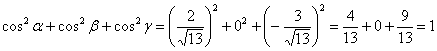, что и требовалось проверить.

Ответ: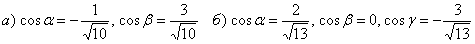

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Линейная зависимость и линейная независимость векторов.
Базис векторов. Аффинная система координат

В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой.

Линейная зависимость векторов, линейная независимость векторов, базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, абстрактный алгебраический смысл. Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства 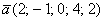. Или вектор погоды, за которым я только что сходил на Гисметео: 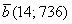– температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….

Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) носят общий алгебраический смысл (к которому можно причаститься в статье о ранге матрицы), но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания линейной алгебры. Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?

Date: 2015-04-23; view: 1833; Нарушение авторских прав