Угол между векторами и значение скалярного произведения

В Примере 1 скалярное произведение получилось положительным, а в Примере 2 – отрицательным. Выясним, от чего зависит знак скалярного произведения. Смотрим на нашу формулу: . Длины ненулевых векторов всегда положительны: 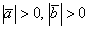, поэтому знак может зависеть только от значения косинуса.

Примечание: Для более качественного понимания нижеприведенной информации лучше изучить график косинуса в методичке Графики и свойства функции. Посмотрите, как ведёт себя косинус на отрезке .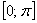

Как уже отмечалось, угол между векторами может изменяться в пределах 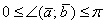, и при этом возможны следующие случаи:

1) Если угол между векторами острый: 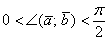(от 0 до 90 градусов), то 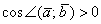, и скалярное произведение будет положительным: 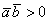. Особый случай: если векторы сонаправлены, то угол между ними считается нулевым 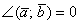, и скалярное произведение также будет положительным. Поскольку 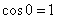, то формула упрощается: .

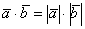2) Если угол между векторами тупой: (от 90 до 180 градусов), то 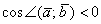, и, соответственно, скалярное произведение отрицательно: 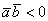. Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым: 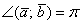(180 градусов). Скалярное произведение тоже отрицательно, так как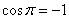

Справедливы и обратные утверждения:

1) Если 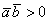, то угол между данными векторами острый. Как вариант, векторы сонаправлены.

2) Если 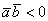, то угол между данными векторами тупой. Как вариант, векторы направлены противоположно.

Но особый интерес представляет третий случай:

3) Если угол между векторами прямой: 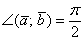(90 градусов), то 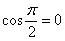и скалярное произведение равно нулю: 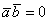. Обратное тоже верно: если 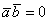, то 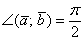. Компактно утверждение формулируется так: Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись: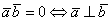

! Примечание: Рекомендую запомнить математический значок 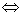, в математике его обычно читают: «тогда и только тогда», «в том и только в том случае». Как видите, стрелки направлены в обе стороны – «из этого следует это, и обратно – из того, следует это». В чём, кстати, отличие от одностороннего значка следования 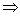? Значок 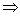утверждает, только то, что «из этого следует это», и не факт, что обратное справедливо. Например: 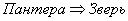, но не каждый зверь является пантерой, поэтому в данном случае нельзя использовать значок 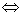. В то же время, вместо значка 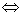можно использовать односторонний значок. Например, решая задачу, мы выяснили, что 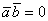и сделали вывод, что векторы ортогональны: 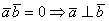– такая запись будет корректной, и даже более уместной, чем .

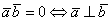Третий случай имеет большую практическую значимость, поскольку позволяет проверить, ортогональны векторы или нет. Данную задачу мы решим во втором разделе урока.

Date: 2015-04-23; view: 863; Нарушение авторских прав