Угол между векторами

Продолжаем выжимать полезные вещи из скалярного произведения. Снова посмотрим на нашу формулу 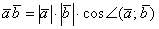. По правилу пропорции сбросим длины векторов в знаменатель левой части:

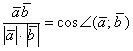
А части поменяем местами:

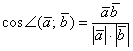
В чём смысл данной формулы? Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла между данными векторами, а, следовательно, и сам угол.

Скалярное произведение 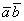– это число? Число. Длины векторов 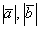– числа? Числа. Значит, дробь 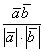тоже является некоторым числом 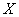. А если известен косинус угла: 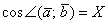, то с помощью обратной функции легко найти и сам угол: .

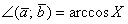Пример 7

Найти угол между векторам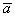и и 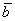, если известно, что .

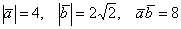Решение: Используем формулу:

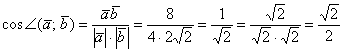
На заключительном этапе вычислений использован технический приём – устранение иррациональности в знаменателе. В целях устранения иррациональности я домножил числитель и знаменатель на .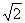

Итак, если 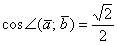, то:

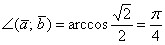
Значения обратных тригонометрических функций можно находить по тригонометрической таблице. Хотя случается это редко. В задачах аналитической геометрии значительно чаще появляется какой-нибудь неповоротливый медведь вроде , и значение угла приходится находить приближенно, используя калькулятор. Собственно, такую картину мы ещё неоднократно увидим.

Ответ: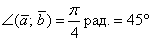

Опять, не забываем указывать размерность – радианы и градусы. Лично я, чтобы заведомо «снять все вопросы», предпочитаю указывать и то, и то (если по условию, конечно, не требуется представить ответ только в радианах или только в градусах).

Теперь вы сможете самостоятельно справиться с более сложным заданием:

Пример 7*

Даны 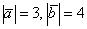– длины векторов 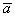, 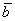и угол между ними 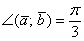. Найти угол между векторами , .

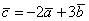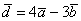Задание даже не столько сложное, сколько многоходовое.
Разберём алгоритм решения:

1) По условию требуется найти угол между векторам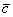и и 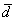, поэтому нужно использовать формулу .

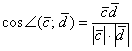2) Находим скалярное произведение 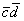(см. Примеры №№3,4).

3) Находим длину вектора 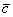и длину вектора 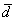(см. Примеры №№5,6).

4) Концовка решения совпадает с Примером №7 – нам известно число 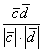, а значит, легко найти и сам угол: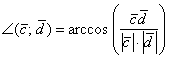

Краткое решение и ответ в конце урока.

Второй раздел урока посвящен тому же скалярному произведению. Координаты. Будет даже проще, чем в первой части.

Date: 2015-04-23; view: 734; Нарушение авторских прав