
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Скалярное произведение в координатах
|
|
Скалярное произведение векторов 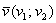 и
и 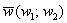 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 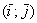 , выражается формулой
, выражается формулой 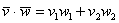
Скалярное произведение векторов 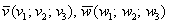 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 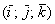 , выражается формулой
, выражается формулой 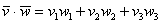
То есть, скалярное произведение равно сумме произведений соответствующих координат векторов.
Пример 8
Найти скалярное произведение векторов:
а) 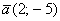 и
и 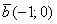
б) 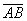 и
и 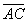 , если даны точки
, если даны точки 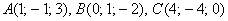
Решение:
а) Здесь даны векторы плоскости. По формуле 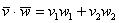 :
:
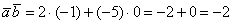
К слову: скалярное произведение получилось отрицательным, значит, угол между данными векторами является тупым. Пытливые умы могут отложить на плоскости векторы 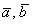 от одной точки, и убедиться, что это действительно так.
от одной точки, и убедиться, что это действительно так.
б) А тут речь идёт о точках и векторах пространства. Сначала найдём векторы:
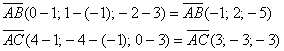
Надеюсь, эта простейшая задача у вас уже отработана.
По формуле 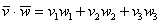 вычислим скалярное произведение:
вычислим скалярное произведение:
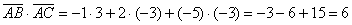
К слову: скалярное произведение положительно, значит, угол между пространственными векторами 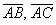 является острым.
является острым.
Ответ: 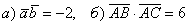
При некотором опыте скалярное произведение можно приноровиться считать устно.
Date: 2015-04-23; view: 920; Нарушение авторских прав