Лема Гауса

Добуток примітивних многочленів є примітивним многочленом.

Д-ня. Твердження досить довести для двох співмножників, а далі застосувати індукцію.

Нехай многочлени

f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ та g(x)=b_mx^m+b_m-1x^m-1+…+b₁x+b₀ – примітивні. Припустимо, що твердження леми невірне f(x)g(x)=C_n+mx^n+m+…+C₁x+C₀ не є примітивним многочленом. В такому випадку його коефіцієнти мають спільний дільник р (можна вважати, що р – просте число). Зазначимо, що всі коефіцієнти многочленів f(x) та g(x) ділитися на р не можуть, бо вони примітивні. Нехай a₀÷p, a₁÷p, … a_i-1÷p, a a_i не ділиться не p, b₀÷p, b₁÷p,… b_j-1÷p, a b_j не ділиться на p Тоді в коефіцієнті

C_i+j= a_ib_j+a_i+1b_j-1+a_i-1b_j+1+ …+ a₀b_i+j+…+ b₀a_i+j доданок а_ib_j не ділиться на p, а отже і коефіцієнт C_i+j не ділиться на p – протиріччя. Отже добуток примітивних многочленів є примітивним многочленом. ▲

Т-ма. Будь-який многочлен f(x) додатного степеня з раціональними коефіцієнтами можна подати в вигляді добутку нескоротного дробу та примітивного многочлена і це представлення єдине, т.б f(x)=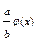

(a,b)=1 φ(x) – примітивний

Д-ня: Зведемо всі коефіцієнти многочлена f(x) до спільного знаменника та винесемо його за дужки, потім винесемо за дужки НСД коефіцієнтів того многочлена, що стоїть в дужках. Скоротимо дріб перед дужками; в дужках стоятиме примітивний многочлен.

Припустимо, що існує два представлення f(x)= 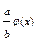* та f(x)= 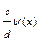(a,b)=1, (c,d)=1, де φ(x) та ψ(х) – примітивні многочлени.

Прирівняємо дві частини рівностей =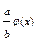

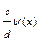
ad φ(x) = cb ψ(х)

Оскільки φ(x) та ψ(х) – примітивні многочлени, то ad÷ cb і cb÷ ad, а це означає, що cb і ad – асоційовані. Отже ad і cb відрізняються лише знаком, тому можна вважати, що ad= cb і за властивістю дробу a/b= c/d, але в такому випадку з рівності * випливає, що φ(x) = ψ(х) і представлення єдине ▲

Нехай маємо многочлен f(x) додатного степеня з Q коефіцієнтами. Позначимо m – спільний знаменник коефіцієнтів f(x) та розглянемо многочлен g(х)= m f(x) коефіцієнти якого належать Z[x]. Зрозуміло, що многочлени f(x) та g(х) мають однакові корені і є одночасно звідними та незвідними над полем Q чисел. Отже надалі можна вважати, що многочлен f(x) має цілі коефіцієнти.

Т-ма: Многочлен f(x) з цілими коефіцієнтами ненульового степеня буде звідним над Q тоді і тільки тоді, коли він звідний над Z.

Д-ня (Необхідн.) Нехай f(x) - многочлен з кільця Z[х], deg f(x)=n>0, і f(x) - звідний над полем Q. Тоді f(x) можна подати у вигляді добутку

f(x)= φ₁(x) φ₂(x) (1)

φ_і(x)є Q[х], deg φ_і(x) <n, і=1,2. Згідно з попередньою теоремою кожен многочлен з Q коефіцієнтами можна подати у вигляді добутку нескоротного дробу та примітивного многочлена, тобто φ₁= 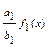φ₂= 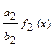де (a_i, b_i)=1, f_i - примітивні многочлени.

Підставимо значення φ₁ та φ₂ в рівність (1)

f(x)= 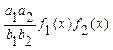(2)

позначимо дріб 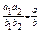(a, b)=1 та покажемо, що число a/b є цілим.

За лемою Гауса добуток 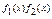- примітивний многочлен. Позначимо Ск – довільний коефіцієнт цього добутку. Тоді в силу рівності (2) кожен коефіцієнт f(x) буде мати вигляд 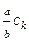. Оскільки всі коефіцієнти f(x) є цілими числами за умовою, то 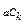÷b, а оскільки (a, b)=1 то C_k ÷ b, для довільного k. З цього випливає, що b=1. Отже a/b=aєZ і (2) перепишеться у вигляді

f(x)= а 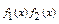, deg f_і(x) <n, тобто f(x) - звідний над Z.

(Достатність) Нехай f(x) є Z[х], звідний над полем Z, очевидно, що він буде звідним над Q.

Т-ма. (Критерій Ейзенштейна)

Якщо для многочлена

f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ додатного степеня з цілими коефіцієнтами існує таке просте число р, що є дільником всіх коефіцієнтів f(x), окрім старшого, а вільний член не ділиться не р, то f(x) - незвідний над Q

Д-ня. Припустимо, що для f(x) є Z[х] deg f(x) >0 виконуються умови теореми, але f(x) звідний над Q. За попередньою теоремою він буде звідний над Z, тоді f(x)= 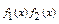f_і(x) є Z[х], deg f_і(x) < deg f(x).

Покладемо

f₁(x)=b_kx^k+b_k-1x^k-1+…+b₁x+b₀ та f₂(x)=c_lx^l+c_l-1x^l-1+…+c₁x+c₀

Перемноживши рівності та прирівнюючи коефіцієнти цього добутку до коефіцієнтів f(x) при відповідних степенях х одержимо:

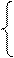a₀=b₀c₀

a₁=b₁c₀+b₀c₁

a₂=b₂c₀+b₁c₁+b₀c₂

……………………..

a_n-1= b_kc_l-1+b_k-1c_l

a_n = b_kc_l

Оскільки a₀÷ p і a не ділиться на p², то лише одне з чисел b₀ або c₀ ділиться на p. Нехай b₀ ÷p, c₀ не ділиться на p. З другої рівності враховуючи що b₀÷ p, a₁÷ p, c₀ не ділиться на p → b₁ ÷p.

З третьої рівності b₂÷p, і рухаючись далі з передостанньої одержимо, що b_k÷p. Проте в такому випадку a_n=b_kc÷ p, що суперечить умові. Отже припущення невірне і f(x) буде незвідним над Q ▲

Наслідок. Над полем Q чисел існують незвідні многочлени довільного натурального степеня.

Критерій Ейзенштейна дає лише достатню умову незвідності многочлена f(x) є Z[х] над полем Q: якщо умови критерію виконуються, то многочлен f(x)точно незвідний, якщо ні – то f(x) може бути як звідним так і незвідним над Q. У деяких випадках критерій стає застосовним при заміні х=у-у₀ (у₀=±1)

Т-ма. Якщо нескоротний дріб 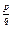є коренем многочлена f(x)

f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ n >0, то чисельник цього дробу є дільником вільного, а знаменник – старшого коефіцієнтів.

Д-ня. Нехай нескоротний дріб 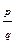- корінь f(x), тоді f(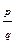)=0. Підставимо дріб у наш вираз.

a_n(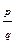)ⁿ+a_n-1(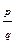)^n-1+…+a₁ 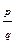+a₀=0

помножимо його на qⁿ,будемо мати

a_npⁿ+a_n-1p^n-1q+…+a₁pq^n-1+a₀qⁿ=0

Оскільки права частина рівності та сума n перших доданків лівої частини діляться на р, то a₀qⁿ ÷p, (p, q)=1 тому a₀÷p.

Аналогічно переконуємось що a_n÷q ▲

Наслідок. Якщо старший коефіцієнт многочлена f(x) дорівнює 1 (f(x) є Z[х] deg f(x) >0), то всі раціональні корені f(x) будуть дільниками вільного члена і будуть цілими числами.

Остання теорема дає необхідні умови для того, щоб раціональні числа були коренями многочлена. Зокрема, вона дає змогу вказати всі дроби, які можуть бути коренями многочлена. Щоб довести, що дріб 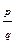є коренем f(x) необхідно буде або зробити безпосередню перевірку, або скористатися схемою Горнера. Оскільки кількість претендентів на корінь може бути досить великою, то наступна теорема дозволяє зменшити кількість обчислень.

Т-ма. Для того щоб нескоротний дріб 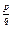був коренем многочлена f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ додатного степеня з натуральними коефіцієнтами, необхідно щоб для будь-якого натурального числа к дріб 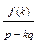єZ, i (p-kq≠0).

Д-ня. Розділимо многочлен f(x) на двочлен (x-k) з остачею. За теоремою Безу f(x)=(x-k)(b_n-1x^n-1+…+b₁x+b₀)+ +f(k). Покладемо х= 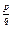, враховуючи, що f(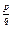)=0

0=(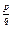 -k)(b_n-1(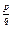)^n-1+…+b₁ 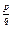+b₀)+ +f(k). Перенесемо f(x) та домножимо рівність на qⁿ

-f(x) qⁿ=(р-kq)(b_n-1p^n-1+…+b₁ pq^n-2+ +b₀q^n-1)

є Z[х], *

покажемо, що

(p-kq, q)=1. Позначимо d=СК(p-kq, q)

р= kq+(p-kq) оскільки d – дільник правої частини рівності, то d є дільником р. Оскільки (p, q)=1, то d=1. Отже (p-kq, q)=1, а це означає, що (p-kq, qⁿ)=1. Враховуючи подільність * одержимо

f(k)÷ (p-kq), 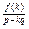єZ. ▲

Наслідок. Якщо старший коефіцієнт многочлена f(x) є Z[х] додатного степеня дорівнює 1, і α – корінь f(x), то для довільного к є Z дріб 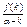є цілим числом, за умови, що α-к≠0.

Як правило, останню теорему та її наслідок використовують при к=±1 і тоді теорема звучить так: для того, щоб нескоротний дріб 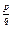був коренем f(x) необхідно щоб дроби та 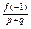одночасно були цілими числами.

14. Многочлени над полем дійсних чисел.

Лема 1. Будь-який многочлен непарного степеня з дійсними коефіцієнтами має принаймні 1 дійсний корінь.

Д-ня. Нехай deg f(x)=n=2k+1 – непарне число, і f(x)=a_nxⁿ+…+a₁x+a₀, an>0. Як відомо многочени є неперервними функціями і їх поведінка на нескінченостях визначається поведінкою старшого члена тобто

f(x) = a_nxⁿ=+∞, крім того

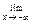f(x)= 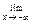a_nxⁿ= -∞

Отже існують такі числа a,b єR, що f(a)<0, a f(b)>0. За теоремою Больцано-Коші існує число c, cє[a, b], таке що f(c)=0, c єR. Отже c – корінь f(x) ▲

Лема 2. Будь-який многочлен f(x) ненульового степеня з дійсними коефіцієнтами має принаймні 1 комплексний корінь.

Д-ня. Нехай deg f(x)=n, тоді n=2^k*q, де k≥0, (q, 2)=1.

Доведемо твердження леми індукцією по к.

1. Нехай к=0, тоді n=q – непарне число, і за лемою1 f(x) має дійсний (комплексний) корінь.

2. Припустимо, що твердження вірне для всіх натуральних чисел менших за к, тобто для многочленів степінь яких ділиться на 2^к-1 і не ділиться на 2^к .

3. Доведемо, що твердження вірне для многочленів степінь яких ділиться на 2^к.

Нехай f(x) такий многочлен тобто

deg f(x) =2^kq=n. У полі розкладу Δ f(x) має корені α₁, α₂,…, α_n. Сконструюємо елемент β_ij виду: α_iα_j+C(α_i+α_j) де C - довільне число єR, i<j. таких елементів буде

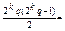2^k-1q(2^kq-1)=2^k-1q₁,

де q₁=q(2^kq-1)-непарне число.

Розглянемо многочлен

φ(х)= 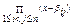, степеня 2^k-1q₁ коренями якого є β_ij і тільки вони. Зауважимо, що при перестановках α_k ↔ α_m і навпаки многочлени β_ij не змінюються і тому φ(х) є симетричним відносно α₁, α₂,…, α_n.

Враховуючи, що α₁, α₂,…, α_n корені многочлена з дійсними коефіцієнтами та застосовуючи теорему, яка є наслідком з формули Вієта одержимо, φ(х) також матиме дійсні коефіцієнти. За припущенням індукції (оскільки deg f(x) =2^k-1q₁) многочлен φ(х) з дійсними коефіцієнтами матиме принаймні 1 комплексний корінь β_ijєС Таким чином, для будь-якого дійсного числа С можна вказати пару індексів i та j, (1≤i<j≤n) при яких β_ij=α_iα_j+C(α_i+α_j) є комплексним числом. Зрозуміло також, що різним дійсним числам С₁ і С₂ відповідають різні пари індексів. Проте, оскільки множина дійсних чисел нескінченна, а множина пар (i, j) (таких що1≤i<j≤n) скінченна, то можна вибрати пару чисел С₁ і С₂ (С₁ ≠ С₂), яким відповідатиме одна і та ж пара індексів, тобто

β_ij =α_iα_j+C₁(α_i+α_j)

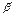_ij = α_iα_j+C2(α_i+α_j)

β_{ij 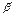ij} – комплексні числа.

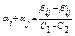
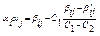
Очевидно, що α_i та α_j є коренями квадратного рівняння з комплексними коефіцієнтами

Z² - (α_i + α_j) Z + α_iα_j=0

Отже α_і та αj є комплексними коренями многочлена f(х) ▲.

Date: 2015-04-23; view: 1100; Нарушение авторских прав