Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать неотразимый комплимент
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Наслідки з теореми
|
|
1. Многочлен додатного степеня з числовими коефіцієнтами має над полем комплексних чисел стільки коренів, якого є його степінь
Д-ня. Нехай f(x) – многочлен з числовими коефіцієнтами і deg f(х)>0. За основною теоремою алгебри f(x) має комплексний корінь αi, тоді
f(x)(х-α1)↔ f(x)=(х-α1)g(х). Якщо degg(х)=0, то g(х)=an, тобто f(x)=an(х-α1) і в полі комплексних чисел f(x) має рівно один корінь.
Нехай degg(х)>0, тоді, за основною теоремою існує α2 (комплексне число), яке є коренем g(х), тобто
g(х)=(х-α2)*g1(х), тоді
f(x)=(х-α1)*(х-α2)*g1(х). Продовжуючи цей процес далі, та розкладаючи многочлени gi(х) одержимо:
f(x)=an(х-α1)*(х-α2)*…*(х-αn), тобто числа α1, α2,…αn є коренями многочлена f(x). Цих коренів більше ніж n за доведеним раніше бути не може. ▲
2. Поле комплексних чисел є полем розкладу будь-якого многочлена додатного степеня з числовими коефіцієнтами (Випливає з попереднього наслідку)
3. Поле комплексних чисел є алгебраїчно замкненим, тобто є полем розкладу будь-якого многочлена з комплексними коефіцієнтами.
4. Над полем комплексних чисел незвідними є лише многочлени першого степеня і тільки вони.
5. Над полем комплексних чисел умова існування кратних множників многочлена еквівалентна умові існування кратних коренів.
6.Над полем комплексних чисел многочлени f(х) та g(х) мають спільні множники тоді і тільки тоді, коли вони мають спільні корені.
7. Якщо многочлен f(х) з дійсними коефіцієнтами має комплексний корінь α=a+bi, то його коренем буде і число спряжене до α, 
= a - bi.
Д-ня. Нехай многочлен
f(x)=anxn+an-1xn-1+…+a1x+a0 є R має комплексний корінь α. Тобто f(α)=anαn+an-1αn-1+…+a1α+a0=0.
Візьмемо комплексне спряжене від многочленів останньої рівності
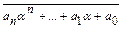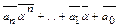=0 →
=0
аі – дійсні числа, вони співпадають з своїми спряженими: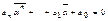 
f( )=0, тобто - корінь f(х) ▲
8. Якщо многочлен f(х) з дійсними коефіцієнтами має комплексний корінь α кратності к, то він має корінь тієї ж кратності.
9. Над полем дійсних чисел незвідними можуть бути многочлени першого або другого степеня і тільки вони.
Д-ня. Нехай f(х) є незвідним многочленом над дійсним полем. Припустимо, що deg f(х)>2. За лемою наслідком 7 він матиме комплексний корінь α і , тоді f(x)=(x-α)(x- )*g(x) причому
deg g(x) ≥1
f(x)=(x2 – αx - x + α )*g(x), або
f(x)=(x2 - (α + )x+ α )*g(x), де
(α + ) є R, α є R таким чином многочлен в дужках має дійсні коефіцієнти і враховуючи що deg g(x)≥1 робимо висновок, що f(x) буде незвідним над R ▲
Date: 2015-04-23; view: 377; Нарушение авторских прав