Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Канонические уравнения кривых и поверхностей второго порядка

⇐ ПредыдущаяСтр 37 из 157Следующая ⇒

Аналитическая геометрия и линейная алгебра

 

 

Отчетность: контрольная работа, экзамен

 

 

Часть I. Аналитическая геометрия

 

Системы уравнений. Матрицы и определители

1. Определители 2го и 3го порядка. Решение систем линейных уравнений малых порядков. Формулы Крамера. Операции над матрицами. Обратная матрица, существование и вычисление.

 

Векторная алгебра

2. Понятие вектора. Линейные операции над векторами. Линейная зависимость векторов.

3. Базис на плоскости и в пространстве. Разложение вектора по базису. Системы координат на плоскости и в пространстве. Преобразован6ие декартовой системы координат на плоскости и в пространстве.

4. Скалярное произведение векторов. Векторное, смешанное и двойное векторное произведение. Вычисление этих произведений в прямоугольных декартовых координатах.

 

Линейные образы: прямая на плоскости, прямая и плоскость в пространстве

5. Различные типы уравнений прямой на плоскости. Задачи на прямую на плоскости.

6. Различные типы уравнений плоскости.

7. Прямая и плоскость в пространстве, угол между прямыми и плоскостями. Задачи на взаимное положение прямой и плоскости.

 

Канонические уравнения кривых и поверхностей второго порядка

8. Линии второго порядка. Определение линий второго порядка, как геометрического места точек. Канонические уравнения эллипса, гиперболы, параболы.

9. Исследование линий второго порядка.

10. Канонические уравнения поверхностей второго порядка.

 

 

Рекомендуемая литература

Ильин В.А., Позняк Э.Г., Аналитическая геометрия, М., Наука, 1988.

Беклемишев Д.В., Курс аналитической геометрии и линейной алгебры, М, Наука, 1984.

Канатников А.Н., Крищенко А.П., Аналитическая геометрия, М., Изд. МГТУ им. Н.Э. Баумана, 1999.

Бахвалов С.В., Моденов П.С., Пархоменко А.С., Сборник задач по аналитической геометрии, М., Наука, 1976.

Клетеник Д.В., Сборник задач по аналитической геометрии, М., Наука, 1975.

Ефимов А.В., Каракулин А.Ф. и др., Сборник задач по математике для втузов, ч.1, М., Физматлит, 2001.

 

Задание по разделу «Аналитическая геометрия»

 

  1. Вычислить определитель матрицы

 

Вариант 1 Вариант 2 Вариант 3

 

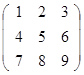
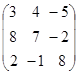
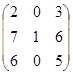
Вариант 4 Вариант 5 Вариант 6

 

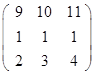
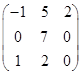
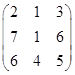
  1. Решить систему уравнений

 

Вариант 1 Вариант 2 Вариант 3
x1 + 2x2 + 3x3 + 4x4 = 5 x1 + x2 - x3 + x4 = 4 2x1 + 3x2 + 11x3 + 5x4 = 2
2x1 + x2 + 2x3 + 3x4 = 1 2x1 - x2 + 3x3 - 2x4 = 1 x1 + x2 + 5x3 + 2x4 = 1
3x1 + 2x2 + x3 + 2x4 = 1 x1 - x3 + 2x4 = 6 2x1 + x2 + 3x3 + 2x4 = - 3
4x1 + 3x2 + 2x3 + x4 = - 5 3x1 - x2 + x3 - x4 = 0 x1 + x2 + 3x3 + 4x4 = - 3
Вариант 4 Вариант 5 Вариант 6
x1 + 2x2 + x3 = 8 x1 + x2 - x3 + x4 = 4 2x1 - 3x2 + x3 + 2x4 = -7
x2 + 3x3 + x4 = 15 4x1 + 3 x2 - x3 + 2x4 = 6 x1 + 4x2 + 2x3 + x4 = -1
4x1 + x3 + x4 = 11 8x1 + 5x2 - 3x3 + 4x4 = 12 x1 - 4x2 + 2x4 = - 5
x1 + x2 + 5x4 = 23 3x1 + 3x2 - 2x3 + 2x4 = 6 2x1 - 3 x2 - 3x3 + 4x4 = 1

 

  1. Найти обратную матрицу методом элементарных преобразований
Вариант 1 Вариант 2 Вариант 3

 

 

 

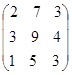
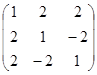
Вариант 4 Вариант 5 Вариант 6

 

 

 

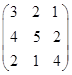
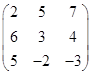
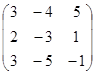
  1. Даны три вектора p = {3; -2; 1}, q = {-1; 1; -2}, r = {2; 1; -3}

Найти разложение вектора c по базису p, q, r.

 

Вариант 1 Вариант 2 Вариант 3

c = {11; -6; 5} c = {9; -6; 4} c = {7; 3; 6}

 

 

  Вариант 4 Вариант 5 Вариант 6
  c = {3; -4; -3} c = {1; 5; -6} c = {-7; -7; 5}
 
     

 

  
         
  1. Даны три некомпланарных вектора a, b, c

Вычислить, при каких значениях λ и μ векторы

 

λa + b + c, a +λb + c, a + b +λcкомпланарны   Вариант 1
λa +μb + c, a +λb +μcколлинеарны   Вариант 2
a + b, b + c, a -λcкомпланарны   Вариант 3
λa + b,λb + c, a +λcкомпланарны Вариант 4
2(а +μb) -λcи2a +4 b + cравны Вариант 5
λa +μb + c,λa +λb + cнеколлинеарны Вариант 6

 

 

  1. Составить каноническое уравнение прямой

 

Вариант 1 Вариант 2 Вариант 3

 

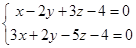
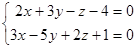
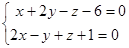
Вариант 4 Вариант 5 Вариант 6

 


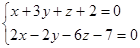
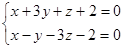
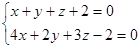
7. Составить уравнение плоскости, проходящей через заданную прямую

 

Вариант 1 Вариант 2 Вариант 3
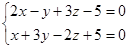
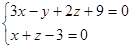
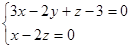
  параллельно векторуl{2,-1,-2}   и точку М{4,-2,-3} Перпендикулярно плоскости x – 2y + z + 5 = 0
    Вариант 4     Вариант 5     Вариант 6
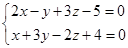
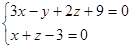
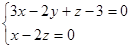
  и точку М{4,-2,-3}   параллельно векторуl{2,-1,-2}   и точку М{1, 1, 0}

 

  1. Даны координаты вершин тетраэдра A; B; C; D

Найти

1) Объем тетраэдра;

2) Площадь грани ABC;

3) Уравнение прямой AD

 

Вариант Координаты A B C D
  (4, 2, 5) (0, 7, 2) (0, 2, 7) (1, 5, 0)
  (4, 1, -2) (2, 0, 0) (-2, 3,-5) (1, 4, 2)
  (4, 1, -2) (2, 0, 0) (-2, 3,-5) (1, 0, -1)
  (4, 2, 5) (0, 7, 2) (0, 2, 7) (1, 1, 0)
  (4, 3, 5) (0, 7, 2) (0, 2, 7) (1, 1, 1)
  (4, 0, 5) (0, 7, 2) (0, 2, 7) (1, 1, 0)

 

     

 

  1. При каких значениях m и n уравнение определяет:
  1. Центральную линию;
  2. Линию без центра;
  3. Линию, имеющую бесконечно много центров.

 

 

Вариант 1 5x2 + 14xy + my2 + 20x + ny – 18 = 0
Вариант 2 2x2 - 4xy + my2 + 8x - ny + 9 = 0
Вариант 3 x2 + 6xy + my2 + 3x + ny – 4 = 0
Вариант 4 5x2 + 4xy + my2 + 8x + ny +5 = 0
Вариант 5 mx2 + 12xy + 9y2 + 4x + ny – 13 = 0
Вариант 6 6xy + my2 - 12x + ny + 11 = 0

 

  1. Привести уравнение к каноническому виду, определить тип уравнения, определить геометрический образ, определяемый уравнением, найти каноническую систему координат и построить линию второго порядка.

 

 

Вариант 1 4xy + 3y2 + 16x + 12y – 36 = 0
Вариант 2 3x2 + 10xy + 3y2 – 2x – 14y – 13 = 0
Вариант 3 25x2 – 14xy + 25y2 + 64x – 64y – 224 = 0
Вариант 4 5x2 + 12xy + 10y2 - 6x + 4y – 1 = 0
Вариант 5 2x2 - 4xy + 5y2 + 8x - 2y + 9 = 0
Вариант 6 5x2 + 2xy + 5y2 - 12x + 20y + 32 = 0

 

 

Часть II. Линейная алгебра

 


⇐ Предыдущая32333435363738394041Следующая ⇒





Date: 2015-04-23; view: 1553; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.013 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию