Теорема Ейлера і Ферма

Т-ма. Нехай a і b цілі числа, mєN тоді еквівалентні між собою 3 умови:

1. a і b дають однакові остачі при діленні на m: a=mq₁+r, b=mq₂+r, 0≤ r ≤m

2. (a-b)÷mєZ

3. Числа a і b відрізняються на ціле число, що є кратним m: a=b+mq, qєZ

Д-ня Доведемо еквівалентність умов за схемою 1→2→3→1

1) покажемо, що з 1→2. За умовою a=mq₁+r, b=mq₂+r, віднімемо рівності: a-b=m(q₁-q₂). Оскільки m(q₁-q₂)÷m то (a-b)÷m, тобто виконується 2

2) покажемо, що2→3. Нехай

(a-b)÷m, за означенням подільності націло a-b=mq, qєZ, звідки a=b+mq, тобто виконується умова 3.

3) 3→1. Нехай виконується a=b+mq, qєZ, або це можна переписати a-b=mq Розділимо a і b на m з остачею:

_ a=mq₁+r₁ 0≤ r₁ r₂ <m

b=mq₂+r₂

віднімемо почленно останні рівності

a-b = m(q₁-q₂)+(r₁-r₂) враховуючи рівність a-b=mq приходимо до висновку, що q₁-q₂ =0, r₁-r₂ =0 і числа a і b дають однакові остачі при діленні на m. ▲

Таким чином, вказана теорема з різних сторін характеризує одну й ту ж саму властивість подільності чисел a і b на число m.

Означ. Нехай a і b єZ, mєN. Числа a і b називають конгруентними по модулю m, якщо виконується хоча б одна із умов 1-3 вказаної теореми. Позначення: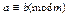

З означення маємо, що

1.a=mq₁+r або b =mq₂+r,

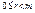
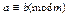
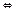2. (a-b)÷mєZ

3.a=b+mq, qєZ

Наприклад,

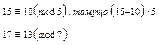
Date: 2015-04-23; view: 665; Нарушение авторских прав