
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Властивості
|
|
1. Якщо p – просте число, то 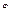 (p)=p-1. Доведення випливає з означення функції Ейлера.
(p)=p-1. Доведення випливає з означення функції Ейлера.
2. Якщо p – просте число, то 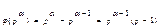
Д-ня. Випишемо всі натуральні числа від 1 до pα та розіб’ємо їх на групи по p чисел {1,2,3,…p}, {p+1,p+2,…2p} …{pα+p+1,…pα}. Очевидно, що всіх груп буде pα-1 (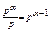 )
)
Очевидно, що в кожній групі всі числа, крім одного (останнього) взаємно прості з pα. Отже всіх чисел взаємно простих з pα буде (p-1)pα-1 тобто 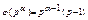 ▲
▲
3. Функція Ейлера мультиплікативна.
Д-ня. Для доведеня цього факту достатньо показати, що для довільних m,nє N і (m,n)=1 φ(mn)=φ(m)φ(n). Випишемо всі числа, які не перевищують mn та з’ясуємо, які з них взаємно прості з mn. Зрозуміло, що число взаємно просте з mn тоді і тільки тоді, коли воно взаємно просте з m і з n. Розташуємо числа від 1 до mn у таблицю, з’ясуємо скільки чисел взаємно простих з m міститься у таблиці
1 2 … r … m
m+1, m+2 … m+r … 2m
2m+1, 2m+2 … 2m+r … 3m
………………………………………….
(n-1)m+1, (n-1)m+2 … (n-1)m+r …mn
Для цього покажемо, що в кожному стовпчику всі числа або одночасно взаємно прості з m або не взаємно прості. Виберемо довільний r-тий стовпчик, всі числа цього стовпчика мають вигляд: km+r, 0≤k≤n-1. За властивістю НСД двох чисел (a=bq+r (a,b)=(b,r)) маємо (km+r,m)=(m,r). Отже НСД всіх чисел стовпчика з числом m той же самий, що і з числом r і визначається номером стовпчика (числом r). Таким чином кількість стовпчиків у яких всі числа взаємно прості з m буде стільки ж скільки взаємно простих чисел міститься у першому рядку, а їх буде φ(m). Покажемо, що всі числа у довільно вибраному стовпці при діленні на n дають різні остачі. Нехай це не так і якийсь стовпець має 2 числа, що дають однакові остачі при діленні на n. _ k1m+r=nq1+s
k2m+r=nq2+s
m(k1-k2)=n(q1-q2)
(0≤k1,k2…≤n-1, k1≠k2, 0≤ s ≤0)
Оскільки права частина ділиться на n і (m,n)=1 то (k1-k2)÷n. Проте |k1-k2|<n звідки k1-k2=0 і k1=k2, що суперечить припущенню. Отже всі числа в стовпці дають попарно різні остачі при при діленні на n: 0, 1, 2,… n-1. Отже серед чисел стовпця взаємно простих з n буде стільки ж, скільки є взаємно простих чисел від 1 до n, а їх φ(n). Таким чином у таблиці міститься φ(m) взаємно простих з m стовпчиків і в кожному стовпчику φ(n) чисел, які взаємно прості з n, отже всіх взаємно простих з mn чисел буде φ(m)φ(n). Звідки φ(mn)=φ(m)φ(n).▲
4. Якщо n=pα11pα22…pαkk то
φ(n)=n(1-  )(1-
)(1- 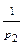 )…(1-
)…(1- 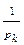 )
)
Д-ня. В силу мультиплікативності функції φ, φ(n)=φ(pα11pα22…pαkk) = φ(pα11)φ(pα22)…φ(pαkk) за властивістю 2
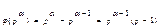
φ(n)= pα11 (1-  ) pα22 (1-
) pα22 (1-  )… pαkk (1-
)… pαkk (1- 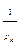 )=n(1-
)=n(1-  )(1-
)(1-  )…(1-
)…(1- 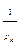 )
)
▲
5. Формула Гауса 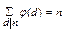
Д-ня. 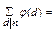 (1+ φ(p1)+φ(p12)+…
(1+ φ(p1)+φ(p12)+…
+φ(p1α1))(1+φ(p2)+…+φ(p2α2))…(1+ +φ(pk)+…+φ(pkαk))=(1+p1-1+p12-p1+… +p1α1-p1α1-1)(1-p2-1+…+p2α2-p2α2-1)… (1+pk-1+…+pkαk-pαk-1)=p1α1p2α2…pkαk=n
▲
6. При n > 2 φ(n) є числом парним.
10. Конгруенції 1-го степеня з одним невідомим у кільці цілих чисел.
Конгруенцією з одним невідомим за модулем m називається конгруенція виду
f(x)=anxn+an-1xn-1+…+a1x+ a0≡0(mod m)
числа ai є Z, i=0…n.
Якщо an не ділиться націло на m, то степінь n називається степенем конгруенції. Якщо an ділиться націло на m то конгруенція має степінь < n.
Розв’язком конгруенції з одним невідомим називається ціле число α при підстановці якого у дану конгруенцію одержимо вірну числову конгруенцію f(α)≡0(mod m)
Зрозуміло, що разом з α дану конгруенцію задовольняє будь-яке число β=α+mt, що належить тому ж класу лишків, що і α, тобто розв’язком даної конгруенції є цілий клас лишків 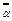 . Знайти розв’язки даної конгруенції можна наприклад перебрати повну систему лишків по модулю n. Враховуючи, що в ній міститься m представників кожного класу, дана конгруенція матиме не більше ніж m розв’язків.
. Знайти розв’язки даної конгруенції можна наприклад перебрати повну систему лишків по модулю n. Враховуючи, що в ній міститься m представників кожного класу, дана конгруенція матиме не більше ніж m розв’язків.
Дві конгруенції називаються рівносильними, якщо вони мають по модулю m одну й ту ж саму множину розв’язків. До операцій, які дозволяють перейти від даної конгруенції до рівносильної їй відносять: додавання до обох частин конгруенції многочлена з цілими коефіцієнтами, кратними модулю; множення (ділення) обох частин конгруенції на число взаємно просте з модулем; множення (ділення) обох частин конгруенції і модуля на натуральне число.
Означ. Лінійною конгруенцією з одним невідомим називають конгруенцію виду ax≡b(mod m), (1) a,b єZ
Дослідження лінійної конгруенції.
1. Якщо (a,m)=1, то конгруенція має єдиний розв’язок, який можна знайти за формулою x≡baφ(m)-1(mod m) (2)
Помножимо конгруенцію (1) на aφ(m)-1
Це можна зробити, бо (aφ(m)-1, m)=1
a aφ(m)-1x≡b aφ(m)-1 (mod m),
a aφ(m)x≡b aφ(m)-1 (mod m). Оскільки (a,m)=1, то за теоремою Ейлера будемо мати: 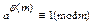 , тому в останній конгруенції будемо мати: x≡baφ(m)-1(mod m). Покажемо, що конгруенції (1) та (2) рівносильні. Нехай β-розв’язок конгруенції (2), тобто β≡bаφ(m)(mod m). Помножимо обидві частини останньої конгруенції на а одержимо: аβ≡bаφ(m)(mod m), за теоремою Ейлера маємо
, тому в останній конгруенції будемо мати: x≡baφ(m)-1(mod m). Покажемо, що конгруенції (1) та (2) рівносильні. Нехай β-розв’язок конгруенції (2), тобто β≡bаφ(m)(mod m). Помножимо обидві частини останньої конгруенції на а одержимо: аβ≡bаφ(m)(mod m), за теоремою Ейлера маємо
аβ≡b(mod m), отже β – розв’язок конгруенції (1). Нехай α – розв’язок конгруенції (1), тобто aα≡b(mod m) помноживши обидві частини на aφ(m)-1
одержимо α≡bаφ(m)-1(mod m) тобто α-є розв’язком конгруенції (2), а раз так то (1) і (2) рівносильні.
2. Нехай (a, m)=d≠1 i b не ділиться націло на d, то конгруенція розв’язку не має. Справді, перепишемо (1) у вигляді ax=b+mt, тоді оскільки ax÷d і b÷d, то mt÷d що є протиріччям.
3. Нехай (a, m)=d і b ÷ d, тоді конгруенція (1) має d розв’язків.
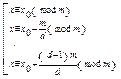 (3)
(3)
\де х0 – розв’язок конгруенції 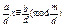 (4)
(4)
Покажемо, що конгруенції (1) і (4) рівносильні. Нехай α – один з розв’язків конгруенції (1) тобто aα≡b(mod m). Поділимо обидві частини конгруенції і модуль на число d отримаємо 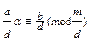 , отже α – розв’язок (4).
, отже α – розв’язок (4).
Нехай тепер α – розв’язок конгруенції (4), тобто 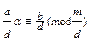 , помножимо обидві частини конгруенції та модуль на α:
, помножимо обидві частини конгруенції та модуль на α:  тобто α – розв’язок (1) і рівності (1) (4) рівносильні.
тобто α – розв’язок (1) і рівності (1) (4) рівносильні.
Розглянемо конгруенцію (4) оскільки у ній (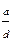 ,
, 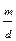 )=1, то (4) має один розв’язок, наприклад x0+(m/d)t
)=1, то (4) має один розв’язок, наприклад x0+(m/d)t
Розглянемо числа x0; x0+ 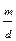 ; x0+
; x0+ 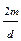 ; … x0+
; … x0+ 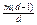 , (5) де х0 – найменший невід’ємний лишок по модулю
, (5) де х0 – найменший невід’ємний лишок по модулю 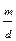 . Очевидно, що числа (5) є розв’язками конгруенції (4), а раз так, то і рівносильної їй конгруенції (1). Покажемо, що числа (5) належать різним класам лишків по модулю m, припустимо що це не так і
. Очевидно, що числа (5) є розв’язками конгруенції (4), а раз так, то і рівносильної їй конгруенції (1). Покажемо, що числа (5) належать різним класам лишків по модулю m, припустимо що це не так і
x0+ 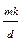 ≡ x0+
≡ x0+ 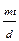 (mod m), k,tє[0,d-1]
(mod m), k,tє[0,d-1]
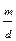 (k-t)≡ 0 (mod m). Покажемо, що
(k-t)≡ 0 (mod m). Покажемо, що 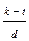 є Z. Оскільки k,t≤d-1, то |k-t|≤d-1, (k-t)÷d ↔ k-t=0, k=t, отже вказані числа належать одному класу лишків по модулю m.
є Z. Оскільки k,t≤d-1, то |k-t|≤d-1, (k-t)÷d ↔ k-t=0, k=t, отже вказані числа належать одному класу лишків по модулю m.
11. Многочлени над числовим полем. Найбільший спільний дільник двох многочленів. Алгоритм Евкліда.
Нехай К – довільна область цілісності
Многочленом або поліномом від 1 змінної над областю цілісності К називається вираз виду:
f(x)=anxn+an-1xn-1+…+a1x+a0 (1)
де ai K (i=0…n), n N 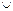 {0}.
{0}.
При цьому ai називають коефіцієнтами многочлена, aixi – ітим членом многочлена, зокрема anxn назив старшим членом, a0 – вільним членом многочлена, xi – ітим степенем елемента x.
Якщо an≠0, то n назив. степенем многочлена і позначають deg f(x)
Многочленами нульового степеня є константи з кільця К, т.б це многочлени виду f(x)≡a0, a0≠0, a0 є K. Говорять, що многочлен f(x)=0 взагалі немає степеня. Запис многочлена у вигляді (1) назив. канонічним або стандартним. Множину всіх многочленів над областю цілісності К прийнято позначати К[х], а над полем Р - Р[х].
Не нульові многочлени
f(x)=anxn+…+a1x+a0 та g(x)= bnxn+…+b1x+b0 назив. рівними, якщо вони мають одинакові коефіцієнти при відповідних степенях.
Сумою многочленів f(x) та g(x) називається многочлен f(x)+g(x)=Cnxn+…+C1x+C0, де Ci=ai+bi (i=0…n), коефіцієнти якого є сумами коефіцієнтів многочленів що стоять при однакових степенях, а степінь дорівнює n, якщо deg f(x)<deg g(x), і не перевищую n, якщо degf(x)=degg(x)
Добутком многочленів f(x) та g(x) називається многочлен
f(x)*g(x)=Cn+mxn+m+…+C1x+C0 степінь якого дорівнює сумі степенів f(x) та g(x), якщо f(x)≠0 і g(x)≠0, а коефіцієнти Сі є сумами добутків тих елементів многочленів f(x) та g(x) які в сумі дають і. З означення випливає, що якщо хоча б один з многочленів нульовий, то добуток дорівнює нулю.
Говорять, що многочлен f(x) ділиться націло на g(x), g(x)≠0, якщо існує q(x) є Р[х] таке, що f(x)= g(x) q(x)
Спільним дільником многочленів f(x) та g(x) є Р[х] називають многочлен D(x), такий що f(x)÷D(x)та g(x)÷D(x)
Найбільшим спільним дільником многочленів f(x) та g(x) називається такий їх спільний дільник, який ділиться на будь-який інший спільний дільник d(x)=(f(x), g(x)). НСД многочленів визначається однозначно Справді, нехай d(x) та d1(x) – НСД f(x) та g(x), тоді за означенням d(x) ÷d1(x), d1(x)÷d(x), тому d(x)≈d1(x) або d(x)=Сd1(x). Таким чином, НСД визначається однозначно з точністю до асоційовності.
Наявність ділення з остачею в кільці Р[х] дає можливість знаходити НСД методом послідовного ділення з остачею, тобто за алгоритмом Евкліда
Нехай f(x) та g(x) є Р[х], g(x)≠0 і degf(x)≥ degg(x). Тоді можливі випадки:
1. f(x)÷ g(x) 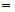 (f(x), g(x))≈ g(x).
(f(x), g(x))≈ g(x).
2. f(x) 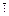 g(x), Розділимо f(x) на g(x) з остачею, g(x) на r1(x) і тд
g(x), Розділимо f(x) на g(x) з остачею, g(x) на r1(x) і тд
f(x)=g(x)q1(x)+r1(x), deg r1<deg g(x)
g(x)=r1(x)q2+r2(x), deg r2<deg r1 v r2 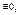
r1(x)=r2(x)q3(x)+r3(x), degr3< 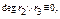
………………………
rn-1(x)=rn(x)qn+1(x)+rn+1(x), 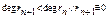
rn(x)=rn+1(x)qn+2(x)
Процес ділення буде скінченим, бо степені остач строго спадають і обмежені знизу нулем. Покажемо, що член rn+1(x) є НСД f(x) та g(x). Справді, піднімаючись знизу вгору легко показати, що rn+1(x)=СД (f(x), g(x)). З іншого боку будь-який СД Д(х) многочленів f(x) та g(x) буде дільником rn+1(x), справді, з 1-го рівняння випливає, що r1(x)÷Д(х), з другого – r2(x)÷Д(х)…, з передостаннього rn-1(x)÷Д(х), тобто rn+1(x) є НСД f(x) та g(x).
При переході від одного ділення до іншого в алгоритмі Евкліда, ділені та дільник можна помножати або ділити на деяке число відмінне від нуля при цьому будуть змінюватися частки, а остачі будуть множитись на деякі числа. Тобто в результаті rn+1(x) буде помножений на деяку константу, яка по суті його не міняє. Тобто процес ділення можна полегшити.
Алгоритм Евкліда дозволяє знайти лінійне представлення 2-х многочленів у кільці Р[х], т.б подати НСД у вигляді
d(x)=f(x)u(x)+g(x)v(x) (2)
де u(x), v(x) є P[x] і залежить лише від часток qi(х). Покажемо, що таке представлення існує. Для цього з передостанньої рівності алгоритма Евкліда виразимо НСД
d(x)=rn+1(x)=rn-1(x)-rn(x)qn+1(x)
з двох попередніх рівностей виразимо rn-1(x) та rn(x)
rn(x)=rn-2(x)-rn-1(x)qn(x)
rn-1(x)=rn-3(x)-rn-2(x)qn-1(x)
та підставимо їх у вираз d(x). Рухаючись угору, та виражаючи остачі одержимо вираз (2) в якому u(x) та v(x) залежать лише від qi(x).
На відміну від знаходження НСД за алгоритмом Евкліда при знаходженні лінійного представлення НСД помножати ділені та дільники на константи неможна, бо від цього суттєво зміняться частки, а значить u(x) та v(x).
Т-ма(лінійне представлення НСД)
Якщо d(x)=(f(x), g(x)), де f(x) та g(x) є Р[х], то в кільці Р[х] знайдуться многочлени u(x), v(x) такі, що має місце представлення
d(x)=f(x)u(x)+g(x)v(x), якщо при цьому deg f(x) >0 і deg g(x)>0 то можна вважати що deg u(x)<deg g(x) i deg v(x)<deg f(x).
Д-ня Існування представлення (2) доведено вище. Покажемо, що справджується друга частина теореми. Припустимо, що це не так і
deg u(x)≥ deg g(x) тоді, розділивши deg u(x) на deg g(x) з остачею одержимо:
u(x)=g(x)q1(x)+r1(x), де degr1(x)<degg(x) або r1(x)≡0 Підставимо u(x) у вираз (2) отримаємо
d(x)=f(x)(g(x)g1(x)+r1(x))+g(x)v(x)
d(x)=f(x)r1(x)+g(x)(f(x)q1(x)+v(x))
Оскільки deg r1(x)<deg g(x) → degr1(x)f(x)<deg f(x)g(x),але в такому випадку степінь другого доданка правої частини більший ніж степінь першого доданку і тому степінь правої частини буде не менший ніж deg f(x)g(x)=deg f(x)+deg g(x)>deg f(x) i deg f(x)g(x)>deg g(x). З іншого боку, степінь d(x) збігається з степенем правої частини і тому більший за degf(x) і більший ніж deg g(x) що неможливо, бо d(x) – дільник f(x) і g(x), т.б припущення невірне. Отже deg u(x)<deg g(x) аналогічно переконуємось що deg v(x)<deg f(x).▲
12. Звідність многочленів над полем. Основна теорема подільності многочленів.
Як відомо, елементи кожного кільця розподілені наступним чином К={0} 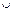 Е
Е 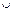 Пр.
Пр. 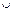 Скл.
Скл.
0 - нульовий елемент
Е – множина оборотних елементів
Пр – множина простих елементів
Скл. – множина складених елементів
Зокрема оборотними елементами кільця Р[х] виступають відмінні від нуля константи поля Р, прості елементи цього кільця прийнято називати незвідними, а складені – звідними.
Многочлен де f(x) є Р[х] додатного степеня називається звідним над полем Р, якщо його можна розкласти в добуток двох многочленів степені яких менші ніж степнь f(x)
f(x) звідний ↔ f(x) = g(x) q(x)
Якщо такого розкладу не існує, то многочлени називаються незвідними над полем Р.
Властивості.
1. Многочлени 1-го степеня є незвідними над будь-яким полем Р.
2. Якщо р(х) – незвідний над полем Р і q(x) та p(x) асоційовані то q(x) – незвідний.
3. Якщо р(х) – незвідний над Р і р(х)÷d(x) → або р(х) та d(x) асоційовані, або d(x)≡const є Р/{0}
Д-ня. Якщо р(х) та d(x) асоційовані, твердження доведено. Нехай р(х) та d(x) не асоційовані, тоді означенням незвідності многочлена d(x)=С, С= const. ▲
4. Якщо р(х) – незвідний і f(x) не ділиться націло на p(x), то (f(x),p(x))=1
5. Якщо р(х) і q(x) незвідні, то р(х) і q(x) або асоційовані, або взаємно прості.
6. Якщо f(x) g(x) ділиться націло на p(x), де p(x) – незвідний над Р, то або f(x)÷ p(x) або g(x)÷p(x)
Д-ня Нехай f(x)÷p(x), тоді твердження доведене. Припустимо, що f(x) не ділиться на p(x) тоді (f(x),p(x))=1. Подальше твердження випливає з властивостей взаємно простих многочленів.
7. Над будь-яким числовим полем Р кількість нормованих незвідних многочленів нескінченна.
Д-ня. Многочлен називають нормованим, якщо його старший коефіцієнт дорівнює 1.
Припустимо супротивне, нехай нормованих незвідних многочленів скінченна кількість р1(х), р2(х), …рs(x) Розглянемо многочлен
g(x)=р1(х)+р2(х)+…+рs(x)+1, degg(x)>0 і g(x) та рі(х) не асоційовані, тому многочлен g(x) звідний. За означенням він має дільник степеня менше ніж deg g(x) Зрозуміло, що серед них будуть незвідні. Проте g(x) не ділиться націло на pi(x) - протиріччя. Отже незвідні многочлени мають властивості аналогічні властивостям простих чисел. ▲
Т-ма. (Основна теорема подільності в кільці многочленів)
Будь-який многочлен f(x) додатного степеня з кільця Р(х) можна розкласти у добуток незвідних множників над полем Р до того ж єдиним способом з точністю до асоційованості та порядку слідування співмножників.
Д-ня Існування. Нехай f(x) – многочлен додатного степеня з кільця Р[х] можливі два випадки: 1) якщо f(x) незвідний, то f(x)= f(x) і є шуканий розклад.
2) Нехай f(x) – звідний над полем Р, тоді його можна представити у вигляді f(x)= g(x)h(x) *
тоді 0< deg g, h< deg f(x). Якщо g(x) і h(x) – незвідні, тоді *- шуканий розклад. У противному випадку процес продовжуємо далі. Так як степені многочленів у добутку строго спадають та обмежені знизу нулем, через декілька кроків одержимо
f(x)= р1(х)*р2(х)*…*рm(x), де рі(х) незвідні над Р.
Єдиність. Нехай існує два представлення
f(x)= р1(х)*р2(х)*…*рm(x) і
f(x)=q1(x)*q2(x)*…*qk(x) де будь-які pi та qj незвідні над Р.
Припустимо, що m <k та прирівняємо праві частини вказаних рівностей
р1(х)*р2(х)*…*рm(x)= q1(x)*q2(x)*…*qk(x) **
Оскільки р1(х) – незвідний і q1(x)*q2(x)*…*qk(x) ділиться націло на р1(х), то за властивістю незвідних многочленів хоча б один з gі(x)ділиться націло на р1(х). Без порушення загальності можна вважати, що g1(x)÷р1(х), тоді g1(x) та р1(х)- асоційовані. Скоротимо ** на р1(х) одержимо
р2(х)*…*рm(x)= С1q2(x)*…*qk(x), С1єР
Міркуючи аналогічно, у правій частині останньої рівності знайдеться многочлен gj(x) який ділиться на р2(х), нехай це буде q2(x), тоді р2(х) і q2(x) –асоційовані і скоротивши на р2(х), одержимо: р3(х)*…*рm(x)= С1С2q3(x)*…*qk(x). На m-му кроці будемо мати: 1= Сqm+1(x)*…*qk(x), СєР. Оскільки qі(x) – незвідні то degqi(x)>0 і тому остання рівність неможлива, тобто припущення невірне. Аналогічно показуємо, що випадок m >k неможливий, тобто m=k і f(x)= р1(х)*р2(х)*…*рm(x) і
f(x)=q1(x)*q2(x)*…*qm(x). Повторюючи попередні міркування при відповідній пере нумерації легко довести, що (р1(х), q1(x)), (р2(х), q2(x)), … (рm(x), qm(x)) асоційовані. Таким чином представлення многочлена у вигляді добутку незвідних однозначне. ▲
Замінимо кожен многочлен рі(х) в одержаному представленні нормованим многочленом, зберемо однакові многочлени у степені та винесемо константи, одержимо розк5лад виду:
f(x)=Cp1α1(x)p2α2(x)…pkαk(x) – цей розклад назив. канонічним представленням многочлена. С=an старший коефіцієнт f(x). Якщо αі=1, то множники pі(x) називаються простими, якщо αі>1, то множники pі(x) називаються кратними, а αі – його кратністю.
13. Многочлени над полем раціональних чисел. Цілі раціональні корені многочленів з цілими коефіцієнтами.
Многочлен f(x)=anxn+an-1xn-1+…+a1x+a0 з цілими коефіцієнтами
deg f(x)≥0 називають примітивним, якщо числа an,an-1…a1,a0 є взаємно простими у сукупності.
Date: 2015-04-23; view: 1066; Нарушение авторских прав