Властивості конгруенції

І. Загальні властивості конгруенцій.

1(рефлексивність) a a(modm) дійсно (a–a)÷m для будь-якого m

2.(транзитивність) Для будь-яких a, b, c є Z, якщо a b(modm), b c(modm), то a c(mod m)

Дійсно, з означення конгруенції випливає a=b+mq, b= c+mt, q,tєZ, підставивши другу рівність в першу маємо a=c+mt+mq= c +m(t+q), а отже за означенням a c(mod m)

3. (симетричність) Для будь-яких a і b єZ з того що a b(modm), випливає, що b a(modm)

Дійсно, оскільки a b(modm), то (a-b)÷m, звідки -(b-a)÷m і (b-a)÷m → b a(modm).

Оскільки виконуються ці три властивості, то відношення конгруентності є відношенням еквівалентності.

4. Кожне число конгруентне зі своєю остачею при діленні на m, тобто якщо a=mq+r, 0≤ r ≤m то a r(modm).

Д-ня випливає з 3) означення конгруентності.

5. Якщо конгруенція має місце по модулю m, то вона має місце і по будь-якому модулю, що є дільником числа m.

З умови маємо (a-b)÷m, нехай d-дільник m, тоді (a-b)÷ d, або a b(mod d).

6. Якщо конгруенція має місце по кількох модулях, то вона має місце і по їх НСК, тобто

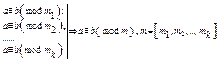
Доведення.

Припустимо, що

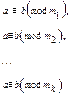
і 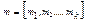- НСК чисел .

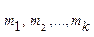З даних конгруенцій випливає, що різниця (a-b) ділиться націло на числа m₁, m₂,…m_k, тому (a-b) повинно ділитися на їх НСК.

Отже, 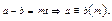Властивість доведено.

ІІ. Властивості конгруенцій, пов’язані з додаванням і відніманням.

1. Дві конгруенції за одним і тим же модулем можна почленно додавати та віднімати.

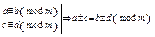
Д-ня. Нехай a b(modm), c d(modm), це означає, що (a-b)÷m, (c-d)÷m, тоді (a-b)+(c-d)÷m, з чого випливає a+c b+d(modm), аналогічно (a-b) - (c-d)÷m, звідки

a-c b-d(modm)

2. До будь-якої частини конгруенції можна додавати або віднімати число кратне модулю т.б. a b(modm)→ a +mt b(modm), a b+mt(modm).

З умови випливає, що a= b+mq, покладемо q=t+q₁ тоді a= b+m(t+q₁) або a=b+mt+mq₁ → a b+mt(modm).

3. До обох частин конгруенції можна додати (відняти) одне й те ж саме ціле число: a b(modm) → a+c b+c(modm)

На основі рефлективності конгруентності число с конгруентне само з собою за будь-яким модулем в тому числі і за m. Конгруенції за однаковим модулем можна почленно додавати з чого випливає властивість.

4. З однієї частини конгруенції в іншу можна перенести число взявши його з протилежним знаком. a+c b(modm)→a b-c(modm)

Використавши 1 і 7 маємо a+c b(modm) -b -b(modm) звідки a b-c(modm).

ІІІ. Властивості конгруенцій, пов’язані з множенням та діленням.

1. Дві конгруенції з одним і тим же модулем можна почленно перемножити

За умовою a=b+mq, c= d+mt, q,tєZ перемноживши рівності дістанемо

ac=bd+m(dq+bt+mqt), перепозначивши маємо ac=bd+mq' або ac bd(modm).

2. Обидві частини конгруенції можна підносити до одного і того ж натурального степеня

Доведення випливає є попередньої властивості: беремо n штук рівних конгруенцій і перемножуємо.

3. Обидві частини конгруенції можна помножити на одне й те ж саме ціле число.

Оскільки a=b+mq то aс=bс+mqс, взявши qс=q' одержимо ac bс(modm).

4. Обидві частини конгруенції і модуль можна скоротити на їх спільний дільник.

Справді, ac bс(modmс)→ ac=bс+(mс)t→ a=b+mt→ a b(modm).

5. Якщо одна частина конгруенції і модуль діляться на деяке число, то і інша частина конгруенції повинна ділитися на це число.

З означення конгруенції випливає: a=b+mq, qєZ або a - mq =b, оскільки a÷k, m÷k → a - mq÷k →b÷k

6. Обидві частини конгруенції і модуль можна скоротити на їх спільний дільник

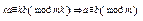
7. Якщо одна частина конгруенції і модуль діляться на деяке число, то і ін. частина конгруенції повинна ділитися на це ж число.

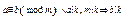
8.

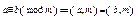
9. 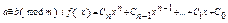-многочлен n-го степеня, 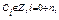то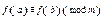

Т-ма (Ейлера)

Якщо (a,m)=1, то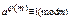

Д-ня. Виберемо будь-яку ЗСЛm (зведену систему лишків) {x₁, x₂, … x_ψ(m)} За властивістю система {аx₁, аx₂, … аx_ψ(m)}, де (а,m)=1 також утворює ЗСЛm. Очевидно, що при відповідній пере нумерації ax₁~x_i1,, ax₂~x_i2, … аx_ψ(m)~ x_ψ(m). Одержимо, що відповідні елементи визначають один і той же клас лишків по модулюm тобто aх₁ х_і1(modm),

ах₂ х_і2(modm),

……………………….

aх_ψ(m) х_іψ(m)(modm).

Перемноживши вказані конгруенції маємо: a^ψ(m) х₁х₂…х_ψ(m)

х_і1х_і2…х_іψ(m)(modm). Оскільки х₁х₂…х_ψ(m)=х_і1х_і2…х_іψ(m) і кожне з чисел х_к взаємно просте з модулем, то скоротивши останню конгруенцію на вказаний добуток одержимо ▲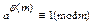

Як наслідок з теореми Ейлера одержимо малу теорему Ферма

Т-ма Якщо p- просте число, і (a,p)=1, то .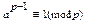

Д-ня. Покладемо в теоремі Ейлера m=p, тоді (a,p)=1 тоді і тільки тоді коли a÷p. Враховуючи, що φ(p)=p-1,та підставляючи цей вираз в теорему Ейлера будемо мати ▲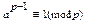

Наслідок Якщо аєZ, p – просте число, то (a^p - a)÷p.

Д-ня.1) Якщо (a,p)=1, то за малою теоремою Ферма 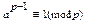помноживши обидві частини на а будемо мати:

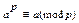звідки (a^p - a)÷p.

2)Нехай (a,p)≠1 →a÷p →(a^p - a)÷p.

9. Функція Ейлера та її властивості. Теорема про мультиплікативність функції Ейлера.

Функція, яка визначає кількість натуральних чисел, що не перевищують даного і взаємно прості з ним називається функцією Ейлера. Позначають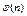

Date: 2015-04-23; view: 1328; Нарушение авторских прав