Наслідки

1. Якщо многочлен f(х) з дійсними коефіцієнтами має комплексний корінь α=a+bi, то його коренем буде і число спряжене до α, = a - bi.

Д-ня. Нехай многочлен

f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ є R має комплексний корінь α. Тобто f(α)=a_nαⁿ+a_n-1α^n-1+…+a₁α+a₀=0.

Візьмемо комплексне спряжене від многочленів останньої рівності

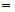
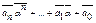=0

=0

а_і – дійсні числа, вони співпадають з своїми спряженими: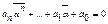

f()=0, тобто - корінь f(х) ▲

2. Якщо многочлен f(х) з дійсними коефіцієнтами має комплексний корінь α кратності к, то він має корінь тієї ж кратності.

3. Над полем дійсних чисел незвідними можуть бути многочлени першого або другого степеня і тільки вони.

Д-ня. Нехай f(х) є незвідним многочленом над дійсним полем. Припустимо, що deg f(х)>2. За лемою 2 наслідком 1 він матиме комплексний корінь α і , тоді f(x)=(x-α)(x- )*g(x) причому

deg g(x) ≥1

f(x)=(x² – αx - x + α )*g(x), або

f(x)=(x² - (α + )x+ α )*g(x), де

(α + ) є R, α є R таким чином многочлен в дужках має дійсні коефіцієнти і враховуючи що deg g(x)≥1 робимо висновок, що f(x) буде незвідним над R ▲

15. Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел

Припущення, що кожен многочлен з числовими коефіцієнтами розкладається в полі комплексних чисел на лінійні множники було висловлено ще в 1629р Жираром. Строге доведення цього факту було запропоновано Карлом Гаусом аж у 1799р а сам факт сьогодні носить назву основної теореми алгебри комплексних чисел.

Лема. Будь-який многочлен f(x) ненульового степеня з дійсними коефіцієнтами має принаймні 1 комплексний корінь.

Д-ня. Нехай deg f(x)=n, тоді n=2^k*q, де k≥0, (q, 2)=1.

Доведемо твердження леми індукцією по к.

1. Нехай к=0, тоді n=q – непарне число, і за лемою1 f(x) має дійсний (комплексний) корінь.

2. Припустимо, що твердження вірне для всіх натуральних чисел менших за к, тобто для многочленів степінь яких ділиться на 2^к-1 і не ділиться на 2^к .

3. Доведемо, що твердження вірне для многочленів степінь яких ділиться на 2^к.

Нехай f(x) такий многочлен тобто

deg f(x) =2^kq=n. У полі розкладу Δ f(x) має корені α₁, α₂,…, α_n. Сконструюємо елемент β_ij виду: α_iα_j+C(α_i+α_j) де C - довільне число єR, i<j. таких елементів буде 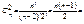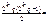2^k-1q(2^kq-1)=2^k-1q₁,

де q₁=q(2^kq-1)-непарне число.

Розглянемо многочлен

φ(х)= 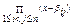, степеня 2^k-1q₁ коренями якого є β_ij тільки вони. Зауважимо, що при перестановках α_k ↔ α_m і навпаки многочлени β_ij не змінюються і тому φ(х) є симетричним відносно α₁, α₂,…, α_n.

Враховуючи, що α₁, α₂,…, α_n корені многочлена з дійсними коефіцієнтами та застосовуючи теорему, яка є наслідком з формули Вієта одержимо, φ(х) також матиме дійсні коефіцієнти. За припущенням індукції (оскільки deg f(x) =2^k-1q₁) многочлен φ(х) з дійсними коефіцієнтами матиме принаймні 1 комплексний корінь β_ijєС Таким чином, для будь-якого дійсного числа С можна вказати пару індексів i та j, (1≤i<j≤n) при яких β_ij=α_iα_j+C(α_i+α_j) є комплексним числом. Зрозуміло також, що різним дійсним числам С₁ і С₂ відповідають різні пари індексів. Проте, оскільки множина дійсних чисел нескінченна, а множина пар (i, j) (таких що1≤i<j≤n) скінченна, то можна вибрати пару чисел С₁ і С₂ (С₁ ≠ С₂), яким відповідатиме одна і та ж пара індексів, тобто

β_ij =α_iα_j+C₁(α_i+α_j)

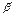_ij = α_iα_j+C2(α_i+α_j)

β_{ij 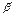ij} – комплексні числа.

Очевидно, що α_i та α_j є коренями квадратного рівняння з комплексними коефіцієнтами

Z² - (α_i + α_j) Z + α_iα_j=0

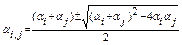Отже α_і та αj є комплексними коренями многочлена f(х) ▲.

Теорема. Будь-який многочлен з числовими (комплексними) коефіцієнтами степінь яких ≥1 має принаймні один комплексний корінь

Д-ня. Нехай многочлен

f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ належить полю комплексних чисел, причому deg f(x) ≥1. Розглянемо многочлен 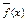= 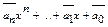коефіцієнти якого є комплексними спряженими до коефіцієнтів f(x). Тоді

f(x) 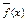=a_n 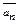х²ⁿ+(a_n +

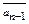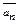+ a_n-1)x^2n-1+…+(a₁ +a₀ )x+ +a₀ має дійсні коефіцієнти. Дійсно a_i 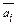=(c+bi)(c-bi)=c²+b² єR

a_k +a_m =(c+bi)(d-li)+(d+li)(c-bi) = cd+bl-cli+bdi+dc-dbi+lci+lb=2(cd+bl) – дійсне число.

(a_k= c+bi, a_m=d+li)

За лемою, многочлен f(x) 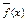має комплексний корінь α, тобто f(α) 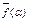=0. В силу цілісності кільця комплексних чисел або f(α)=0 і α – корінь f(х), або 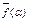=0. Тоді

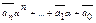=0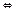

=

.

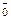
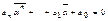Отже є коренем многочлена f(x), тобто многочлен з комплексними коефіцієнтами ненульового степеня має принаймні один комплексний корінь.▲

Date: 2015-04-23; view: 662; Нарушение авторских прав