
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Билинейные и квадратичные формы
|
|
- Определение, матрицы. Теорема Лагранжа. Закон инерции.
- Положительно определенные квадратичные формы. Критерий Сильвестра.
- Приведение квадратичной формы к каноническому (нормальному) виду.
Рекомендуемая литература
Ильин В.А., Позняк Э.Г., Линейная алгебра, М., Наука, 1988.
Беклемишев Д.В., Курс аналитической геометрии и линейной алгебры, М, Наука, 1984.
Канатников А.Н., Крищенко А.П., Линейная алгебра, М., Изд. МГТУ им. Н.Э. Баумана, 1999.
Курош А.Г. Курс высшей алгебры, М., Наука, 1971.
Проскуряков И.В. Сборник задач по линейной алгебре, М., Наука, 1978.
Ефимов А.В., Каракулин А.Ф. и др., Сборник задач по математике для втузов, ч.1, М., Физматлит, 2001
Задание по разделу «Линейная алгебра»
1) Найти размерности и базисы суммы и пересечения подпространств
L1 = < a1, a2, a3 > и L2 = < b1, b2, b3 >, если:
| Вариант 1 | a1 = (1, 2, 1) T | b1= (2, 3, -1) T |
| a2 = (1, 1, -1) T | b2 = (1, 2, 2) T | |
| a3 = (1, 3, 3) T | b3 = (1, 1, - 3) T | |
| Вариант 2 | a1 = (1, 2, 1,-2) T | b1= (1, 1, 1, 1) T |
| a2 = (2,3,1,0) T | b2 = (1, 0,1,-1) T | |
| a3 = (1, 2,2,-3) T | b3 = (1, 3,0, - 4) T | |
| Вариант 3 | a1 = (1, 1,0,0) T | b1= (1,0,1, 0) T |
| a2 = (0,1, 1, 0) T | b2 = (0,2,1,1) T | |
| a3 = (0,0,1,1) T | b3 = (1, 2,1,2) T |
2). Разложить вектор X на суммудвух векторов, один из которых лежит в подпространстве, натянутом на векторы a1, a2, a3, а другой ортогонален к этому подпространству.
| Вариант 1 | X = (-3, 5, 9, 3) T | |
| a1 = (1, 1, 1, 1) T | a2 = (2, - 1, 1, 1) T | a3 = (2, - 7, - 1, - 1) T |
| Вариант 2 | X = (2,- 5, 3,4) T | |
| a1 = (1, 3, 3, 5) T | a2 = (1, 3, -5, -3) T | a3 = (1, -5, 3, - 3) T |
| Вариант 3 | X = (5, 2, - 2, 2) T | |
| a1 = (2, 1, 1, - 1) T | a2 = (1, 1, 3, 0) T |
3) Если линейный оператор φ, действующий в пространстве L n, имеет n линейно независимых собственных векторов e1, e2, … en, соответствующих собственным числам λ1, λ2, …..λn, то в базисе из этих векторов матрица оператора имеет диагональный вид с диагональными элементами, равными собственным числам.
Для заданной матрицы оператора найти этот базис и соответствующую ему диагональную форму матрицы.
| Вариант 1 | Вариант 2 | Вариант 3 |
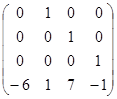
| 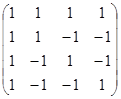
| 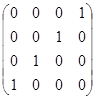
|
4). Линейный оператор φ переводит векторы a1, a2, a3 соответственно в векторы b1, b2, b3.
Найти матрицу оператора φ в том же базисе, в котором заданы координатами все векторы:
| Вариант 1 | a1 = (1, 2, -3) T | a2 = (0, 1, 2) T | a3 = (1, 0, 4) T |
| b1= (1, 1, 1) T | b2 = (1, 2, 1) T | b3 = (0, 1, 1) T | |
| Вариант 2 | a1 = (1, 2, 1) T | a2 = (4, 3, - 2) T | a3 = (- 5, - 4, - 1) T |
| b1= (1, 1, 1) T | b2 = (1, 0, 1) T | b3 = (0, - 1, 1) T | |
| Вариант 3 | a1 = (1, 1, 1) T | a2 = (2, - 3, 1) T | a3 = (4, 1, - 5) T |
| b1= (0, 1, 0) T | b2 = (0, 1, 1) T | b3 = (1, 1, 0) T |
5). Преобразовать к каноническому виду ортогональным преобразованием квадратичную форму и выписать преобразование координат
| Вариант 1 | x12 + 2x22 + 3x32 - 4x1x2 - 4x2x3 |
| Вариант 2 | 3x12 - 8x1x2 - 3 x22 - x32 + 4x3x4 - 4x42 |
| Вариант 3 | 4x12 + 4x1x2 - 12x1x3 - 6x2x3 + x22 + 9x32 |
Date: 2015-04-23; view: 858; Нарушение авторских прав