Властивості простих чисел

1. Якщо р - п.ч і р:а, а≠1, аєN, то а=р

Д-ня За означенням простого числа а може дорівнювати або 1, або р, оскільки за умовою а≠1, то а=р

2. Якщо р, q - п.ч., 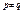, то .

3. якщо ab:p де a, bєN, p-просте число то або a:p, або b:p

Д-ня Справді, кожен із співмножників або взаємно простий з р, або ділиться на р. Але якби всі множники були взаємно прості з р то їх добуток був би взаємно простий з р, тому хоч один з множників ділиться на р.

4. Для довільного натурального а і простого числа р або а:р, або (а,р)=1

Д-ня. Справді, НСД (а,р) як дільник числа р може дорівнювати або р або1. У першому випадку а ділиться на р, у другому- а і р взаємно прості.

5. Найменший неодиничний дільник натурального числа є числом простим.

Д-ня. Нехай а – задумане число, якщо а – просте число, то його найменший дільник який ≠1, =а. Нехай а – складене число, і n₁- його найменший натуральний дільник ≠1. Тоді число можна представити а=n₁а₁, а₁єZ. Припустимо, що n₁- складене число, тоді існує n₂єN, n₂≠1 таке, що n₁::n₂, і n₁≠n₂ у такому випадку число n₂ буде також дільником числа а, меншим за n₁, що суперечить вибору числа n₁, отже n₁- п. ч.

6. Найменший простий дільник складеного числа не перевищує кореня квадратного з цього числа.

Д-ня. Нехай а-складне число, р-його найменший простий дільник. Тоді а=рb, bєZ, р≤ b. Тоді а=рb≥р², р≤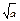

7. Якщо кожне просте число р≤ 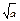не є дільником числа а, то а- просте число.

Теорема Евкліда: Множина простих чисел нескінчена

Доведення: Нехай множина простих чисел скінчена і складається лише з чисел: 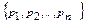. Розглянемо 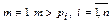, m – складене, а раз так, то воно повинно мати простий дільник, але m не ділиться на жодне з рі, тобто m не може бути складеним, а значить є простим, що суперечить припущенню.

Основна теорема арифметики: кожне відмінне від одиниці натуральне число можна розкласти на добуток простих множників, і до того ж єдиним способом (з точністю до порядку слідування множників).

Д-ня:

1) n - просте то n=n і є шуканий розклад

2) будемо вважати, що n – складене, позначимо через р₁ його найменший не одиничний дільник, тоді n можна розкласти на множники

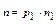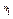, - просте число, якщо - просте число, то це і є шуканий розклад, якщо 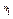- складене, то воно в свою чергу матиме простий дільник р₂ 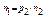, і 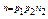. Продовжуючи цей процес далі, в результаті одержимо складну послідовність натуральних чисел 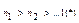цей ланцюг обривається через скінчене число кроків, при цьому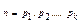

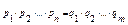Доведемо єдність цього розкладу. Припустимо супротивне: існує ще один розклад , - прості числа., k=m тоді , а отже оскільки ліва частина рівності ділиться на р1, тому на р1 ділиться і права частина, а отже одне з qі=р1, нехай це буде q1. Скоротимо обидві частини рівності на р1, отримаємо, 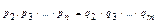повторимо ці міркування для чисел р2, р3, …, рm. Якщо вважати, що m≠s, і наприклад, <s після скорочення одержимо 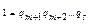. Оскільки q_і натуральні, то 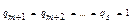, тобто m≥s, аналогічно переконуємося в тому, що випадок s<m неможливий, тому m=s і р₁=q₁, р₂=q₂, … р_m=q_s ▲

Нехай 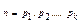. Зберемо в степені однакові множники: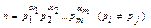 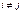, 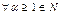канонічний розклад або факторизація цього числа, то всі дільники цього числа мають вигляд:

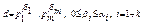
Нехай і

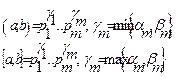
6. Подільність цілих чисел, ділення з остачею.

Нехай a i b - цілі числа, b≠0, говорять, що а ділиться націло на b

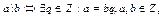
Ділення націло виконується не завжди на Z, проте, якщо виконується, то визначається однозначно

Д-ня. Припустимо, що існує два представлення: а=bq₁ та а=bq₂, q₁, q ₂, єZ віднімемо рівняння, одержимо b(q₁-q₂) =0 Так як b≠0, то q₁-q₂=0 → q₁=q₂ і представлення єдине.

Властивості:

1.

Справді а=а*1, q=1

2. 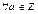, , та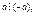

Дійсно, у першому випадку q±а, в другому- q= -1

3.

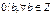
Дійсно, при q=0, маємо вірну рівність 0=b*0

4.

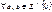
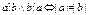
5.

Д-ня. За умовою а=bq1, q1єZ, b=сq2, q2єZ, тоді а=сq´, де q´=q1q2єZ, звідки а:с

6.

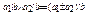
Д-ня. За умовою існують q₁, q₂єZ такі, що а₁=bq₁, а₂=bq₂, додамо ці рівності а₁+а₂=b(q₁+q₂) → а₁+а₂=bq´ (q´=q₁+q₂), а отже а₁+а₂ ділиться націло на b

7.

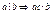
8.

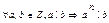
Д-ня. За умовою а=bq, qєZ тоді → аⁿ : b

9. , , ,…

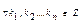
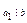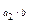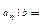
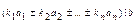
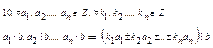
Д-ня випливає з властивостей 6 і 7.

Оскільки в кільці цілих чисел ділення націло виконується не завжди, виникає бажання так узагальнити поняття ділення, щоб воно виконувалося для всіх цілих чисел.

Нехай аєZ, bєN говорять, що а ділиться з остачею на b, якщо існує представлення а=bq+r, причому qєZ, rєZ, 0≤r<b

а – ділене, b – дільник, q – неповна частка, r – остача.

Очевидно, що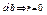

Теорема (про ділення з остачею):

Для довільного цілого а та натурального b ділення з остачею існує і однозначне.

Д-ня.

1. Існування.

Розглянемо 3 можливі випадки в залежності від а.

І) а=0 тоді візьмемо bєN, q=r=0, 0=b*0+0

ІІ) а>0 Якщо 0<а<b, то а=b*0+а, q=0, а=r 0≤r<b.

При а≥b розглянемо ряд чисел b, 2b, 3b, …, kb, … Очевидно, що можна вказати таке число kєN, що kb≤а, (k+1)>а, позначимо це k через q тоді qb≤а≤(q+1)віднімемо від всіх частин рівності qb будемо мати 0≤а-qb<b позначимо а-qb=r, тоді а=qb+r і 0≤r<b

ІІІ) а<0 тоді -а>0 і за попереднім пунктом –а=bq´+r´, 0≤r´<b помножимо останню рівність на -1. а=-bq´-r´, а=b(-q´)+(-r)

Якщо r´=0, то q=-q´, r=-r´=0 і а=bq+0

Якщо r´≠0, то у правій частині рівності (*) додамо та віднімемо b. а=b(-q´)+b-b-r´=

=b(-q´-1)+(b-r´) покладемо q=-q´-1 та r=b-r´ тоді остання рівність матиме вигляд а=bq+r.

Оскільки 0≤r´<b /*-1

0≥-r´>-b /+b

b≥b-r´>0 b≥r>0. Оскільки r´≠0, то 0<r<b або 0≤r<b

2.Єдиність.

Припустимо, що існує два представлення а=bq1+r1 0≤r1<b

а=bq2+r2 0≤r2<b Віднявши рівності маємо

0=b(q1-q2)+(r1-r2), b(q1-q2)=r2-r1

Оскільки ліва частина рівності ділиться на b, то і права ділиться на b. Враховуючи, що r1<b та r2<b тому (r2-r1)<b, отже r2-r1=0, звідки r1=r2, тоді b(q1-q2)=0, а оскільки b≠0 то q1-q2=0, q1=q2 і представлення єдине. Теорему доведено.

Date: 2015-04-23; view: 1146; Нарушение авторских прав