Группа аффинных преобразований, её подгруппы. Эрлангенская программа Ф. Клейна

Множество А всех аффинных преобразований плоскости является группой относительно композиции преобразований. Основным инвариантом этой группы является простое отношение трех точек прямой.

Фигуры 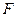и называются аффинно-эквивалентными, если они эквивалентны относительно группы аффинных преобразований. Примерами аффинно-эквивалентных фигур являются любые два треугольника, любые два эллипса, две гиперболы, две параболы.

Примерами подгрупп группы А аффинных преобразований являются:

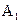· – множество всех аффинных преобразований первого рода. К инвариантам группы А добавляется еще один инвариант – ориентация плоскости.

· Р – группа подобий. К инвариантам группы А добавляется инвариант – величина угла.

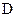· – группа движений. К инвариантам группы подобий добавляется инвариант – расстояние.

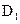· – группа движений первого рода. К инвариантам группы движений добавляется инвариант – ориентация плоскости.

Приведите ещё примеры подгрупп группы А и отметьте изменения в числе инвариантов.

Можно заметить, что чем уже группа, тем шире список инвариантов.

XIX век явился периодом бурного развития геометрических учений. Еще в начале этого столетия было распространено глубокое убеждение в уникальности евклидовой геометрии, так что выражение «геометрия» полностью отождествлялось с понятием «евклидова геометрия». Однако к рубежу 20-х, 30-х годов появляются первые работы Н.И. Лобачевского, Я. Бойяи, посвященные гиперболической геометрии. В конце 60-х годов была опубликована замечательная речь Римана, постулирующая равноправность трех «геометрий постоянной кривизны»: евклидовой, гиперболической и эллиптической.

Бурное развитие геометрии поставило на повестку дня вопрос об общем описании всех рассматриваемых математиками «геометрических систем».

В 1872 году 23-летний Феликс Клейн, вступая в должность профессора кафедры математики Эрлангенского университета, прочел открытую лекцию на тему «Сравнительное обозрение новейших геометрических исследований». Лекция Клейна за ясность позиции автора и открываемые широкие горизонты дальнейшего прогресса геометрии почти сразу получила в научном мире почетное звание «Эрлангенская программа». Идея Клейна состоит в следующем:

Каждой группе преобразований соответствует своя геометрия – теория, которая изучает свойства фигур, сохраняющиеся при всех преобразованиях данной группы.

Таким образом, имеем многообразие геометрий: аффинная геометрия, соответствующая группе аффинных преобразований, геометрия движений, геометрия подобий и т. д.

Date: 2015-05-04; view: 1171; Нарушение авторских прав