
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. З а д а ч а 10. Найти радиус шестой зоны Френеля для волновой поверхности, удаленной на расстояние 15 м от точечного источника монохроматического света с
|
|
З а д а ч а 10. Найти радиус шестой зоны Френеля для волновой поверхности, удаленной на расстояние 15 м от точечного источника монохроматического света с длиной волны 650 нм, если точка наблюдения находится на расстоянии 24 м от поверхности.
Дано:
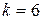 ; ;
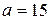 м; м;
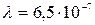 м; м;
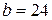 м.
Найти: м.
Найти: 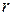 . .
| Решение.
Так как 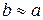 , радиус зоны Френеля (см. рис. 11) вычисляется подстановкой численных данных в формулу (36): , радиус зоны Френеля (см. рис. 11) вычисляется подстановкой численных данных в формулу (36): 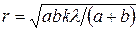 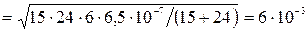 м.
Ответ: м.
Ответ: 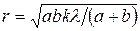 , , 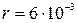 м. м.
|
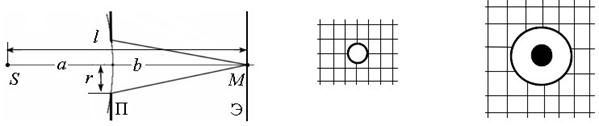
З а д а ч а 11. Экран Э (рис. 12)для наблюдения дифракции Френеля находится на расстоянии 12 м от точечного монохроматического источника света с длиной волны 720 нм. На расстоянии 5 м от источника S помещена преграда с диафрагмой П. При каком радиусе отверстия диафрагмы центр дифракционного изображения отверстия M будет а) наиболее темным, б) наиболее светлым?
Дано:
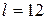 м; м;
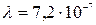 м; м;
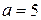 м;
а) м;
а) 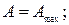 б)
б) 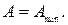 Найти:
Найти: 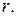
| Решение.
а) Наиболее светлое пятно в центре дифракционного изображения отверстия на экране (рис. 13, а) – следствие наименьшей из всех возможных амплитуд результирующей волны, приходящей в центр изображения. Согласно формуле (39) максимум амплитуды результирующей волны наблюдается при нечетном числе открытых отверстием зон Френеля 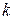 : :
|
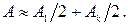 Следовательно, чем светлее центр дифракционного изображения отверстия на экране, тем больше сумма амплитуд в правой части формулы (39). Согласно формуле (35) амплитуда волн, приходящих в точку наблюдения от зон Френеля, убывает с ростом номера зоны. Следовательно, чем больше сумма амплитуд, тем больше амплитуда волны, приходящей от последней (
Следовательно, чем светлее центр дифракционного изображения отверстия на экране, тем больше сумма амплитуд в правой части формулы (39). Согласно формуле (35) амплитуда волн, приходящих в точку наблюдения от зон Френеля, убывает с ростом номера зоны. Следовательно, чем больше сумма амплитуд, тем больше амплитуда волны, приходящей от последней (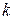 -той) открытой зоны. Но среди волн, приходящих от зон с нечетными номерами, максимальную амплитуду имеет волна, приходящая от первой зоны Френеля. Таким образом, в данном случае
-той) открытой зоны. Но среди волн, приходящих от зон с нечетными номерами, максимальную амплитуду имеет волна, приходящая от первой зоны Френеля. Таким образом, в данном случае 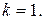 Так как
Так как  радиус отверстия (рис. 12) вычисляется по формуле (36) при
радиус отверстия (рис. 12) вычисляется по формуле (36) при 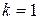 , в которой
, в которой 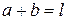 и
и 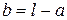 :
: 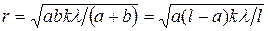 . Подставив сюда численные данные, получим:
. Подставив сюда численные данные, получим: 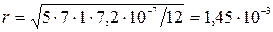 м.
м.
а б
Рис. 12 Рис. 13
б) Наиболее темное пятно в центре дифракционного изображения отверстия на экране (рис. 13, б) – следствие наименьшей из всех возможных амплитуд результирующей волны, приходящей в центр изображения. Согласно формуле (38) минимум амплитуды результирующей волны наблюдается при четном числе открытых отверстием зон Френеля 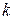 :
: 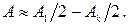 Следовательно, чем темнее центр дифракционного изображения отверстия на экране, тем меньше разность амплитуд в правой части формулы (38). Согласно формуле (35) амплитуда волн, приходящих в точку наблюдения от зон Френеля, убывает с ростом номера зоны. Следовательно, чем меньше разность амплитуд, тем больше амплитуда волны, приходящей от последней (
Следовательно, чем темнее центр дифракционного изображения отверстия на экране, тем меньше разность амплитуд в правой части формулы (38). Согласно формуле (35) амплитуда волн, приходящих в точку наблюдения от зон Френеля, убывает с ростом номера зоны. Следовательно, чем меньше разность амплитуд, тем больше амплитуда волны, приходящей от последней (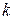 -той) открытой зоны. Но среди волн, приходящих от зон с четными номерами, максимальную амплитуду имеет волна, приходящая от второй зоны Френеля. Таким образом, в данном случае
-той) открытой зоны. Но среди волн, приходящих от зон с четными номерами, максимальную амплитуду имеет волна, приходящая от второй зоны Френеля. Таким образом, в данном случае 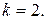 Так как
Так как  радиус отверстия вычисляется по формуле (36) при
радиус отверстия вычисляется по формуле (36) при 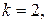 в которой
в которой 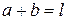 и
и 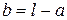 :
: 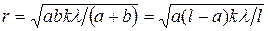 . Подставив сюда данные, получим:
. Подставив сюда данные, получим: 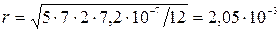 м.
м.
Ответ: а) 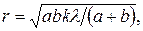
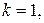
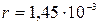 м;
м;
б) 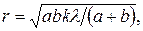
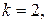
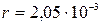 м.
м.
З а д а ч а 12. На непрозрачную преграду с отверстием радиусом 1 мм падает плоская монохроматическая волна. Когда расстояние от преграды до установленного за ней экрана равно 0,381 м, в центре дифракционной картины наблюдается резкий минимум интенсивности. При удалении экрана до расстояния 0,508 м минимум интенсивности сменяется резким максимумом. Определить длину волны падающего света и число зон Френеля, открывавшихся отверстием при первом положении экрана.
Дано:
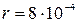 м; м;
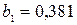 м; м;
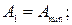
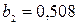 м; м;
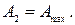 Найти:
Найти: 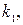 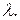
| Решение.
Так как падающая на преграду П волна плоская (рис. 14), для радиуса отверстия в обоих положениях экрана Э справедлива формула (37):
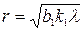 ; (40) ; (40)
|
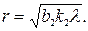 (41)
(41)
В формулах (40) и (41)  и
и 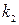 – число открываемых отверстием зон Френеля при первом и втором положениях экрана соответственно. Установим связь между ними. Согласно формулам (40) и (41) при возрастании расстояния до преграды (
– число открываемых отверстием зон Френеля при первом и втором положениях экрана соответственно. Установим связь между ними. Согласно формулам (40) и (41) при возрастании расстояния до преграды (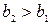 ) и постоянстве радиуса отверстия и длины волны число открытых зон уменьшается:
) и постоянстве радиуса отверстия и длины волны число открытых зон уменьшается: 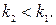 Так как минимум сменяется максимумом один раз,
Так как минимум сменяется максимумом один раз,  и
и 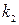 отличаются на 1:
отличаются на 1: 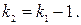 Подставим это равенство в формулу (41), а из полученного соотношения выразим
Подставим это равенство в формулу (41), а из полученного соотношения выразим  :
:
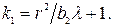 (42)
(42)
Выразим  из формулы (40):
из формулы (40):
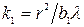 (43) Рис. 14
(43) Рис. 14
и, приравняв правые части соотношений (42) и (43) (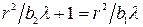 ), найдем длину волны:
), найдем длину волны: 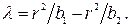 Подставив в это выражение численные данные, получим:
Подставив в это выражение численные данные, получим:  м. Подставив это значение в формулу (43), найдем:
м. Подставив это значение в формулу (43), найдем: 
Ответ: 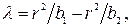
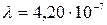 м;
м;

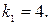
Date: 2015-05-04; view: 1099; Нарушение авторских прав