Контрольная работа №2

2-1. Сколько молекул газа находится в сосуде емкостью 15 л при нормальных условиях?

2-2. Сколько киломолей и молекул содержится в сосуде емкостью 250 см³, если газ находится в нем при давлении 566 мм.рт.ст. и температуре 10°С?

2-3. В сосуде емкостью 40 л находится гелий при температуре 24°С. Произошла утечка газа и давление в нем снизилось на 2 атм.Какое количество газа было потеряно? Температуру газа считать постоянной.

2-4. Каков молекулярный вес газа, если он при температуре 27°С и давлении 2 атм имеет плотность, равную 2,6 г/л?

2-5. В закрытом сосуде емкостью 2 м³ находятся 1,4 кг азота и 2 кг кислорода. Определить температуру газовой смеси, если давление смеси равно 1,4×10⁵ Н/м ².

2-6. Какой объем занимает смесь 1 кг кислорода и 2 кг гелия при нормальных условиях?

2-7. Баллон емкостью 20 л содержит смесь азота и гелия при тем­пературе 47°С и давлении 15 атм. Определить массу как азота, так и гелия, если их общая масса равна 250 г.

2-8. Воздух состоит из 76% азота, 23% кислорода и 1% аргона. Определить кажущийся или средний молекулярный вес воздуха. Молекулярный вес аргона 40 г/моль.

2-9. Определить температуру газа, если средняя кинетическая энергия поступательного движения одной молекулы равна 6,9 ´10^-21 Дж.

2-10. Средняя кинетическая энергия поступательного движения отдельных молекул газа равна 5×10^-14 эрг, число молекул в 1 см³составляет 3×10¹⁹. Определить давление газа.

2-11. Баллон объемом 0,1 м³ содержит 150 г кислорода при давлении 1,25 атм. Определить суммарную кинетическую энергию поступательного движения молекул газа в джоулях.

2-12. Определить среднюю кинетическую энергию поступательного и вращательного движения одной молекулы водяного пара при температуре 150° С.

2-13. Сколько молекул содержится в 1 см³ газа, при давлении 10^-5 мм.рт.ст. и температуре 15°С?

2-14. Определить число Лошмидта, т. е. число молекул, содержащихся в 1 см³ при нормальных условиях.

2-15. В колбе емкостью 200 см³ находится газ при температуре 47°С. Из-за утечки газа из колбы просочилось 10²¹ молекул. На сколько снизится давление в колбе (в мм.рт.ст.)?

2-16. Определить давление, оказываемое водородом на стенки со­суда, если средняя арифметическая скорость молекул газа 1850 м/си в 1 см³ находится 3×10²⁰ молекул.

2-17. При какой температуре молекулы кислорода имеют такую же среднюю квадратичную скорость, как и молекулы азота при t=7⁰ С?

2-18. Баллон емкостью 8 л содержит 2 кг газа при давлении 5 атм. Определить среднюю квадратичную, среднюю арифметическую и наиболее вероятную скорости молекул газа.

2-19. В воздухе при t = 27°С находятся молекулы водорода и взве­шенные мельчайшие пылинки массой 10 ^-8 г. Определить среднюю квадратичную скорость молекул водорода и пылинок, а также их среднюю Кинетическую энергию поступательного движения.

2-20. Определить среднюю длину свободного пробега молекул, если в сосуде емкостью 5 л находится 1 г кислорода.

2-21. Определить среднюю длину свободного пробега молекул азо­та, если плотность разреженного газа 1,8×10 ^-6 кг/м³.

2-22. Определить коэффициент диффузии и коэффициент теплопроводности водорода, находящегося при температуре 0°С и давле­ний 760 мм.рт.ст.

2-23. Сколько соударений в секунду в среднем испытывают, молекулы азота при температуре 0 °С и давлении 760 мм рт. ст.

2-24. Подсчитать молярные и удельные теплоемкости C _ри C _vуглекислого газа, считая его идеальным газом.

2-25. Определить молярные и удельные теплоемкости С _р и С _v кислорода, считая его идеальным газом.

2-26. Масса кислорода,100 г. При постоянном давлении он был нагрет на 30°. Определить работу расширения газа.

2-27. Определить работу расширения 1 кмоль азота, если ему передано 1000 Дж тепла и он расширяется при постоянном давлении.

2-28. Какое количество тепла необходимо подвести к системе, чтобы нагреть 220 г углекислого газа на 20°: а) при постоянном объеме; б) при постоянном давлении?

2-29. При расширении 1 кмоль кислорода была совершена работа в 1000 Дж. Рассчитайте тепловые затраты при изотермическом и изобарическом процессах. Почему при изотермическом расширении газа на ту же работу затрачивается меньшее количество тепла?

2-30. Семь граммов азота при температуре 37° С расширили до тройного объема. Определить работу расширения газа при изотермическом и адиабатическом процессах.

2-31. Сколько выделится тепла, если кислород, занимающий объем 16 л при давлении 5 атм, сжать до объема, равного 4 л. Изотермически, изобарически? Почему в одном случае тепла выделится больше?

2-32. Кислород, находящийся под давлением 100 атм, адиабатически расширился, так, что его объем увеличился в 16 раз. Определить давление кислорода после расширения.

2-33. Определить изменение энтропии 4 кг расплавленного свинца, взятого при температуре плавления, при охлаждении до 0°С? (t_пл =327°С).

2-34. Определить прирост энтропии при превращении 100 г льда при t = -30°С в пар.

2-35. В результате изобарического расширения объем 5 г водорода увеличился с 5 до 10 л. Определить изменение энтропии газа.

2-36. Определить работу идеальной тепловой машины за один цикл, если она в течение цикла получает от нагревателя 500 кал тепла. Температура нагревателя 400° К, температура холодильника 300⁰К.

2-37. Температура нагревателя тепловой машины, работающей по циклу Карно, 207⁰С, а температура холодильника 117°С. Какова должна быть температура нагревателя (при неизменной температуре холодильника), чтобы К.П.Д. машины увеличился в 3 раза?

2-38. За счет каждой килокалории тепла, полученной от нагревателя тепловой машины, работающей по циклу Карно, машина совершает работу, равную 1700 Дж. Определить температуру нагревателя и тепловой, машины, если температура охладителя равна 280° К.

2-39. В цилиндре под поршнем находится газовая смесь, воспламеняющаяся при температуре 927° С. Смесь быстро сжимается до воспламенения. Во сколько раз нужно уменьшить объем смеси, чтобы она воспламенилась, если начальная температура смеси 27° С? Считать процесс адиабатическим и k =1,5.

2-40. Найти постоянные а и b в уравнении Ван-дер-Ваальса для углекислого газа и их наименование, если для него Т_к равно 304 К и р_к равно 73 атм.

2-41. Один моль гелия занимает объем 2 л при температуре 27⁰С. Определить давление гелия, пользуясь уравнением Ван-дер-Ваальса. Для гелия критическая температура 5,2 К и критическое давление 2,25 атм.

2-42. Критическая температура для воды 374,3 К, критическое давление 2256 Н/см². Написать уравнение Ван-дер-Ваальса для водяного пара.

2-43. В одной и той же капиллярной трубке вода поднимается на 50 мм, а керосин на 26 мм. Определить коэффициент поверхностного натяжения керосина. Коэффициент поверхностного натяжения воды 0,071 Н/м.

2-44. Спирт, коэффициент поверхностного натяжения которого 0,022 Н/м налит в U-образную трубку. Определить разность диаметров каналов в коленах трубки, если разность уровней спирта составляет 1 см. Плотность спирта равна 800 кг/м³.

2-45. На какую высоту поднимается вода между двумя плоскопараллельными стеклянными пластинками, если расстояние между ними равно 1 мм? Коэффициент поверхностного натяжения воды равен 0,071 Н/м.

2-46. Объем 24 капель воды, вытекающей из капиллярной трубки, равен 1см³. Определить диаметр отверстия трубки, зная, что диаметр шейки капли и диаметр отверстия трубки одинаковы. Коэффициент поверхностного натяжения воды равен 0,071 Н/м.

2-47. U-образный сосуд налита ртуть, плотность которой при 20⁰С равна 13,6 г/см³. Колена сосуда представляют собой капилляры с диаметрами 0,1 и 1,0 мм. Разность уровней ртути составляет 15 см. Найти коэффициент поверхностного натяжения ртути.

2-48. Определить 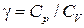и молекулярный вес газа, если скорость распространения звука равна 333 м/с, а средняя квадратичная скорость движения молекул газа равна 484,5 м/с при t=0⁰С.

2-49. Определить 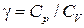, если скорость распространения звука в газе при нормальном давлении 1260 м/с, а плотность его равна 0,09 кг/м³.

2-50. Зная скорость звука в гелии 968 м/с, вычислить скорость звука в водороде при той же температуре.

Розв‘язування кінематичних задач по темі: “Кінематика поступального, криволінійного та обертального руху матеріальної точки.”

Задача 1 Із точки з координатами x ₀, y ₀ кинуто тіло під кутом a₀ до горизонту з початковою швідкістю . Знайти:

1. положення і швидкість тіла через час t;

2. рівняння траєкторії польоту тіла ;

3. нормальне і тангенціальне прискорення тіла;

4. радіус кривизни траєкторії в момент часу t;

5. повний час польоту;

6. найбільшу висоту підйому;

7. кут, під яким треба кинути тіло, щоб висота його підйому дорівнювала далекості польоту (при умові, що );

8. найбільшу далекість польоту;

Направимо осі X iY вздовж горизонтального та вертикального переміщення точки. Векторні рівняння руху тіла:

Для знаходження положення тіла в момент часу t знайдемо проекції на осі координат:

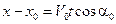
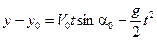
Якщо спроектувати друге векторне рівняння на осі координат, можна знайти складові швидкості:

Тоді результуюча швидкість .

Тангенс кута між напрямком результуючої швидкості та вісі X дорівнює

, тобто він змінюється протягом часу t. Це й зрозуміло, оскільки швидкість геометрично характеризується нахилом дотичної до траєкторії польоту

Щоб визначити тангенціальне та нормальне прискорення тіла в точці з координатами x, y замітимо, що повне прискорення тіла весь час направлено вниз і являє собою прискорення сили тяжіння .

Тангенціальне прискорення дорівнює проекції вектора на дотичну до траєкторії (тобто , що видно з рисунку), а нормальне прискорення дорівнює проекції – на нормаль, тобто

; , то ,

Знайдемо приблизне значення радіуса кривизни (R) траєкторії в момент часу t. Приймаючи, що точка рухається по дузі кола, скористуємося формулою , звідки .

Найбільшу далекість польоту знайдемо за умови . Якщо в рівнянні траєкторії прийняти , то одержамо квадратне рівняння, з якого можна знайти : . Якщо тіло кинуте з точки на поверхні де і , то задача значно спрощується. Скорочуючи на , знаходимо, що . Загальний час польоту можна визначити із формули при , звідки

Найбільшої висоти підйому тіло досягає в момент часу t, коли . Враховуючи що складова швидкості вздовж осі Y дорівнює , то при : .

Тепер скористаємося рівнянням проекції положення тіла на вісь Y, прийнявши : . Виключаючи t з обох рівнянь, одержимо . Очевидно що найбільша висота підйому буде при , тобто коли тіло кинуте вертикально вгору.

Прирівнявши та один одному (при умові, що , ), одержимо

, звідки ;

Знайдемо швидкість тіла в момент приземлення (при умові, що , ).

Для цього підставимо значення 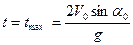у виразі для швидкостей та , а також у формулу для кута між і віссю X.

При цьому одержимо: ; ; ;

Ми бачимо, що вертикальна складова швидкості тіла протягом часу польоту змінюється від до нуля, а потім до . Горизонтальна складова залишається сталою і дорівнює . Таким чином модуль швидкості в польоті весь час змінюється. Змінюється також і напрямок швидкості, в зв‘язку з тим що кута між і віссю X зменшується від до нуля (в точці максимального підйому) і потім до (в точці приземлення).

Date: 2015-11-15; view: 1787; Нарушение авторских прав