Работа электростатического поля

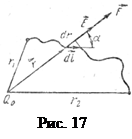
Вычислим работу по перемещению пробного заряда Q в поле точечного заряда Q ₀ (рис.17). Для определенности возьмем 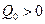и 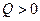и спроектируем перемещение на направление радиус-вектора :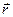

;

; ;

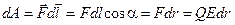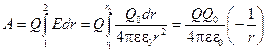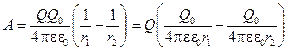Получаем:

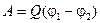, где 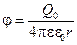– характеристика данной точки поля.

Если начало и конец пути совпадают, то

,

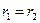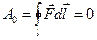
т. е. поле точечного заряда потенциально. Любой заряд представляет собой совокупность достаточно малых заряженных частей, следовательно, по принципу суперпозиции полей, поле такого заряда есть суперпозиция полей точечных зарядов. Таким образом, электростатическое поле любого заряда (зарядов) является потенциальным полем:

,

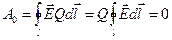т. е. циркуляция вектора напряженности 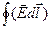электростатического поля равна нулю.

Если бы по одной силовой линии, двигаясь в одну сторону, можно было вернуться в исходную точку (т. е. обойти замкнутую кривую), то циркуляция вектора была бы не равна нулю (поле не потенциально), так как 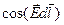был бы одного знака и отличен от нуля. То, что циркуляция в потенциальном поле равна нулю, доказывает, что по одной силовой линии нельзя обойти замкнутый контур, т. е. силовые линии разрывны. Данное выражение является необходимым и достаточным условием потенциальности поля.

Поле совершило работу по переносу заряда Q из одной точки в другую. Следовательно, потенциальная энергия системы зарядов Q ₀, Q в первом состоянии больше, чем во втором, на величину А. Обозначив энергию в этих состояниях через W ₁ и W ₂, получаем:

.

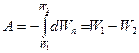Сравнивая эту формулу с выражением для работы, имеем: ; 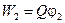. Следовательно, в произвольной точке поля величина, измеряемая потенциальной энергией, приходящейся на единичный положительный пробный заряд, помещенный в данную точку поля, называется потенциалом электростатического поля в этой точке. В частности, значение потенциала поля точечного заряда 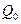на расстоянии 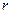от него можно определить следующим образом:

.

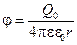Потенциал точки поля произвольного заряда (зарядов) можно представить по принципу суперпозиции полей в виде

,

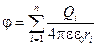где r_i – расстояние от Q_i, до рассматриваемой точки. Разность потенциалов 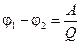,т.е. измеряется работой, которую поле может совершить, перенося единичный положительный заряд из одной точки в другую (А – работа переноса заряда Q между этими точками).

Как всякая потенциальная энергия, потенциал измеряется с точностью до аддитивной постоянной. Обычно за нуль принимают потенциал бесконечно удаленных точек или, в практических измерениях, потенциал Земли.

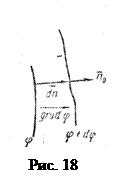
Эквипотенциальной называется поверхность, все точки которой имеют одинаковые потенциалы.

Пусть на рис.18 изображены две эквипотенциальные поверхности, имеющие потенциалы j и j + d j, dn – нормаль к поверхностям. Напряженность поля связана с градиентом потенциала формулой:

.

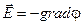Date: 2015-11-15; view: 441; Нарушение авторских прав