
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Індивідуальний комплект
|
|
навчально-методичних матеріалів
з дисципліни: Фізика
частина 1
Студента групи _____________________________________________
Спеціальність_______________________________________
Викладачі: проф. Мочалов О.О.
викл. Коваль С.С.
Рекомендовано методичною Радою ІЗДО,
як методичні вказівки
Миколаїв 2004
Мочалов О.О., Коваль С.С. Індивідуальний комплект навчально-методичних матеріалів з дисципліни "Фізика", частина 1: Методичні вказівки. – Миколаїв; ІЗДО НУК, 2004. – 59 с.
Кафедра Фізики
Приведено скорочену програму курсу, основи теоретичного матеріалу, завдання на практичні заняття та самостійну проробку, перелік та ключ до вибору свого варіанту контрольної роботи, вихідні дані для виконання контрольної роботи та зразок її виконання, перелік контрольних питань на екзамен, перелік основної та додаткової літератури.
© Мочалов О.О., Коваль С.С.
© ТОВ "Університет – НКИ"
Мета викладання дисципліни – забезпечення теоретичної підготовки в різних областях фізичної науки, що дозволяє орієнтуватися у стрімкому потоці науково-технічної інформації на відповідному етапі розвитку суспільства, і яка надає можливості спеціалісту використовувати нові фізичні принципи та розробок у відповідних галузях науки і техніки.
Завдання дисципліни
· вивчення основних фізичних явищ; оволодіння фундаментальними поняттями, законами та теоріями класичної та сучасної фізики, а також засобами фізичного дослідження;
· формування наукового світогляду та сучасного фізичного мислення;
· оволодіння прийомами та засобами рішення конкретних задач з різноманітних областей фізичної науки;
· ознайомлення з сучасною науковою апаратурою, формування навиків проведення фізичного експерименту, вміння виділити конкретний фізичний зміст в прикладних задачах майбутньої спеціальності.
Студент повинен знати основні фізичні явища, що протікають у природі та речовині; фундаментальні закони та теорії класичної і сучасної фізики; методику розв¢язування конкретних фізичних задач; методи фізичного дослідження явищ і законів природи; сучасні наукові прилади; методику проведення експериментів і розрахунку похибок вимірювань.
Студент повинен вміти використовувати фізичні закони для рішення конкретних задач з різних областей фізики; відокремлювати конкретний фізичний зміст у прикладних задачах майбутньої спеціальності; користуватися сучасними науковими приладами; розраховувати похибку фізичних вимірювань.
ПРОГРАМА КУРСУ "ФІЗИКА"
1 частина
Лекция 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ. §1. Перемещение, скорость, ускорение. §2. Тангенциальная и нормальная составляющие ускорения. §3. Связь между векторами линейных и угловых скоростей и ускорений.
Лекция 2. §4. Инерция, масса, импульс. Сила, виды и категории сил в природе. §5. Законы Ньютона, их физическое содержание и взаимосвязь. §6. Инерциальные системы координат. Преобразование координат Галилея. Независимость массы от времени в классической механике. §7. Закон сохранения импульса. Принцип реактивного движения.
Лекция 3. §8. Работа переменной силы. §9. Кинетическая и потенциальная энергии. Энергия упруго деформированного тела. §10. Закон сохранения энергии в механике. Консервативные и диссипативные системы. §11. Понятие абсолютно твердого тела. Вращение твердого тела вокруг неподвижной оси, его момент инерции.
Лекция 4. §12. Основной закон динамики вращательного движения. §13. Кинетическая энергия вращающегося твердого тела. §14. Закон сохранения момента импульса для системы тел. §15. Гироскопический эффект и его применение.
Лекция 5. §16. Гравитационное поле и его напряженность. Понятие потенциала и его градиент. §17. Применение законов сохранения к упругому и неупругому удару. МОЛЕКУЛЯРНАЯ ФИЗИКА ИТЕРМОДИНАМИКА. §18. Термодинамический и молекулярно-кинетический методы изучения тел. Термодинамические параметры. §19. Понятие идеального газа. Основное уравнение молекулярно-кинетической теории газов.
Лекция 6. §20. Средняя энергия молекулы. Молекулярно-кинетическое толкование температуры. §21. Уравнение состояния идеального газа. Смеси газов. §22. Максвелловское распределение молекул по скоростям. §23. Барометрическая формула. Больцмановское распределение частиц в потенциальном поле.
Лекция 7. §24. Эффективный радиус молекулы. Число столкновений и средняя длина свободного пробега. §25. Степени свободы. Распределение энергии по степеням свободы. Внутренняя энергия идеального газа. §26. Первое начало термодинамики и его применение к изопроцессам. §27. Молекулярно-кинетическая теория теплоемкости газов.
Лекция 8. §28. Адиабатический процесс. §29. Работа, совершаемая газом в различных процессах. §30. Явления переноса в газах: диффузия, теплопроводность (вывести), внутреннее трение.
Лекция 9. §31. Круговые, необратимые и обратимые процессы. Принцип действия тепловой и холодильной машин. §32. Идеальная тепловая машина Карно и ее КПД. Абсолютная шкала температур. §33. Энтропия. §34. Второе начало термодинамики и его статистический смысл. Связь энтропии и вероятности состояния.
Лекция 10. §35. Отступление от законов идеальных газов. Силы притяжения и отталкивания у реальных газов. §36. Уравнение Ван-дер-Ваальса и его анализ. Критическое состояние. §37. Внутренняя энергия реального газа.
Лекция 11. §38. Эффект Джоуля-Томсона. Точка инверсии. §39. Сжижение газов, работы П.Л. Капицы. §40. Характеристика жидкого состояния. Поверхностный слой, поверхностное натяжение. Формула Лапласа.
Лекция 12. §41. Явление смачивания. Капиллярные явления. §42.Кристаллические и аморфные тела. Типы кристаллических решеток. §43.Закон Дюлонга и Пти. §44. Условия равновесия фаз в однокомпонентной системе. Диаграмма p – Т. Тройная точка.
Лекция 13. §45. Кривые фазового равновесия. Уравнение Клапейрона-Клаузиуса. Понятие о фазовых переходах 1 и 2 рода. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. §46. Закон сохранения заряда. Закон Кулона. §47. Силовые линии поля. Поток вектора напряженности. §48.Теорема Гаусса. §49. Применение теоремы Гаусса к вычислению напряженности полей (вывести для плоскости и двух плоскостей).
Лекция 14. §50. Работа сил поля при перемещении заряда. Потенциал и методы его измерения. §51. Циркуляция вектора напряженности. Потенциальный характер электростатического поля. §52. Проводники и диэлектрики. Полярные и неполярные диэлектрики. Поляризация ориентационная и деформационная. §53. Вектор поляризации. Напряженность поля диэлектрика. Диэлектрическая проницаемость.
Лекция 15. §54. Электрическое смещение. Теорема Гаусса для поля в диэлектрике. §55. Пьезоэлектрический и электрострикционный эффекты. Сегнетоэлектрики. §56. Электроемкость проводников. Конденсаторы. §57. Энергия заряженного проводника. Энергия электростатического поля.
Лекция 16. §58. Сила тока. Вектор плотности тока. §59. Разность потенциалов, ЭДС и напряжение. §60. Дифференциальная форма закона Ома. §61. Дифференциальная форма закона Джоуля-Ленца.
Лекция 17. §62. Закон Ома для неоднородного участка цепи, для замкнутой цепи. §63. Законы Кирхгофа для разветвленных цепей. §64. Трудности классической теории проводимости. Сверхпроводимость. §65. Работа выхода электрона из металла. Контактная разность потенциалов. §66. Термоэлектричество. §67. Явления Пельтье и Томсона. Применение контактных явлений.
Лекция 18. §68. Термоэлектронная эмиссия и ее практическое применение. §69. Электрический ток в вакууме. Роль объемного заряда. Закон Богуславского-Ленгмюра. §70. Ионизация газа и рекомбинация ионов. Несамостоятельный разряд. §71. Самостоятельный разряд. Полная вольтамперная характеристика газового разряда. Виды разрядов (самостоятельно). §72. Понятие о плазме. Плазма в магнитном поле. Электронные и ионные приборы.
КИНЕМАТИКА
Механическое движение – это перемещение тела или его частей относительно других тел, принимаемых, за неподвижные. С этими телами обычно связывают систему координат (отсчета). Различают поступательное и вращательное движения.
Поступательным называется движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе. Следовательно, траектории всех точек тела одинаковы.
Вращательным называется движение, при котором одна прямая, связанная с телом, остается неподвижной; эта прямая является осью вращения. Траектории всех точек тела суть концентрические окружности, центры которых лежат на оси, а плоскости перпендикулярны к ней. Произвольное движение тела можно представить как совокупность только поступательного и вращательного движений.
Перемещением точки называется вектор  , соединяющий два последовательных положения движущейся точки:
, соединяющий два последовательных положения движущейся точки: 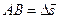 (надо различать путь точки, движущейся по кривой АВ, и перемещение этой точки
(надо различать путь точки, движущейся по кривой АВ, и перемещение этой точки  – рис. 1).
– рис. 1).
 Величина, изменяемая перемещением за единицу времени, называется скоростью и вычисляется как первая производная перемещения по времени:
Величина, изменяемая перемещением за единицу времени, называется скоростью и вычисляется как первая производная перемещения по времени:

Вектор скорости направлен вдоль вектора  (т.е. по касательной к траектории).
(т.е. по касательной к траектории).
Величина, измеряемая изменением вектора скорости за единицу времени, называется ускорением и вычисляется как вторая производная перемещения по времени:
 .
.
Вектор ускорения направлен вдоль вектора изменения скорости (а не вдоль вектора скорости).
При вращательном движении твердого тела различают линейные скорости точек ( ) и угловую скорость тела (
) и угловую скорость тела ( ).
).
Угловая скорость – величина, измеряемая углом поворота радиуса-вектора за единицу времени:
 .
.
где  - единичный вектор (
- единичный вектор ( =1), направленный вдоль оси по правилу правого винта (рис.2).
=1), направленный вдоль оси по правилу правого винта (рис.2).
Угловое ускорение – величина, измеряемая изменением угловой скорости за единицу времени:
 .
.
Вектор углового ускорения направлен вдоль  (а не вдоль
(а не вдоль  ).
).
Вектора линейной и угловой скорости связаны между собой (рис. 3):  , но
, но  , поэтому, учитывая, что
, поэтому, учитывая, что  ,
, 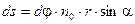 и
и  . Следовательно,
. Следовательно,
 ,
,
где 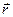 – радиус-вектор данной точки, т. е. вектор, проведенный к этой точке из произвольной точки О, лежащей на оси вращения тела.
– радиус-вектор данной точки, т. е. вектор, проведенный к этой точке из произвольной точки О, лежащей на оси вращения тела.
Дифференцируя по времени последнее выражение, получаем:
 |
 .
.
Но  . Следовательно, линейное ускорение точки тела
. Следовательно, линейное ускорение точки тела
 .
.
Для точек вращающегося тела  . Тангенциальное ускорение
. Тангенциальное ускорение  характеризует изменение линейной скорости по величине. Нормальное ускорение
характеризует изменение линейной скорости по величине. Нормальное ускорение  характеризует изменение скорости по направлению.
характеризует изменение скорости по направлению.
ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Взаимодействие тел приводит к появлению ускорений и деформаций. Мерой такого взаимодействия является сила.
Основной закон динамики (второй закон Ньютона) гласит: изменение импульса абсолютно твердого тела по величине и направлению равно векторной сумме импульса сил, действующих на это тело:
 ,
,
где  – такой малый промежуток времени, в течение которого все силы
– такой малый промежуток времени, в течение которого все силы  можно считать постоянными;
можно считать постоянными;  – импульс силы
– импульс силы  ;
; 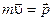 – импульс тела.
– импульс тела.
Если масса тела постоянна, из формулы получаем основное уравнение динамики поступательного движения:
 или
или  .
.
Основной закон динамики применяется к одному телу. Но тело всегда взаимодействует с другими телами, образующими систему тел. Пусть в состав системы входит n тел. К каждому из них можно применить второй закон Ньютона:

где  – равнодействующая сил, действующих на i -е тело;
– равнодействующая сил, действующих на i -е тело;  – импульс этого тела.
– импульс этого тела.
Среди сил, входящих в левую часть этого уравнения, различают силы внутренние и внешние. Внутренними называются силы, действующие на тела системы со стороны других тел этой системы. Внешними называются силы, действующие на тела системы со стороны тел, не входящих в систему. Обозначим буквой  равнодействующую всех внутренних сил, действующих на i -е тело, буквой
равнодействующую всех внутренних сил, действующих на i -е тело, буквой  – равнодействующую всех внешних сил, действующих на это же i -е тело. Тогда
– равнодействующую всех внешних сил, действующих на это же i -е тело. Тогда

Таких уравнений можно написать n. Сложив их почленно, получим:

В этом уравнении сумма внутренних сил равна нулю, так как внутренние силы – это силы взаимодействия, которые, по третьему закону Ньютона, попарно равны и противоположно направлены. Следовательно,
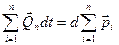 .
.
Геометрическая сумма импульсов всех тел системы называется импульсом этой системы. Уравнение показывает, что импульс системы меняется только под действием импульсов внешних сил. Система тел, для которой векторная сумма внешних сил равна нулю, называется изолированной (при поступательном движении). (Частным случаем такой системы является система, на которую не действуют внешние силы). Для такой системы
 или
или  .
.
Закон сохранения импульса: импульс изолированной системы тел есть величина постоянная. Уравнение можно представить как совокупность трех уравнений для проекций на координатные оси. Если в неизолированной системе удается выбрать такое направление, для которого сумма проекций внешних сил равна нулю, система называется изолированной по данному направлению х:

Таким образом, закон сохранения импульса применим к системе, изолированной по направлению х, в форме:
 .
.
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Рассмотрим движение абсолютно твердого тела, имеющего одну закрепленную точку. Величиной, характеризующей действие силы на такое тело, является момент силы. Моментом силы относительно точки называется векторное произведение радиус-вектора на силу (рис. 4):
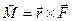
Радиус-вектор силы – вектор, направленный от начала координат (точка, относительно которой рассматривается момент силы) к точке приложения силы. Тело представляет собой совокупность материальных точек. Обозначив равнодействующую сил, действующих на одну из материальных точек, буквой  и умножив уравнение для этой точки слева векторно на
и умножив уравнение для этой точки слева векторно на 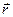 , получим:
, получим:

 или
или  .
.
Вектор  называется моментом импульса материальной точки (относительно выбранного начала координат);
называется моментом импульса материальной точки (относительно выбранного начала координат); 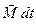 – импульс равнодействующего момента сил, действующих на материальную точку. Написав уравнение для каждой материальной точки тела и сложив почленно все эти уравнения, получим:
– импульс равнодействующего момента сил, действующих на материальную точку. Написав уравнение для каждой материальной точки тела и сложив почленно все эти уравнения, получим:
 .
.
В левой части этого уравнения остается сумма импульсов моментов только внешних (по отношению к телу) сил, действующих на все тело, так как по третьему закону Ньютона сумма моментов внутренних сил равна нулю. Вектор

называется моментом импульса твердого тела (относительно выбранной точки). Выражение позволяет сформулировать основной закон динамики вращательного движения тела с одной закрепленной точкой:
 .
.
Изменение момента импульса абсолютно твердого тела по величине и направлению равно векторной сумме импульсов моментов сил, действующих на это тело. Вектор момента импульса тела относительно точки, вообще говоря, не совпадает по направлению с угловой скоростью. Рассмотрим, например, движение тела, состоящего из двух одинаковых материальных точек (гантель), относительно их центра масс О, если угловая скорость  не перпендикулярна линии, соединяющей эти точки (рис. 5). Предоставленное самому себе тело стремится повернуться так, чтобы вектора момента импульса и угловой скорости совпадали по направлению. Можно показать, что у любого твердого тела есть три таких направления, при вращении вокруг которых вектора
не перпендикулярна линии, соединяющей эти точки (рис. 5). Предоставленное самому себе тело стремится повернуться так, чтобы вектора момента импульса и угловой скорости совпадали по направлению. Можно показать, что у любого твердого тела есть три таких направления, при вращении вокруг которых вектора  и
и  коллинеарные. Эти направления главные оси инерции тела или свободные оси, вокруг которых тело может вращаться долго, будучи предоставлено самому себе.
коллинеарные. Эти направления главные оси инерции тела или свободные оси, вокруг которых тело может вращаться долго, будучи предоставлено самому себе.
Рассмотрим движение тела, имеющего закрепленную ось. Примем за начало координат произвольную точку этой оси О (рис. 6). Спроектируем момент импульса тела

на ось вращения z:

и назовем эту проекцию моментом импульса твердого тела относительно данной оси.
Момент импульса материальной точки  (см. рис. 6). Назовем перпендикуляр к оси
(см. рис. 6). Назовем перпендикуляр к оси  , направленный к данной материальной точке
, направленный к данной материальной точке  , радиусом-вектором этой точки относительно выбранной оси. Принимая во внимание направления векторов, получим:
, радиусом-вектором этой точки относительно выбранной оси. Принимая во внимание направления векторов, получим:
 |
 ;
; 
(так как  , а угол между
, а угол между  и
и  прямой). Величина
прямой). Величина

называется моментом инерции тела относительно данной оси. Здесь  – момент инерции материальной точки
– момент инерции материальной точки  относительно выбранной оси.
относительно выбранной оси.
Выражение тем точнее, чем меньше размеры частей, на которые разбивается данное тело, и чем больше, следовательно, их число n.
Поэтому  или
или  .
.
Момент инерции тела является мерой его инертности во вращательном движении относительно данной оси и зависит от распределения массы тела относительно этой оси.
Мы получили
 .
.
Основной закон динамики вращательного движения проекций на закрепленную ось принимает вид
 .
.
Так как ось вращения закреплена и неподвижна, угловая скорость тела может изменяться только по знаку и величине. Следовательно, сумма проекций на любое направление, перпендикулярное оси вращения моментов всех сил, действующих на тело (включая реакции опор), равна пулю.
В уравнении  – момент i -й силы относительно точки О – можно разложить на три составляющих момента сил
– момент i -й силы относительно точки О – можно разложить на три составляющих момента сил 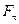 ,
,  и
и  (рис.7). Моменты сил
(рис.7). Моменты сил  и
и  перпендикулярны оси и, как сказано выше, в сумме с другими перпендикулярными составляющими моментов сил равны нулю. Момент тангенциальной составляющей силы
перпендикулярны оси и, как сказано выше, в сумме с другими перпендикулярными составляющими моментов сил равны нулю. Момент тангенциальной составляющей силы 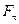 имеет отличную от нуля проекцию на ось вращения
имеет отличную от нуля проекцию на ось вращения  (см. рис. 7):
(см. рис. 7):

 .
.
Моментом произвольной силы относительно выбранной оси называется векторное произведение радиуса-вектора силы относительно этой оси и проекции этой силы на плоскость, перпендикулярную оси:
 .
.
Здесь  – проекция силы
– проекция силы  на плоскость, перпендикулярную оси вращения;
на плоскость, перпендикулярную оси вращения;

Момент силы относительно оси равен проекции на ось вращения момента этой силы относительно точки, лежащей на оси.
Таким образом, в левой части основного закона динамики вращательного движения твердого тела с закрепленной осью написана сумма моментов сил относительно оси вращения.
Если момент инерции относительно оси вращения не меняется, то
 ,
,  и
и  .
.
Мы получили основное уравнение динамики вращательного движения тела вокруг закрепленной оси. В левой части стоит векторная сумма моментов всех сил относительно оси вращения. Основной закон и уравнение динамики вращательного движения применимы к одному телу. Пусть теперь взаимодействуют n тел, образующих систему. Для каждого из тел системы можно написать основной закон в виде
 ,
,
где  и
и  – результирующие моменты внешних и внутренних сил, действующих на i -е тело, относительно выбранной точки;
– результирующие моменты внешних и внутренних сил, действующих на i -е тело, относительно выбранной точки;  – момент импульса этого тела относительно той же точки. Написав это уравнение для каждого тела системы, получим n уравнений. Почленно сложив эти уравнения, будем иметь:
– момент импульса этого тела относительно той же точки. Написав это уравнение для каждого тела системы, получим n уравнений. Почленно сложив эти уравнения, будем иметь:
 .
.
В этом выражении второе слагаемое левой части представляет собой векторную сумму импульсов моментов всех внутренних сил системы, которая, в соответствии с третьим законом Ньютона, равна нулю, так как моменты сил взаимодействия попарно равны и противоположно направлены.
Следовательно, 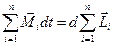 . Обозначим
. Обозначим 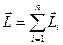 момент импульса системы тел (векторная сумма моментов импульсов всех тел системы). Тогда
момент импульса системы тел (векторная сумма моментов импульсов всех тел системы). Тогда
 .
.
Изменение момента импульса системы по величине и направлению равно векторной сумме импульсов моментов всех внешних сил, действующих на тела этой системы. Изолированной (при вращательном движении) называется система тел, для которой сумма моментов внешних сил равна нулю. В такой системе
 и
и 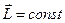
Закон сохранения момента импульса: вектор момента импульса изолированной системы есть величина постоянная (как по модулю, так и по направлению). Как всегда, векторное равенство эквивалентно трем равенствам для проекций на оси координат. Если в неизолированной системе есть такое направление z, для которого 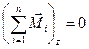 , систему называют изолированной по направлению z. Для такой системы
, систему называют изолированной по направлению z. Для такой системы 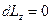 и
и 
РАБОТА
Физическая величина, измеряющая действие силы на определенном пути, называется работой. Элементарная работа силы F на элементе пути dl равна скалярному произведению силы и перемещения:

Как видно, скалярная величина, работа может быть положительной или отрицательной в зависимости от угла между силой F и перемещением dl. При острых углах А >0, тело, действующее силой F, совершает положительную работу. При тупых углах работа тела, действующего силой F, отрицательна. Если угол  равен p/2, работа силы F на перемещении dl равна нулю. Конечная работа силы F при перемещении из точки 1 в точку 2 равна сумме элементарных работ:
равен p/2, работа силы F на перемещении dl равна нулю. Конечная работа силы F при перемещении из точки 1 в точку 2 равна сумме элементарных работ:

Для вращательного движения можно рассчитать аналогично элементарную работу, произведенную силой, лежащей в плоскости вращения при повороте тела на элементарный угол d j:
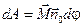 ,
,
где  – момент данной силы относительно оси вращения;
– момент данной силы относительно оси вращения;  — единичный вектор, направленный по оси и связанный с направлением вращения правилом правого винта. Работа силы при повороте тела на конечный угол
— единичный вектор, направленный по оси и связанный с направлением вращения правилом правого винта. Работа силы при повороте тела на конечный угол
 .
.
Силы, работа которых не зависит от формы траектории (зависит лишь от начала и конца пути), называются консервативными. Поле таких сил называется потенциальным. Работа по замкнутому контуру в таком поле равна нулю:
 .
.
Это соотношение является необходимым и достаточным условием потенциальности поля. Расчет работы в поле силы тяготения показывает, что гравитационное поле является потенциальным. Аналогично является потенциальным поле сил упругости. Других типов потенциальных сил в механике нет.
ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ
Наиболее общей мерой различных форм движения материи является ее энергия. Механическая энергия измеряется количеством работы, которую система тел могла бы совершить. Различают два вида механической энергии – кинетическую и потенциальную. Вследствие относительности движения кинетическая энергия относительна, т. е. система обладает различными кинетическими энергиями в разных системах координат. Практически недостижима такая конфигурация системы, при которой ее потенциальная энергия обратилась бы в нуль. Но процессы, происходящие в системе, связаны с переходом ее от одной конфигурации к другой, т. е. с изменением потенциальной энергии, что позволяет принять за нуль потенциальной энергии любое ее значение. Поэтому имеет смысл говорить о потенциальной и кинетической энергии системы тел лишь в выбранной системе координат и при определенном нулевом уровне потенциальной энергии. Если совершают работу внутренние консервативные силы системы, изменяется ее конфигурация (только консервативные силы зависят от взаимного расположения тел системы). Следовательно, потенциальная энергия системы измеряется работой, которую могут совершить ее внутренние консервативные силы.
Переведем систему из какого-то состояния 1 в состояние 2. При этом внутренние консервативные силы совершат работу dA 1,2. При возможном обратном переходе системы в состояние 1 внутренние консервативные силы системы могут совершить работу dA 1,2. Работа этих сил по замкнутому контуру 1–2–1

Но возможная работа внутренних консервативных сил dA 1,2 измеряет потенциальную энергию системы в состоянии 2 (П 2) по отношению к состоянию 1 (П 1), т. е.
 .
.
Таким образом,
 ,
,
где dA – работа внутренних консервативных сил в каком-либо процессе 1–2 (между бесконечно близкими конфигурациями а dП – изменение потенциальной энергии в этом процессе. Например, если консервативнее силы системы совершают отрицательную работу (под внешним воздействием), конфигурация системы изменяется так, что соответственно увеличивается потенциальная энергия системы, и наоборот.
Рассмотрим произвольную систему тел. Для каждого тела этой системы можно написать уравнение движения
 ,
,
где  – равнодействующая всех сил, действующих на i -е тело; mi – масса;
– равнодействующая всех сил, действующих на i -е тело; mi – масса;  – скорость этого тела.
– скорость этого тела.
За время dt i -е тело перемещается на  , Работа, которую
, Работа, которую  совершает на перемещении
совершает на перемещении  , равна
, равна  .
.
Подставив  , получим:
, получим: 
Кинетическая энергия тела 
Ее дифференциал 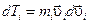
Сравнивая эти выражения, имеем: 
т. е. работа всех сил, действующих на каждое тело системы, равна изменению его кинетической энергии. В частности, если на тело действуют уравновешивающиеся силы,  ,
,  (тело движется равномерно). Не меняется кинетическая энергия тела и в случае перпендикулярности
(тело движется равномерно). Не меняется кинетическая энергия тела и в случае перпендикулярности  и
и  :
:
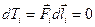
(сила  в этом случае изменяет лишь направление движения, а не величину скорости).
в этом случае изменяет лишь направление движения, а не величину скорости).
Написав уравнение для каждого из n тел системы и почленно сложив эти уравнения, получаем:
 ,
,
где  – кинетическая энергия системы. Изменение кинетической энергии системы тел равно алгебраической сумме работ всех сил, действующих на тела этой системы. Если, например, суммарная работа всех сил равна нулю, кинетическая энергия системы не меняется.
– кинетическая энергия системы. Изменение кинетической энергии системы тел равно алгебраической сумме работ всех сил, действующих на тела этой системы. Если, например, суммарная работа всех сил равна нулю, кинетическая энергия системы не меняется.
Целесообразно из левой части выделить работу внутренних консервативных сил, связанную с изменением потенциальной энергии системы:
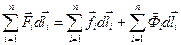 ,
,
где  – внутренние консервативные, а
– внутренние консервативные, а  – все внешние и внутренние диссипативные силы, действующие на тела системы;
– все внешние и внутренние диссипативные силы, действующие на тела системы;
 , или
, или  .
.
Но работа внутренних консервативных сил с обратным знаком равна изменению потенциальной энергии системы за время  :
:
 .
.
Подставив это выражение в последнюю формулу, получим:
 . Итак,
. Итак, 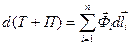 .
.
Изменение полной энергии системы равно работе внутренних диссипативных и всех внешних сил при данном переходе системы из одного состояния в другое.
В частности, для замкнутой консервативной системы тел
 и
и  .
.
Мы получили закон сохранения энергии в механике: полная энергия замкнутой консервативной системы есть величина постоянная.
Мы говорили о системе, тела которой движутся поступательно. Но в общем случае каждое из этих тел может и вращаться. На потенциальной энергии вращательное движение не скажется, а выражение кинетической энергии тела должно быть дополнено.
Кинетическая энергия вращения тела
 ,
,
где J – момент инерции тела относительно данной оси;  - угловая скорость.
- угловая скорость.
Кинетическая энергия тела
 ,
,
где u – скорость поступательного движения оси вращения, относительно которой момент инерции тела J.
Выражения показывают, что энергия системы изменяется только в процессе совершения работы, и количество совершенной работы есть мера переданной энергии (в термодинамике рассматривается другой способ передачи энергии – теплообмен).
ИДЕАЛЬНЫЕ ГАЗЫ
Уравнение состояния идеального газа – уравнение Клапейрона-Менделеева:
 ,
,
где p – давление газа; V – объем, предоставленный массе т газа с молекулярной массой m;
R – универсальная газовая постоянная; Т – абсолютная температура газа.
Основное уравнение кинетической теории газа
 ,
,
где n 0 – концентрация молекул; w k – средняя кинетическая энергия поступательного движения одной молекулы газа. Сопоставляя эти формулы, получаем:
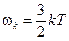 ,
,
где  – постоянная Больцмана (NA – число Авогадро).
– постоянная Больцмана (NA – число Авогадро).
Числом степеней свободы тела i называется число независимых координат, полностью определяющих положение этого тела относительно выбранной системы отсчета.
При поступательном движении молекул существует три независимых направления их движения. Для статистически большого «коллектива» молекул все направления движения равновероятны. Разложив скорости молекул на составляющие вдоль координатных осей, получаем, что средняя кинетическая энергия движения одной молекулы вдоль каждой оси
 .
.
Обычно говорят в этом смысле о средней энергии, приходящейся на одну степень свободы. При увеличении числа степеней свободы (2, 3-атомные молекулы) энергия, приходящаяся на каждую степень свободы, при неизменных условиях остается равной w i, а средняя кинетическая энергия одной молекулы возрастает. При этом соблюдается закон равнораспределения энергий по степеням свободы: кинетическая энергия молекул поровну распределяется между степенями свободы. В соответствии с этим законом, учитывая поступательное и вращательное движение молекул, формулу средней кинетической энергии молекулы надо переписать в виде
 .
.
Внутренней энергией системы тел U называется сумма потенциальных энергий взаимодействия и кинетических энергий микрочастиц этой системы. Для идеального газа
 ,
,
где  – число молекул в массе m газа; m/m – число молей в данной массе газа. Принимая во внимание, что
– число молекул в массе m газа; m/m – число молей в данной массе газа. Принимая во внимание, что  ,
,

 ,
,
В некотором состоянии внутренняя энергия принимает определенное значение  . Если, совершив какой-то процесс, данная масса идеального газа вернется в первоначальное состояние, ее параметры, в том числе температура, примут первоначальные значения. Следовательно, внутренняя энергия примет первоначальное значение U 1, т.е. внутренняя энергия является функцией состояния.
. Если, совершив какой-то процесс, данная масса идеального газа вернется в первоначальное состояние, ее параметры, в том числе температура, примут первоначальные значения. Следовательно, внутренняя энергия примет первоначальное значение U 1, т.е. внутренняя энергия является функцией состояния.
Изменение внутренней энергии определенной массы идеального газа
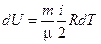 .
.
Если протекает циклический процесс (рис. 8), то
 .
.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Тепловой машиной называется устройство, в котором внутренняя энергия превращается в энергию упорядоченного движения. Внутреннюю энергию можно изменить, либо совершив работу, либо в процессе теплообмена:
 ,
, 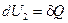 .
.
здесь -d A – работа, совершенная внешними силами над системой; d Q – количество теплоты, сообщенное системе извне. Если оба процесса протекают одновременно, то 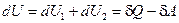 . Известно только два процесса превращения энергии – совершение работы и теплообмен. Поэтому данная формула является наиболее общей записью закона превращения энергии. Таким образом, первое начало термодинамики является законом сохранения и превращения энергии.
. Известно только два процесса превращения энергии – совершение работы и теплообмен. Поэтому данная формула является наиболее общей записью закона превращения энергии. Таким образом, первое начало термодинамики является законом сохранения и превращения энергии.
 .
.
(d A – работа, совершенная системой над внешними телами).
Количество энергии, сообщенной системе в процессе теплообмена, идет на изменение ее внутренней энергии и на совершение системой работы против внешних сил.
Любой процесс можно представить, как совокупность достаточно малых элементов. Так как давление p = F/S, то
 .
.
Следовательно, работа любого процесса  . Этот интеграл графически изображен на рис.8. На этом рисунке показаны два значения работы при изменении объема в одних и тех же пределах. Отсюда ясно, что работа есть функция не только начала и конца процесса, но зависит и от промежуточных точек, через которые идет процесс. Такие функции будем называть функциями процесса (в отличие от функций состояния, зависящих только от начала и конца процесса). Работа по замкнутому циклу может быть не равна нулю. Следовательно, d A в формуле не является полным дифференциалом.
. Этот интеграл графически изображен на рис.8. На этом рисунке показаны два значения работы при изменении объема в одних и тех же пределах. Отсюда ясно, что работа есть функция не только начала и конца процесса, но зависит и от промежуточных точек, через которые идет процесс. Такие функции будем называть функциями процесса (в отличие от функций состояния, зависящих только от начала и конца процесса). Работа по замкнутому циклу может быть не равна нулю. Следовательно, d A в формуле не является полным дифференциалом.
Изменение количества теплоты в калориметрии связано с понятием теплоемкости. Удельная теплоемкость вещества
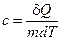 ,
,
где d Q – количество теплоты, необходимое для изменения температуры массы m вещества на dT градусов. Теплоемкость тела  . Молярная теплоемкость вещества – теплоемкость одного моля этого вещества
. Молярная теплоемкость вещества – теплоемкость одного моля этого вещества
 .
.
У газов различают теплоемкости при постоянном объеме (CV – молярная, cV –удельная) и при постоянном давлении (соответственно – Cp, cp).
Подставив выражения для изменения внутренней энергии и работы в первое начало термодинамики, получаем:
 .
.
Вычислим CV. Для этого в формулу теплоемкости подставим последнее выражение, в котором  , так как
, так как  . Получим:
. Получим:
 .
.
Аналогично вычислим Cp, предварительно рассчитав pdV. Для изобарического процесса  . Следовательно,
. Следовательно,
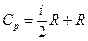 .
.
Сопоставляя выражение для CV и Cp, получаем уравнение Роберта Майера:
 .
.
Отношение  называется коэффициентом Пуассона.
называется коэффициентом Пуассона.
Подставив в отношение g выражение CV и Cp, можно вывести  .
.
Изменение состояния системы (процесс) связано с изменением ее параметров. Для подсчета работы, произведенной при каком-то процессе, необходимо связать между собой непрерывно изменяющиеся параметры системы. В случае произвольного процесса для идеального газа такая связь устанавливается уравнением Клапейрона – Менделеева. В более простых случаях так называемых изопроцессов (когда один из параметров данной массы газа не меняется) эта связь устанавливается газовыми законами: Бойля — Мариотта, Гей-Люссака и Шарля. Эти законы являются частными случаями уравнения состояния идеального газа. Еще один изопроцесс называется адиабатическим. Это процесс, протекающий без теплообмена с окружающей средой:  .
.
Уравнение этого процесса называется уравнением Пуассона.
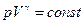 .
.
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первое начало термодинамики не определяет направления процесса. Так, не противоречит первому началу самопроизвольный переход внутренней энергии от менее нагретого к более нагретому телу. Но на практике такой переход не наблюдается. Необходимо найти критерий направленности процесса.
Равновесным называется такое состояние, в котором все параметры имеют, одинаковые значения во всей системе.
Процесс называется обратимым, если система может вернуться в первоначальное состояние, пройдя в обратном порядке через все промежуточные состояния, причем после окончаний обратного процесса не осталось бы никаких изменений в окружающей среде (процесс обратим, даже если обратный ему процесс не осуществлен, а только возможен). На p-V диаграмме изображаются только равновесные состояния и, следовательно, равновесные процессы.
Реальные процессы связаны с необратимыми потерями. Поэтому тепловая машина будет тем выгоднее, чем ближе к обратимому ее рабочий цикл. Надо найти меру необратимости процесса в адиабатно изолированной системе (система с теплоизолирующими стенками).
Рассмотрим идеальный газ, находящийся в определенном состоянии. Его молекулы в данный момент времени могут иметь какие-то координаты и скорости. Разобьем значения составляющих скоростей и координат молекул на достаточно большое число равных частей. Считаем равновероятными события, состоящие в нахождении данной молекулы в том или другом интервале объема. Так же равновероятны события, состоящие в том, что скорость выделенной молекулы принадлежит тому или иному интервалу скоростей. Таким образом, равновероятно нахождение данной молекулы в той или другой ячейке фазового пространства.
Назовем микросостоянием системы, в нашем случае – идеального газа, определенное распределение молекул по фазовым ячейкам. Такие распределения равновероятны и их число определяется количеством молекул системы. Но среди этих распределений существуют такие, которые отличаются друг от друга только номерами молекул, т. е. при переходе от одного такого распределения к другому в каждой ячейке число молекул не меняется. Каждое макросостояние системы осуществляется совокупностью таких микросостояний.
Число микросостояний, которыми осуществляется данное макросостояние, называется статистическим весом Р или термодинамической вероятностью этого макросостояния. Статистический вес является функцией состояния. Чем больше статистический вес данного состояния, тем больше вероятность встретить систему в этом состоянии.
Термодинамические системы состоят из статистически большого числа частиц.
Изолированная система переходит из одного состояния в другое, только если статистический вес не убывает.
 Обратимый процесс возможен в такой системе между состояниями с одинаковыми статистическими весами (рис.). Действительно, пусть
Обратимый процесс возможен в такой системе между состояниями с одинаковыми статистическими весами (рис.). Действительно, пусть  . Тогда процесс 1®2 осуществится самопроизвольно, но обратный ему процесс мог бы привести систему к состоянию 1 только с изменениями в окружающей среде, т. е. процесс 1®2 необратим. Обратное предположение
. Тогда процесс 1®2 осуществится самопроизвольно, но обратный ему процесс мог бы привести систему к состоянию 1 только с изменениями в окружающей среде, т. е. процесс 1®2 необратим. Обратное предположение 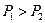 приводит к невозможности самопроизвольного процесса 1®2. Следовательно, остается одна возможность
приводит к невозможности самопроизвольного процесса 1®2. Следовательно, остается одна возможность  .
.
Таким образом, критерием необратимости процесса в изолированной системе является изменение статистического веса. Необратимый процесс в такой системе идет лишь с увеличением статистического веса; обратный ему процесс в системе с большим числом частиц настолько маловероятен, что практически не идет. Следовательно, в изолированной системе

(знак равенства относится к обратимым процессам).
Можно показать, что если система состоит из нескольких независимых частей, ее статистический вес  , где Pi – статистический вес i части.
, где Pi – статистический вес i части.
Рассмотрим систему, состоящую из одного моля идеального газа. Статистический вес, в расчете на одну молекулу, пропорционален объему сосуда:  , где С зависит от Т. При определенной температуре статистический вес моля идеального газа
, где С зависит от Т. При определенной температуре статистический вес моля идеального газа  . По этой формуле рассчитать статистический вес трудно даже для идеального газа. Введем по формуле Больцмана новую функцию состояния, называемую энтропией:
. По этой формуле рассчитать статистический вес трудно даже для идеального газа. Введем по формуле Больцмана новую функцию состояния, называемую энтропией:
 ,
,
где k – постоянная Больцмана. По этой формуле энтропия одного моля идеального газа
 .
.
Таким образом, энтропия вычисляется с точностью до некоторой постоянной S 0, но обычно нас интересует не абсолютное значение, а изменение энтропии какого-либо процесса:
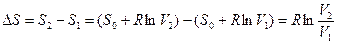 .
.
Работа изотермического расширения одного моля идеального газа равна
 .
.
Сопоставив эту формулу с предыдущим выражением, получим формулу Клаузиуса для изменения энтропии в изотермическом процессе:
 .
.
Можно показать, что эта формула справедлива для любого термодинамического тела, если D Q – количество теплоты, полученное телом в обратимом изотермическом процессе. Статистический расчет, выходящий за рамки данного «Руководства», показывает, что изменение статистического веса, а следовательно, и энтропии для обратимого адиабатного процесса равно нулю (т. е. статистический вес и энтропия в таком процессе остаются постоянными; адиабатический процесс называют иногда изоэнтропическим). Любой обратимый процесс можно разбить сколь угодно точно на достаточно большое число малых изотермических и адиабатических элементов (рис. 10). Этот ступенчатый процесс 1–2 совпадает с данным обратимым процессом в пределе при бесконечно большом числе элементов (и бесконечно малом каждом элементе). Изменение энтропии при изотермическом процессе по формуле Клаузиуса равно
 .
.
Изменение энтропии при адиабатическом процессе равно нулю. Таким образом, изменение энтропии при обратимом конечном процессе 1®2.
 .
.
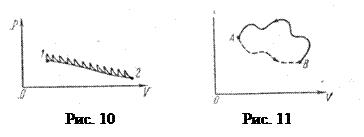 |
Используя данное выражение можно рассчитать изменение энтропии любого обратимого процесса, происходящего с каким-либо термодинамическим телом. Если процесс, происходящий с таким телом, необратим, но начальное и конечное состояния равновесны, то можно рассчитать изменение энтропии необратимого процесса А - В. На рис.11 пунктиром обозначен необратимый процесс, в котором энтропия тела изменилась на
 . Сплошная линия изображает какой-либо обратимый процесс В - А, в котором энтропия тела изменилась на
. Сплошная линия изображает какой-либо обратимый процесс В - А, в котором энтропия тела изменилась на  . Но изменение энтропии за цикл А - В - А равно нулю (тело вернулось в первоначальное равновесное состояние А, а энтропия – функция состояния):
. Но изменение энтропии за цикл А - В - А равно нулю (тело вернулось в первоначальное равновесное состояние А, а энтропия – функция состояния):
 . Отсюда
. Отсюда  .
.
Таким образом, можно рассчитать изменение энтропии и необратимого процесса, происходящего с телом, если начало и конец этого процесса равновесны (и d Q получено в соответствующем обратимом процессе). Изменение энтропии всей изолированной системы равно нулю, если все процессы, протекающие в такой системе, обратимы. В самом деле, как было доказано, в результате обратимых процессов не меняется статистический вес, который связан с энтропией формулой Больцмана. Если хоть один процесс, протекающий в изолированной системе, необратим, статистический вес, а следовательно, и энтропия такой системы возрастает. Поэтому для изолированной системы справедливо неравенство Клаузиуса:
 .
.
Неравенство Клаузиуса является по существу вторым началом термодинамики: энтропия изолированной системы не убывает. Энтропия изолированной системы постоянна, если в системе протекают только обратимые процессы. В реальной изолированной системе процессы необратимы и энтропия возрастает.
Реальные процессы, таким образом, протекают в определенном направлении.
Но сформулированное так категорически, второе начало термодинамики не является абсолютным, а имеет статистический смысл: энтропия изолированной системы может и уменьшаться, но вероятность этого процесса тем меньше, чем больше число частиц в системе, и для системы, состоящей из большого числа частиц, ничтожно мала. Каждый наблюдал так называемый «танец» пылинок в солнечном луче. Рассмотрим одну поднимающуюся пылинку, образующую с окружающими молекулами воздуха (и с Землей) практически изолированную систему. Пылинка находится в термодинамическом равновесии с воздухом. Потенциальная (механическая) энергия пылинки увеличивается за счет внутренней энергии воздуха, т. е. энтропия системы уменьшается. То, что это событие наблюдается, показывает, что его вероятность не бесконечно мала. Но ожидать, что под действием беспорядочно движущихся молекул поднимется, например, это пособие, не стоит, ибо вероятность этого события ничтожна.
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ВЯЗКОЙ СРЕДЕ
При относительном движении твердого тела и вязкой среды на тело действует сила сопротивления, которая по закону Ньютона равна (при малых скоростях)
 ,
,
где r – коэффициент, численно равный силе сопротивления при единичной скорости;  – скорость относительного движения. Знак минус показывает, что сила сопротивления направлена в сторону противоположную направлению скорости.
– скорость относительного движения. Знак минус показывает, что сила сопротивления направлена в сторону противоположную направлению скорости.
При движении в вязкой среде на тело действует сила внутреннего трения.
 .
.
Итак, на тело действуют две силы: сила сопротивления, определяемая скоростью движения, и сила вязкого трения, определяемая градиентом скорости.
Так как сила, действующая на тело, движущееся в жидкости (или газе), зависит от относительной скорости жидкости и тела, можно перейти к рассмотрению обтекания жидкостью неподвижного тела.
Пока скорость течения мала (ламинарное движение), градиент скорости тоже мал и в основном на тело действует сила сопротивления.
С ростом скорости увеличивается градиент скорости и сила внутреннего трения. Если течение становится турбулентным (образуются вихри), то сила сопротивления увеличивается нелинейно (пропорционально высшим степеням скорости). В турбулентном течении коэффициент силы сопротивления начинает зависеть от скорости. Но, по-прежнему, сила сопротивления больше силы внутреннего трения.
Коэффициент сил сопротивления при ламинарном движении жидкости зависит от формы тела, его размеров и коэффициента вязкости среды. Стокс рассчитал этот коэффициент для шарика малого радиуса а, медленно равномерно движущегося в безграничной среде с коэффициентом вязкости h:
 .
.
Из соотношений получаем (без учета знака) выражение для силы сопротивления
 .
.
Эта формула может быть использована для экспериментального определения коэффициента вязкости.
Date: 2015-11-15; view: 523; Нарушение авторских прав