Жалпы ұғымдар мен анықтамалар

Анықтама 1. Мына түрдегі

(1)

системаны жай дифференциалдық теңдеулер системасы деп атайды.

Мұнда функциялары белгілі, ал белгісіз функциялар. сандарының ең үлкенін (1) системаның реті деп атайды. Мысалға бірінші ретті системаға тек қана х -айнымалысы функциялары және олардың бірінші ретті туындылары: кіреді, ал екінші ретті системаға тағы да екінші ретті туындылары кіруге тиіс.

Анықтама 2. Белгілі бір I аралықта анықталған 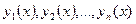функцияларының системаға кіретін туындыларының барлығы бар болса, және көрсетілген функциялар жиынтығы (1) системаны қанағаттандыратын болса, онда осы функциялар жиынтығын (1) системаның I аралығындағы шешімі деп атайды.

Өте көп физикалық процесстер дифференциалдық теңдеулер системасымен сипаттталатыны белгілі. Дифференциалдық теңдеулер системасын қарапайым түрде жазу үшін векторлық белгілеулерді пайдаланамыз.

Мысалға, функциялар жиынтығын төмендегідей белгілейміз:

Мұнда -скаляр аргумент х -тің векторлық функциясы деп аталады.

Векторлық функцияның туындылары:

түрінде анықталатыны белгілі.

(2)

түрдегі бірінші ретті дифференциалдық теңдеулер системасын векторлық түрде

(23)

жазылуын аламыз.

Дифференциалдық теңдеулер системасының ішінде (3) түрдегі системаның орны ерекше. Өйткені (1) түрдегі система әрқашанда қосымша айнымалылар енгізу арқылы дифференциалдық теңдеудің толық курстарынан табуға болады) (3) түрдегі системаға келтіріледі. Әрине, бұл жағдайда системаның теңдеулер саны көбейетіні анық.

Егер (2) системада теңдеулер саны белгісіз функциялар санына тең болса (n =l) және системаны құрайтын теңдеулер туындыларға қатысты шешілсе, онда (2) системаны мына түрде

(4)

немесе векторлық түрде

()

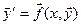жазуға болады.

Анықтама 3. (4) немесе () түрдегі дифференциалдық теңдеулер системасын қалыпты жай дифференциалдық теңдеулер системасы дейді. Кейбір жағдайда белгісіз функциялар санын қалыпты системаның реті деп те атайды.

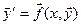Бұдан былайғы жерде дифференциалдық теңдеулердің қалыпты системасын қарастырамыз. Оны векторлық түрде, яғни () түрде демек түрде жазамыз. Мұнда

Көріп отырғанымыздай жоғары индекстер вектордың координаталарының нөмерлерін көрсететін болады. 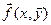функциясы облысында анықталған деп есептейміз. Мұнда өлшемді 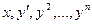айнымалыларының евклид кеңістігі. Егер мына шарттар:

1). векторлық функциясы I аралығында үзілісссіз дифференциалданатын болса

2).

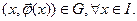
3). орындалатын болса, онда 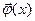функциясы () системасының шешімі деп аталады.

Коши есебінің бар және жалғыз болуы туралы теорема

Айталық,

(5)

дифференциалдық теңдеулердің қалыпты системасы берілсін.

(6)

шартын қанағаттандыратындай (5) системаның шешімін табуды (5) система үшін тұжырымдалған Коши есебі дейді.

(6) шартты бастапқы шарт деп атайды. шамаларын бастапқы берілімдер дейді. Бұдан былай (5)-(6) Коши есебі деп айтатын боламыз.

(5)- (6) Коши есебінің

(7)

интегралдық теңдеуге эквивалентті болатынын еске салайық.

(Бұл тұжырым скаляр функция үшін дәлелденген).

Теорема 1 (Пикар).

Егер функциясы R: тұйық цилиндрінде үзіліссіз функция болса және осы R цилиндрінде Липшиц шарты, демек 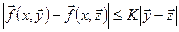орындалса, онда қандайда бір нүктесінің төңірегі да (2.5)–(2.6) Коши есебінің жалғыз ғана шешімі бар болады.

Мұнда 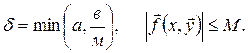(ескерту: ; векторының модулін анықтайды).

Теореманың дәлелдеуі f(x,y) скаляр функция болғандағы Пикар теоремасының дәлелдеу жолы арқылы іске асады. Ондағы y(x) скаляр функциясын -векторлық функциямен ауыстырса болғаны.

Date: 2015-11-15; view: 959; Нарушение авторских прав