Эйлер әдісі

Эйлер әдісі бойынша (16) системаның шешімін

(17)

түрінде іздейміз, мұнда

(18)

-белгісіз сан. (17) вектор функцияның туындысы

(19)

(18) және (19) өрнектерді (16) теңдікке апарып қоямыз:

немесе (20)

мұнда Е-бірлік матрица. (20) системаны координаттық формада былай да жазуға болады:

(21)

(21) алгебралық сызықтық біртектес системаның нөлден өзгеше шешімдері бар болу үшін, оның негізгі анықтауышы

нөлге тең болуы керек, демек

(22)

(22) теңдеу сипаттаушы теңдеу деп аталады. Ал оның сол жағы -ға қарағанда көпмүшелік болады. Оны сипаттаушы көпмүшелік дейді. -ның мәндері (22) сипаттаушы теңдеудің түбірі болғанда (21) системаның нөлден өзгеше шешімдерін табуға болады. Мұндай шешімдерді А-матрицасының меншікті векторлары, ал (22) теңдеудің түбірлерін А-матрицасының меншікті мәндері деп атайды. Әрбір меншікті векторға бір меншікті мән сәйкес келеді, керісінше бір меншікті мәнге бірнеше меншікті векторлар сәйкес келуі мүмкін.

Егер (22) теңдеудің түбірлері әртүрлі болса, онда осы түбірлерге сәйкес келетін (21) системаның шешімдерін табамыз.

Енді векторын (18) теңдікке апарып қойсақ, (16) сызықтық біртектес дифференциалдық системаның сызықты тәуелсіз n шешімін аламыз.

немесе ,

(16) дифференциалдық теңдеулер системасының жалпы шешімі

немесе

түрінде анықталады. -еркін тұрақтылар.

Біз жоғарыда дербес жағдайды ғана қарастырдық. Системаның шешімін іздеуде сипаттаушы теңдеудің түбірлері әртүрлі болсын деп жорыдық. Егер сипаттаушы теңдеудің түбірлерінің (А-матрицасының меншікті мәндері) ішінде еселі түбірлер болған жалпы жағдайда, берілген системаның шешімін іздеу үшін төмендегі теорема қолданылады.

Теорема 7. Айталық, А-матрицасының m -әртүрлі меншікті мәндері 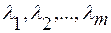және сызықты тәуелсіз векторлары болсын. Осы жағдайда (16) біртектес системаның шешімі мына түрде анықталады:

Мұнда вектор-функциялар.

Бұл вектор-функциялардың координаттары дәрежесі ()– ден аспайтын көпмүшеліктер. Мұнда - меншікті мәннің еселігі, ал -ге сәйкес келетін матрицаның сызықты тәуелсіз векторларының саны.

Мысал-1. системасының жалпы шешімін тап.

А-матрицасын жазамыз: , сипаттаушы теңдеуді шешеміз

А- матрицасының меншікті векторын табу үшін

системасын құрамыз.

a) да системадан осыдан

Ал

b) да системадан осыдан

Ал егер болса, онда 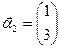берілген системаның фундаментальды шешімдер системасы мына түрде болады:

жалпы шешімі немесе координаттық түрде

болады.

Мысал-2. Системасының жалпы шешімін тап. (Жоғарғы индекстер функцияның нөмірін көрсететінін ескертеміз)

Сипаттаушы теңдеуді құрамыз:

Меншікті векторды анықтаймыз.

болғанда, төмендегі системаны аламыз:

осыдан , егер деп алсақ, онда

- меншікті векторды табамыз

осыдан

жалпы шешім:

координаттық формада:

түрінде болады

Date: 2015-11-15; view: 2626; Нарушение авторских прав