
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ДӘРІС 13
|
|
Дәріс сабақтың құрылымы:
1 Жоғарғы ретті сызықтық дифференциалдық теңдеулер
2 Сызықтық біртектес теңдеулер
3 Сызықтық дифференциалдық оператор
4 Сызықтық тәуелді және сызықтық тәуелсіз функциялар жүйесі
5 Вронский анықтауышы
6 Сызықтық біртектес дифференциялдық теңдеудің жалпы шешімінің құрылымы. Лиувилль формуласы
7 Тұрақты коэффициентті сызықтық біртектес дифференциалдық теңдеулер
Дәріс сабақтың мазмұны:
 (1)
(1)
түріндегі теңдеуді n ретті сызықтық дифференциалдық теңдеу деп атайды.
Мұнда 
 ,
,  функциялары белгілі бір интервал
функциялары белгілі бір интервал  -да берілген функциялар.
-да берілген функциялар.
Егер g(x)  0 болса, онда (1) теңдеуді сызықтық біртектес теңдеу дейді. Ал
0 болса, онда (1) теңдеуді сызықтық біртектес теңдеу дейді. Ал
Ал  , онда сызықтық біртектес емес теңдеу болады.
, онда сызықтық біртектес емес теңдеу болады.
Айталық,
 сызықтық біртектес теңдеуі берілсін.
сызықтық біртектес теңдеуі берілсін.
Егер белгілі бір интервалда  болса, онда берілген теңдеудің барлық мүшелерін
болса, онда берілген теңдеудің барлық мүшелерін  -ке бөліп төмендегі теңдеуді аламыз
-ке бөліп төмендегі теңдеуді аламыз
 (2)
(2)
Еске сала кетейік. Егер (2) теңдеудегі 
 ,
,
f(x) белгілі бір интервалда үзіліссіз болса, онда (1) теңдеу үшін тұжырымдалған Коши есебінің жалғыз ғана шешімінің бар болатынын өткен тарауда көрсеткен болатынбыз.
Айталық Е және F функциялар жиыны болсын. Егер әрбір  функциясына белгілі бір заңдылық бойынша бір ғана
функциясына белгілі бір заңдылық бойынша бір ғана  функциясы сәйкес қойылса, онда мәндері F жиынында жататын, Е жиынында анықталған (берілген) оператор берілді дейді.
функциясы сәйкес қойылса, онда мәндері F жиынында жататын, Е жиынында анықталған (берілген) оператор берілді дейді.
Оны былай белгілейді А:  , немесе f=Ay.
, немесе f=Ay.
Егер Е сызықтық кеңістік болса және мына теңдіктер
1)  ,
, 
2)  ,
, 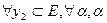 -сан
-сан
орындалса онда А сызықтық оператор деп аталады. (2) теңдеудің сол жағын L [ y ] арқылы белгілейік:
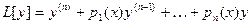 L-сызықтық оператор болады.
L-сызықтық оператор болады.
Шынында да,

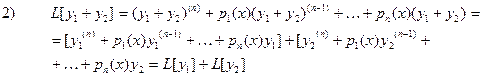
осының салдары ретінде

теңдігін аламыз мұнда  - тұрақтылар
- тұрақтылар  - операторын бұдан былай сызықтық дифференциалдық оператор деп атайтын боламыз.
- операторын бұдан былай сызықтық дифференциалдық оператор деп атайтын боламыз.
Ал (4.2) теңдеуді қысқа түрде  (2/)
(2/)
Сызықтық біртектес теңдеудің кейбір қасиеттерін көрсетеміз.
Теорема 1. Егер  функциялары
функциялары  сызықтық біртектес теңдеудің шешімдері болса онда олардың сызықтық канбинациясы
сызықтық біртектес теңдеудің шешімдері болса онда олардың сызықтық канбинациясы  да
да 
 теңдеудің шешімі болады.
теңдеудің шешімі болады.
Дәлелдеуі. Шарт бойынша 
 .
.
Дәлелдеу керек  болатынын.
болатынын.  -операторы сызықтық болғандықтан
-операторы сызықтық болғандықтан  , өйткені
, өйткені  осыдан
осыдан 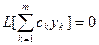 болады, демек,
болады, демек,  функциясы
функциясы  теңдеуінің шешімі.
теңдеуінің шешімі.
Теорема 2. Егер 
 функциясы коэффиценттері
функциясы коэффиценттері 
 нақты болатын
нақты болатын  сызықтық бітектес теңдеудің комплекс шешімі болса, онда оның нақты бөлігі де және жорамал бөлігі де
сызықтық бітектес теңдеудің комплекс шешімі болса, онда оның нақты бөлігі де және жорамал бөлігі де  теңдеуінің шешімі болады.
теңдеуінің шешімі болады.
Дәлелдеуі. Шарт бойынша  L- сызықтық оператор болғандықтан
L- сызықтық оператор болғандықтан  . Ал комплекс сан нольге тең болу үшін оның нақты және жорамал бөлігі нольге тең болуы тиіс. Сондықтан
. Ал комплекс сан нольге тең болу үшін оның нақты және жорамал бөлігі нольге тең болуы тиіс. Сондықтан  және
және  . Демек
. Демек  және
және  функциялары да (2/) теңдеуінің шешімі екен.
функциялары да (2/) теңдеуінің шешімі екен.
Айталық  функциялар системасы (а,в) интервалында берілсін.
функциялар системасы (а,в) интервалында берілсін.
Анықтама 1. Егер барлығы бірдей нольге тең емес 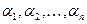
сандары табылып,
 (3)
(3)
тепе-теңдігі орындалса, онда  функциялар системасы
функциялар системасы  интервалында сызықты тәуелді дейді.
интервалында сызықты тәуелді дейді.
Егер (3) тепе-теңдік тек қана  болғанда орындалса онда
болғанда орындалса онда  функциялары
функциялары  интервалында сызықты тәуелсіз деп аталады.
интервалында сызықты тәуелсіз деп аталады.
Бірнеше мысалдар келтірейік.
1. Айталық,  бұл функциялар кез келген
бұл функциялар кез келген
интервалда сызықты тәуелді.
Шынында да  болғанда
болғанда  көреміз.
көреміз.
2. Енді  ,
, 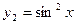 ,
,  ,
,  ,
,  ,
, 
функцияларын қарайық. Бұл функциялар системасы да сызықты
тәуелді болады. Егер 
 деп алсақ, онда
деп алсақ, онда  белгілі бір
белгілі бір  интервалында, бірақ
интервалында, бірақ  кез келген болмауы мүмкін.
кез келген болмауы мүмкін.
Осы мысалдан мынаны байқаймыз: Егер функциялар системасының бір бөлігі сызықты тәуелді болса, онда барлық система да сызықты тәуелді болады.
Екі функцияның сызықты тәуелділігі оның біреуі екіншісін бір нольге тең емес санға көбейткеннен шығатынын көрсетеді, яғни 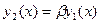 ,
,  . Сондай-ақ,
. Сондай-ақ,  функциялар системасы (a,b) аралықта сызықты тәуелді болса, онда оның ең кемінде біреуін қалғандарының сызықтық комбинациясы түрінде өрнектеуге болады.
функциялар системасы (a,b) аралықта сызықты тәуелді болса, онда оның ең кемінде біреуін қалғандарының сызықтық комбинациясы түрінде өрнектеуге болады.
Шынында да, сызықты тәуелді болғандықтан  ,
,  . Анықтық үшін
. Анықтық үшін  болсын. Онда
болсын. Онда  , мұнда
, мұнда 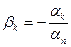 .
.
3.  функциялар системасы сызықты тәуелсіз болады.Шынында да, айталық
функциялар системасы сызықты тәуелсіз болады.Шынында да, айталық  барлығы бірдей нольге тең емес сандар болса, онда
барлығы бірдей нольге тең емес сандар болса, онда

теңдігі (n- 1) дәрежелі теңдеу болады. Ал оның түбірлерінің саны (n- 1)-ден арта алмайтыны белгілі. Сондықтан, 
өрнегі кез келген интервалдың барлық нүктесінде нольге айнала алмайды. Тепе-теңдік 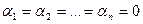 болғанда ғана орындалады. Ендеше,
болғанда ғана орындалады. Ендеше,  функциялар системасы анықтама бойынша сызықты тәуелсіз. Осы дәлелдеулерден кейбір функциялар системасының сызықты тәуелділігін немесе сызықты тәуелсіздігін тағайындауға мүмкіндік беретіндей белгіллерді қарастыру қажеттігі туғанын байқаймыз. Енді осы мәселеге кірісейік.
функциялар системасы анықтама бойынша сызықты тәуелсіз. Осы дәлелдеулерден кейбір функциялар системасының сызықты тәуелділігін немесе сызықты тәуелсіздігін тағайындауға мүмкіндік беретіндей белгіллерді қарастыру қажеттігі туғанын байқаймыз. Енді осы мәселеге кірісейік.
Егер  функциялар системасы (n -1) рет дифференциалданатын болса, онда олардан төмендегі n ретті анықтауышты құруға болады:
функциялар системасы (n -1) рет дифференциалданатын болса, онда олардан төмендегі n ретті анықтауышты құруға болады:

Бұл анықтауыш x айнымалысының функциясы болатыны белгілі, демек  . Енгізілген анықтауышты Вронский анықтауышы немесе вронскиан деп атайтын боламыз (И.Вронский поляк математигі).
. Енгізілген анықтауышты Вронский анықтауышы немесе вронскиан деп атайтын боламыз (И.Вронский поляк математигі).
Теорема 3. (сызықты тәуелділіктің қажетті шарты)
Егер  функциялары (a,b) аралығында (n- 1) рет дифференциалданатын сызықты тәуелді функциялары болса, онда осы функциялардан құрылған Вронский анықтауышы нольге тепе-тең болады, яғни,
функциялары (a,b) аралығында (n- 1) рет дифференциалданатын сызықты тәуелді функциялары болса, онда осы функциялардан құрылған Вронский анықтауышы нольге тепе-тең болады, яғни,  ,
,  .
.
Дәлелдеуі: Көрнекілік үшін n =3 жағдайын дәлелдейміз. Айталық  функциялары (a,b)-да сызықты тәуелді болсын. Онда барлығы бірдей нольге тең емес
функциялары (a,b)-да сызықты тәуелді болсын. Онда барлығы бірдей нольге тең емес  сандары табылып
сандары табылып
 ,
,  болады. Анықтық үшін,
болады. Анықтық үшін, 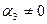 . Онда
. Онда  , мұнда
, мұнда  ,
,  .
.
Вронский анықтауышын құрамыз.
 ;
;
 ,
,  , себебі соңғы екі қосылғыш анықтауыштардың екі бағанының элементтері пропорционал. Сондықтан, анықтауыштың белгілі қасиеті бойынша нольге тең болады. Теорема толығымен дәлелденді.
, себебі соңғы екі қосылғыш анықтауыштардың екі бағанының элементтері пропорционал. Сондықтан, анықтауыштың белгілі қасиеті бойынша нольге тең болады. Теорема толығымен дәлелденді.
Керісінше пайымдау арқылы төмендегі теореманы өте жеңіл дәлелдеуге болады.
Теорема 4. Егер берілген n функция үшін құрылған Вронский анықтауышы кейбір (a,b) интервалында тепе-тең нөльге тең болмаса, онда осы интервалда берілген функциялар сызықты тәуелсіз болады.
Теорема 5. (шешімдердің сызықты тәуелсіздігінің қажетті шарты)
(a,b) интервалында сызықты тәуелсіз функциялар  , коэффициенттері
, коэффициенттері  (a,b) интервалында үзіліссіз болатын
(a,b) интервалында үзіліссіз болатын
 (4)
(4)
сызықтық біртектес дифференциалдық теңдеудің шешімдері болса, онда осы функциялар системасының Вронский анықтауышы

(a,b) интервалының ешбір нүктесінде нольге айнала алмайды.
Дәлелдеуі. Оңайлық үшін n =3 болсын. Айталық, 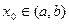 нүктесінде
нүктесінде 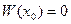 деп кері жорыйық. Төменде
деп кері жорыйық. Төменде  қарағанда сызықтық біртектес алгебралық системаны құрайық:
қарағанда сызықтық біртектес алгебралық системаны құрайық:
 (5)
(5)
Жоруымыз бойынша (5) системасының анықтауышы 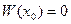 . Сондықтан (5) системаның ноль емес шешімі бар болады. Оны
. Сондықтан (5) системаның ноль емес шешімі бар болады. Оны  арқылы белгілейік. Мұнда осы үш санның ең кемінде біреуі нольден өзгеше. Енді мына
арқылы белгілейік. Мұнда осы үш санның ең кемінде біреуі нольден өзгеше. Енді мына
 (6)
(6)
функцияны қарастырамыз. Бұл функция (4) теңдеудің шешімдерінің сызықтық комбинациясы болғандықтан ол берілген біртектес теңдеудің шешімі болып табылады және (6) шешім (5) теңдеулердің негізінде нольдік бастапқы шарттарды қанағаттандырады.
Яғни, 


Мұндай бастапқы шартты, көрініп тұрғандай, (4.4) теңдеудің нольдік шешімі  де қанағаттандырады. Онда шешімнің жалғыз болуы туралы теорема бойынша
де қанағаттандырады. Онда шешімнің жалғыз болуы туралы теорема бойынша
 ,
, 
болады, оның үстіне  -дің
-дің  кемінде біреуі нольден өзгеше. Ендеше
кемінде біреуі нольден өзгеше. Ендеше  функциялары (a,b) интервалында сызықты тәуелді. Бұл қорытынды теореманың шартына қайшы. Олай болса біздің жоруымыз қате, теореманың тұжырымы дұрыс деген сөз. Демек,
функциялары (a,b) интервалында сызықты тәуелді. Бұл қорытынды теореманың шартына қайшы. Олай болса біздің жоруымыз қате, теореманың тұжырымы дұрыс деген сөз. Демек,  Теорема 3 пен Теорема 4 ден салдар ретінде төмендегі теорема шығады.
Теорема 3 пен Теорема 4 ден салдар ретінде төмендегі теорема шығады.
Теорема 6. (a,b) аралығында коэффициенттері үзіліссіз болатын (4) сызықтық біртектес дифференциалдық теңдеудің дербес шешімдері  , (a,b) интервалында сызықты тәуелсіз болу үшін шешімдердің системасының вронскианы нольден өзгеше болуы қажетті және жеткілікті.
, (a,b) интервалында сызықты тәуелсіз болу үшін шешімдердің системасының вронскианы нольден өзгеше болуы қажетті және жеткілікті.
Дәлелдеуі. Қажеттілігі теорема 4 ден шығады. Жеткіліктілігі теорема 3 ден шығады. Себебі  функциялары сызықты тәуелді болса, онда
функциялары сызықты тәуелді болса, онда  . Сондықтан
. Сондықтан  -са
-са  функциялары сызықты тәуелді бола алмайды. Демек, олар сызықты тәуелсіз.
функциялары сызықты тәуелді бола алмайды. Демек, олар сызықты тәуелсіз.
Теорема 7. D: a<x<b,  , k= 0,1 ,…, (n- 1) облысында коэффициенттері
, k= 0,1 ,…, (n- 1) облысында коэффициенттері  k =0,1,…, n [a,b] сегментінде үзіліссіз болатын
k =0,1,…, n [a,b] сегментінде үзіліссіз болатын
 (7)
(7)
сызықтық біртектес дифференциалдық теңдеудің жалпы шешімі мына түрде
 (8)
(8)
анықталады. Мұнда  ,
,  (1) теңдеудің сызықты тәуелсіз дербес шешімдері, ал
(1) теңдеудің сызықты тәуелсіз дербес шешімдері, ал  еркін тұрақтылар.
еркін тұрақтылар.
Дәлелдеуі. (8) функция (7) теңдеудің жалпы шешімі болуы үшін екі шартты қанағаттандыруы керек: Біріншісі  параметрлерінің барлық мәндерінде (8) функция (7) теңдеудің шешімі болуы тиіс. Бұл талап орындалады. (IV-тарау, §1, Т.1 қараңыз).
параметрлерінің барлық мәндерінде (8) функция (7) теңдеудің шешімі болуы тиіс. Бұл талап орындалады. (IV-тарау, §1, Т.1 қараңыз).
(7) теңдеу үшін көрсетілген D облысында бар болу және жалғыздық теоремасының барлық шарттары орындалатыны белгілі. Екіншісі, кез келген берілген бастапқы
 ,
,  ,
,  (9)
(9)
шартты (8) функция қанағаттандыратындай  параметрлерінің мәндерінің бар болуын көрсету. Көрнекілік үшін n =3 деп аламыз. Егер
параметрлерінің мәндерінің бар болуын көрсету. Көрнекілік үшін n =3 деп аламыз. Егер  функциясы (9) бастапқы шартты қанағаттандырсын деп талап қойсақ, онда мына
функциясы (9) бастапқы шартты қанағаттандырсын деп талап қойсақ, онда мына
 (10)
(10)
сызықтық алгебралық теңдеулер системасын аламыз. Бұл системаның анықтауышы  (Вронскиан), себебі
(Вронскиан), себебі  функциялары шарт бойынша (7) теңдеудің сызықты тәуелсіз шешімдері, олай болса (4.10) теңдеулер системасы
функциялары шарт бойынша (7) теңдеудің сызықты тәуелсіз шешімдері, олай болса (4.10) теңдеулер системасы  , кез келген
, кез келген  үшін бірмәнді түрде шешіледі. Бұл (8) функция (9) бастапқы шартты қанағаттандыратындай
үшін бірмәнді түрде шешіледі. Бұл (8) функция (9) бастапқы шартты қанағаттандыратындай  параметрлерінің мәндерін таңдап алатындай мүмкіндік бар екенін көрсетеді. Демек (7) теңдеудің жалпы шешімі оның
параметрлерінің мәндерін таңдап алатындай мүмкіндік бар екенін көрсетеді. Демек (7) теңдеудің жалпы шешімі оның  сызықты тәуелсіз дербес шешімдерінің сызықтық комбинациясы болып табылады.
сызықты тәуелсіз дербес шешімдерінің сызықтық комбинациясы болып табылады.
Анықтама 2 n ретті сызықтық біртектес дифференциалдық теңдеудің кез келген n сызықты тәуелсіз шешімдерінің жиынтығын оның фундаментальды шешімдер системасы дейміз.
Теорема 8. Коэффициенттері  k= 0,1 ,…,n үзіліссіз болатын әрбір сызықтық біртектес дифференциалдық теңдеудің фундаментальды шешімдер системасы бар болады (ол тіпті ақырсыз жиын құрайды).
k= 0,1 ,…,n үзіліссіз болатын әрбір сызықтық біртектес дифференциалдық теңдеудің фундаментальды шешімдер системасы бар болады (ол тіпті ақырсыз жиын құрайды).
Мысалға коэффициенттері  k =0,1,…, n [ a,b ]-да үзіліссіз болатын
k =0,1,…, n [ a,b ]-да үзіліссіз болатын
 (11)
(11)
теңдеуін алайық.
Айталық,
 ,
,  (12)
(12)
 нүктесінде төмендегі тиісінше бастапқы шарттарды қанағаттандыратын (11) теңдеудің шешімдері болсын:
нүктесінде төмендегі тиісінше бастапқы шарттарды қанағаттандыратын (11) теңдеудің шешімдері болсын:





(4.12) шешімдердің  нүктесіндегі Вронский анықтауышы
нүктесіндегі Вронский анықтауышы
 болады.
болады.
Демек, (12) шешімдер (11) теңдеудің фундаментальды шешімдер системасын құрайды. Осыдан бастапқы берілімдерді:
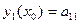 ,
,  ,
,  ,
,  сан алуан түрде алуға болатыны шығады.
сан алуан түрде алуға болатыны шығады.
Тек қана  шарты орындалсажеткілікті.
шарты орындалсажеткілікті.
Көріп отырғанымыздай, бастапқы шартты өзгерткен сайын фундаментальды шешімдер системасы да өзгеріп отырады. Ендеше олар ақырсыз жиын құрайды.
Теорема 9. Егер екі теңдеудің
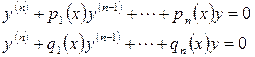
(мұнда 
 сегментінде үзіліссіз функциялар)
сегментінде үзіліссіз функциялар)
y 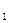 (x),y
(x),y  (x),…,y
(x),…,y  (x) –функциялары ортақ фундаментальды шешімдер системасы болса, онда бұл теңдеулер үйлеседі, демек
(x) –функциялары ортақ фундаментальды шешімдер системасы болса, онда бұл теңдеулер үйлеседі, демек  болады. Көрсетілген теореманың дәлелдемесін дифференциалдық теңдеулердің басқа толық курсынан табуға болады.
болады. Көрсетілген теореманың дәлелдемесін дифференциалдық теңдеулердің басқа толық курсынан табуға болады.
Сонымен, теорема 9 –дан шығатын қорытынды (7) түрдегі сызықтық біртектес теңдеу, оның фундаментальды шешімдер системасымен толық анықталатындығы, демек  коэффициенттерін фундаментальды шешімдер системасының көмегімен бір мәнді анықтауға болады.
коэффициенттерін фундаментальды шешімдер системасының көмегімен бір мәнді анықтауға болады.
Сол жағы анықтауыш арқылы өрнектелетін дифференциалдық теңдеуді қарастырайық:
 (4.13)
(4.13)
мұнда у(х) ізделіп отырған функция, ал y  (x),y
(x),y  (x),…,y
(x),…,y  (x) – берілген фундаментальды шешімдер системасы.
(x) – берілген фундаментальды шешімдер системасы.
y 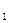 (x),y
(x),y  (x),…,y
(x),…,y  (x) функциалары (13) теңдеудің шешімдері болатынын көру қиын емес. Өйткені y(x) функциясының орнына осы функциялардың әрқайсысын қойғанда анықтауыштың екі бағанының элементтері бірдей болады. Сондықтан анықтауыш нольге айналады.
(x) функциалары (13) теңдеудің шешімдері болатынын көру қиын емес. Өйткені y(x) функциясының орнына осы функциялардың әрқайсысын қойғанда анықтауыштың екі бағанының элементтері бірдей болады. Сондықтан анықтауыш нольге айналады.
Анықтауышты соңғы бағанының элементтері бойынша жіктегенде (13) теңдеуден төмендегі теңдеуді аламыз:
W(x)y 



 (14)
(14)
Мұнда W(x)-y 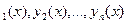 функциаларының Вронский анықтауышы. Ал
функциаларының Вронский анықтауышы. Ал

Анықтауыш W(x) 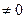 ,
,  өйткені y
өйткені y  фундаментальды шешімдер системасы. Ендеше (14) теңдеудің барлық мүшелерін W(x)- ке бөлу арқылы оны мына түрге келтіреміз:
фундаментальды шешімдер системасы. Ендеше (14) теңдеудің барлық мүшелерін W(x)- ке бөлу арқылы оны мына түрге келтіреміз:
y 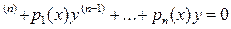
Мұнда, жекелеп алғанда, 
Егер n ретті  анықтауышының элементтері дифференциалданатын a
анықтауышының элементтері дифференциалданатын a  түріндегі функциялар болса, онда
түріндегі функциялар болса, онда  анықтауышының туындысы төмендегі формула бойынша анықталатынын дәлелдеуге болады:
анықтауышының туындысы төмендегі формула бойынша анықталатынын дәлелдеуге болады:
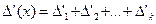
Мұнда 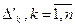
 анықтауышынан нөмірі k -ға тең болатын жолды оның туындысымен ауыстырғандағы шыққан анықтауышқа тең.
анықтауышынан нөмірі k -ға тең болатын жолды оның туындысымен ауыстырғандағы шыққан анықтауышқа тең.
Мысалға  функцияларының Вронский анықтауышы үшін мына теңдік
функцияларының Вронский анықтауышы үшін мына теңдік

орындалатынын көреміз. Осы айтылғанның негізінде


теңдігін тексеру қиын емес. Демек,
P 
Соңғы теңдеуді x бойынша x  -ден x-ке дейін интегралдау арқылы
-ден x-ке дейін интегралдау арқылы
W(x)=W( )e
)e  формуласын аламыз. Бұл формуланы Остраградский-Лиувилль формуласы деп атайды.
формуласын аламыз. Бұл формуланы Остраградский-Лиувилль формуласы деп атайды.
Шешімдері  болатынын екінші ретті сызықтық біртектес теңдеуді құр.
болатынын екінші ретті сызықтық біртектес теңдеуді құр.
Берілген функциялар сызықты тәуелсіз екендері белгілі. Жоғарыдағы айтылғандарға сәйкес іздеп отырған теңдеуіміз мына түрде болады:





Осыдан  ,
, 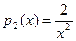
Бұл функциялар x= 0 нүктесінде үзіліске ұшырайды. Сондықтан осы функциялардың Якобианы  , x= 0 нүктесінде нөльге айналады, демек x= 0 нүктесінде сызықты тәуелсіз шешімдердің қажетті шарты орындалмайды.
, x= 0 нүктесінде нөльге айналады, демек x= 0 нүктесінде сызықты тәуелсіз шешімдердің қажетті шарты орындалмайды.
Теорема 10. Егер  (7) теңдеуінің дербес шешімі болса, онда u айнымалысын
(7) теңдеуінің дербес шешімі болса, онда u айнымалысын  (*) формуласы бойынша енгізу арқылы сызықтық біртектес теңдеудің ретін бірге кемітуге болады және шыққан теңдеу де сызықтық болады.
(*) формуласы бойынша енгізу арқылы сызықтық біртектес теңдеудің ретін бірге кемітуге болады және шыққан теңдеу де сызықтық болады.
Дәлелдеуі
 функциясының төмендегі туындыларын табамыз.
функциясының төмендегі туындыларын табамыз.
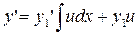

------------------------------------
 =
= 
Осы туындылардың өрнектерін (4.7) теңдеуге апарып қойып, төмендегі теңдеуді аламыз.

Шарт бойынша,  шешім. Сондықтан
шешім. Сондықтан  Онда соңғы теңдеу төмендегі түрге келеді.
Онда соңғы теңдеу төмендегі түрге келеді.

Мұнда  k =1,2,…,(n -1).
k =1,2,…,(n -1).
Теорема дәлелденді.
Мысал-1.  теңдеуінің жалпы шешімін тап.
теңдеуінің жалпы шешімін тап.
 функциясы берілген теңдеудің дербес шешімі болады. (Тексеріп көріңдер).
функциясы берілген теңдеудің дербес шешімі болады. (Тексеріп көріңдер).
Берілген теңдеудің ретін кеміту үшін 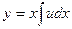 формуласы бойынша u айнымалысын енгіземіз. Осы функцияның туындыларын тауып, берілген теңдеуге апарып қоямыз:
формуласы бойынша u айнымалысын енгіземіз. Осы функцияның туындыларын тауып, берілген теңдеуге апарып қоямыз:

 ·
· 
Осыдан 

lnu +3ln|x|=0; u=  (бір шешім жеткілікті);
(бір шешім жеткілікті);
y2=x  =x·(-
=x·(-  )=-
)=- 

 ( бір шешім жеткілікті);
( бір шешім жеткілікті);
y 1 =x, y = - 
 функциялары сызықты тәуелсіз.
функциялары сызықты тәуелсіз.
 (тұрақты емес).
(тұрақты емес).
Онда берілген теңдеудің жалпы шешімі
 болады.
болады.
c 1 және c 2 еркін тұрақтылар.
Өзін-өзі тексеруге арналған сұрақтар:
1 Жоғарғы ретті сызықтық дифференциалдық теңдеулер
2 Сызықтық біртектес теңдеулер
3 Сызықтық дифференциалдық оператор
4 Сызықтық тәуелді және сызықтық тәуелсіз функциялар жүйесі
5 Вронский анықтауышы
6 Сызықтық біртектес дифференциялдық теңдеудің жалпы шешімінің құрылымы. Лиувилл формуласы
7 Тұрақты коэффициентті сызықтық біртектес дифференциалдық теңдеулер
Қолданылған әдебиеттер:
1. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.- М.: Наука, 1985
2. Қалиев С.Қ., Искакова М.Т. Дифференциалдық теңдеулер және варияциялық есептеу негіздері, Семей – 2005
3. Филлипов А.Ф. Сборник задач по обыкновенные дифференциальным уравнениям. М.: Наука, 1984
4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - Москва.: Изд-во МГУ, 1984.
5. Қадыкенов Б.М. Дифференциалдық теңдеулердің есептері мен жаттығулары Алматы: Қазақ университеті, 2002
Date: 2015-11-15; view: 2580; Нарушение авторских прав