Тұрақты коэффициентті сызықты біртектес емес дифференциалдық теңдеулер

Коэффиценттері тұрақты сан болғанда сызықтық біртектес емес дифференциалдық теңдеуді кейбірде оңай әдістермен, мысалы анықталмаған коэффиценттер әдісімен шығару мүмкін болады. Төменде біз осы әдіс туралы айтамыз.

1. (18)

теңдеуін қарастырамыз. Мұнда -нақты сандар, дәрежелі көпмүшелік, яғни

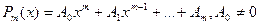
Бірінші теңдеуге сәйкес келетін біртектес теңдеудің сипаттаушы теңдеуі

(19)

немесе мұнда - сипаттаушы көпмүшелік.

а) Егер болса,

(20)

сипаттаушы теңдеудің түбірі болмайды, онда (18) теңдеудің дербес шешімі бар болады және ол m дәрежелік көпмүшелік ретінде анықталады, демек

(21)

Мұнда -анықталмаған коэффиценттер. - коэффиценттері бір мәнді түрде анықталады. Өйткені функциясының өрнегін (18) теңдеуге қойғанда, теңдеудің екі жағы бірдей дәрежелі (m дәрежелі) көпмүшелік болады. Ал екі көпмүшелік біріне-бірі тең болу үшін белгісіздің бірдей дәрежелерінің коэффиценттері тең болуға тиіс.

Осыдан анықталмаған коэфиценттерін байланыстыратын m сызықтық алгебралық теңдеулер системасын аламыз, оны шешу арқылы коэффиценттерін анықтап, (21) теңдікке апарып қойып, бірінші теңдеудің дербес шешімін табамыз.

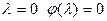б) Айталық, болсын. Жалпылық үшін, деп алайық, бірақ болсын. Бұл жағдайда теңдеудің еселі түбірі болады. Онда (18) теңдеу мына түрге келеді:

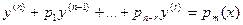(22)

а) жағдайы бойынша болуы керек, онда дәрежелі көпмүшелік болады. Және оның дәрежеден кіші дәрежелерінің коэффиценттері кез келген сандар болса да ақырғы нәтижеге әсері болмайды. Сондықтан аталған коэффиценттер нөльге тең деп есептейміз. Олай болса 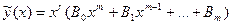түрінде іздеуге болады.

Сөйтіп, егер сипаттаушы теңдеудің 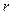еселі түбірі болса, онда (18) теңдеудің дербес шешімі коэфиценттері анықталмаған m дәрежелі көпмүшелік пен х^r -нің көбейтіндісі түрінде іздеу керек:

Мысал-4. теңдеуінің дербес шешімін тап сипаттаушы теңдеудің түбірлері жай түбір теңдеуінің оң жағы бір дәрежелі көпмүшелік, сондықтан

-ты берілген теңдеуге қойып, х-тің бірдей дәрежелерінің коэфиценттерін салыстыру арқылы 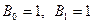болатынын көреміз. Сондықтан .

2. Енді мына түрдегі

(23)

теңдеудің шешімін іздейміз (23) теңдеудің дербес шешімі

(24)

түрінде іздейік. Мұнда функциясын

(25)

тепе-теңдігі орындалатындай етіп таңдап аламыз.

егер функцияларын тиісінше сандарына көбейтіп, бағаны бойынша қоссақ, төмендегі теңдікке келеміз.

(25) тепе-теңдігі орындалу үшін, функциясы

(26)

теңдеуінің шешімі болу керек.

Жоғарыда талқылағандай, егер демек сипаттаушы теңдеудің түбірі болмаса, онда (25) теңдеудің шешімін түрінде іздейміз. Ал (23) теңдеудің шешімі

(27)

түрінде ізделінеді.

Егер саны сипаттаушы теңдеудің r еселі түбірі болса, яғни 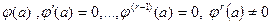онда (25) теңдеудің шешімі түрінде ізделіп, ал (23) теңдеудің шешімін

(28)

түрінде іздеуге тура келер еді. Мұнда, бұрында айтқандай m дәрежелі, коэффиценттері анықталмаған көпмүшелік,

Мысал-5. теңдеуінің дербес шешімінің түрін жаз (көрсет). 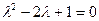сипаттаушы теңдеуінің түбірлері , демек m= 1.

Бірге тең болатын а саны сипаттаушы теңдеудің теңдеудің екі еселі (r =2) түбірі. Сондықтан дербес шешімнің түрі төмендегідей болады.

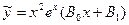
3. Жоғарыдағы келтірілген пайымдаулар а саны комплекс сан болғанда да әділ болады.

Тағы да

(29)

теңдеуін қарастырайық. Мұнда

(30)

,

формулаларын (Эйлер формулалары) пайдаланып f`(x) функциясының оң жағын төмендегі түрге келтіруге болады:

(31)

Мұнда M(x) және N(x) дәрежелері m және s санының ең үлкеніне тең болатын комплекс мәнді көпмүшеліктер.

Енді (31) формуланың оң жағындағы қосылғыштардың әрқайсысына жоғарыдағы ережені қолданып (29) теңдеудің дербес шешімінің түрін анықтауға болады. Демек, егер теңдеуінің түбірі болмаса, онда (29) теңдеудің дербес шешімін (31) түрде іздейміз. Ал егер 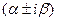сипаттаушы теңдеудің r еселі түбірі болса, онда (29) теңдеудің дербес шешімі (31) өрнек пен -нің көбейтіндісі түрінде ізделінеді.

Осы ереже f(x) функциясының алғашқы (берілген) өрнегі үшін былай тұжырымдалады:

егер сипаттаушы теңдеудің түбірі болмаса, онда (29) теңдеудің дербес шешімі түрінде ізделінетін болады. Мұнда, U(x) және V(x) тағы да дәрежелері k=max(m,s) –ге тең болатын коэффиценттері анықталмаған көпмүшеліктер.

Ал егер , сипаттаушы теңдеудің r еселі түбірі болса, онда (29) теңдеудің дербес шешімі мына түрде ізделінетін болады. Мұнда, және тағы да дәрежелері k=max(m,s) –ке тең болатын коэффиценттері анықталмаған көпмүшеліктер.

Белгісіз коэффиценттер жоғарыда көрсетілгендей анықталмаған коэффиценттер әдісі бойынша табылады.

Мысал-6. теңдеуінің дербес шешімін тап.

сипаттаушы теңдеуінің түбірлері . Біздің жағдайымызда =0, =1, сондықтан . Бұл сан сипаттаушы теңдеудің түбірі емес;

Демек, дербес шешім мына түрде .

функциясын берілген теңдеуге қойып, А =0, В = екенін табамыз.

= sin x.

Өзін-өзі тексеруге арналған сұрақтар:

1 Сызықтық біртектес емес дифференциалдық теңдеулер

2 Жалпы шешім құрылымы

3 Дербес шешім табу үшін Лагранж әдісі

4 Тұрақты коэффициентті сызықтық біртектес емес дифференциалдық теңдеулер

Қолданылған әдебиеттер:

1. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.- М.: Наука, 1985

2. Қалиев С.Қ., Искакова М.Т. Дифференциалдық теңдеулер және варияциялық есептеу негіздері, Семей – 2005

3. Филлипов А.Ф. Сборник задач по обыкновенные дифференциальным уравнениям. М.: Наука, 1984

4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - Москва.: Изд-во МГУ, 1984.

5. Қадыкенов Б.М. Дифференциалдық теңдеулердің есептері мен жаттығулары Алматы: Қазақ университеті, 2002

Date: 2015-11-15; view: 1705; Нарушение авторских прав