Мысалдар

1. 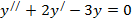теңдеуін шешу керек.

Шешуі. Берілген теңдеудің характеристикалық теңдеуі

.

Оның түбірлері , , яғни әр түрлі нақты сандар. Сонда берілген теңдеудің жалпы шешімі (4) формула бойынша

болады.

2. 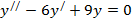теңдеуін шешу керек.

Шешуі. Берілген теңдеудің характеристикалық теңдеуі

немесе , бұдан , яғни характеристикалық теңдеудің түбірлері өзара тең нақты сандар. Сонда берілген дифференциалдық теңдеудің жалпы шешімі

.

3. теңдеуін шешу керек.

Шешуі. Теңдеудің характеристикалық теңдеуі

ал оның түбірлері

, ,

яғни түбірлері , болатын комплекс сандар. Сонда жалпы шешім:

.

n ретті біртектес емес сызықтық теңдеуді қарастырамыз.

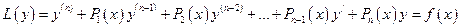(1)

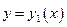функциясы (1) теңдеудің дербес шешімі болсын, яғни (2)

(3) болсын, мұндағы z – х-ке тәуелді белгісіз функция. Сонда (1) теңдеу мына түрде болады:

немесе

(2) (4) болады.

Бұл сол жағы (1) теңдеудегідей болатын біртектес теңдеу. (4) теңдеу (1) теңдеуге сәйкес біртектес теңдеу деп аталады.

() функциялары (4) теңдеудің шешімдерінің фундаментальды жүйесі болсын. Сонда бұл теңдеудің барлық шешімдері оның

(5)

жалпы шешімінде қамтылады. z-тің осы мәнін (3) теңдеуге қойсақ, (6) аламыз.

Бұл формула (1) біртектес емес теңдеудің барлық шешімдерін қамтиды. (6) функция (1) теңдеудің жалпы шешімі болады. Сонымен, біртектес емес сызықтық теңдеудің жалпы шешімінің құрылымы туралы мынадай теореманы дәлелдедік:

Теорема: Біртектес емес сызықтық теңдеудің жалпы шешімі оның кез келген дербес шешімі мен оған сәйкес келетін біртектес теңдеудің жалпы шешімінің қосындысына тең.

Мысал.

Дербес шешім ретінде аламыз. Сәйкес біртектес теңдеу болады. Оның жалпы шешімі . Сонда берілген теңдеудің жалпы шешімі .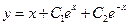

Мысал.

.

.

.

Мысал.

.

.

n реттісызықтық біртектес емес дифференциалдық теңдеулердің жалпы түрі төмендегідей болады:

(7)

мұнда белгілі бір интервалында берілген функциялар. Егер болса, онда (7) теңдеудің мүшелерін

-ке бөлгеннен кейін

(8)

теңдеуіне келеміз. Мұнда

Егер , сегментінде үзіліссіз болса, онда

шарттарын қанағаттандыратындай (8) теңдеудің жалғыз шешімі болатыны ІІ-тарауда көрсетілген. Мұнда (8) теңдеуді қысқа түрде былай жазамыз:

(9)

мұнда .

Теорема 11. Егер функциясы біртектес емес теңдеуінің шешімі болса, ал 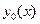сәйкес біртектес теңдеуінің шешімі болса, онда функциясы да біртектес емес теңдеудің шешімі болады.

Дәлелдеуі. Шарт бойынша .

L-операторының сызықтық қасиетінің негізінде

Демек, функциясы теңдеуінің шешімі деген сөз.

Теорема 12. Егер теңдеуінің шешімі болса, онда функциясы теңдеуінің шешімі болады.

Дәлелдеуі. Шарт бойынша

L-операторының сызықтық қасиетін қолданып теңдігін аламыз. Осыдан функциясы теңдеуінің шешімі екені шығады.

Теорема 13. Егер теңдеуінің (мұнда нақтылы мәнді функциялар) функциясы шешімі болса, онда функциялары тиісінше теңдеулерінің шешімі болады.

Дәлелдеуі. Шарт бойынша L-сызықтық оператор болғандықтан Екі комплекс санның теңдігінен

Теорема дәлелденді.

Теорема 14. (Сызықтық бір тектес емес дифференциалдық теңдеудің жалпы шешімінің құрылымы туралы)

D: облысында

(10)

(мұнда )-да үзіліссіз функциялар) теңдеуінің жалпы шешімі оған сәйкес келетін біртектес теңдеудің жалпы шешімі мен оның қандай да бір дербес шешімі -тің қосындысына тең болады, демек

Бұл теореманың дәлелдеу әдісі сызықтық бір тектес дифференциалдық теңдеудің жалпы шешімінің құрылымы туралы теореманың дәлелдеу әдісіне өте ұқсас.

Мысал-2. теңдеуінің жалпы шешімін тап.

1. функциясы берілген теңдеудің шешімі екенің байқау қиын емес.

2. 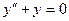біртектес теңдеудің жалпы шешімін іздейміз. Ол үшін сипаттаушы теңдеудің шешімі

3. Ал берген біртектес емес теңдеудің жалпы шешімін мына тұрде немесе табамыз.

Date: 2015-11-15; view: 911; Нарушение авторских прав