
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ДӘРІС 8-9
|
|
Дәріс сабақтың құрылымы:
1 Жоғарғы ретті дифференциалдық теңдеулер
2 Коши есебінің бар және жалғыз болуы туралы теорема
3 Реті төмендетілетін теңдеулердің типтері
Дәріс сабақтың мазмұны:
Жоғары ретті дифференциалдық теңдеулер.
Ретін төмендету әдісі.
Кез келген реті бірден жоғары болатын теңдеулерді реті жоғары дифференциалдық теңдеу деп атайды. Ретін төмендету арқылы интегралдауға болатын қайсыбір дифференциалдық теңдеулер түрлерін қарастырамыз.
І..
 - рет интегралданған соң жалпы шешімін аламыз
- рет интегралданған соң жалпы шешімін аламыз
 .
.
1-мысал.  теңдеудің жалпы шешімін табу керек.
теңдеудің жалпы шешімін табу керек.
Шешуі. Біртіндеп интегралдаймыз:
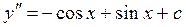 ,
,

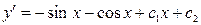

берілген теңдеудің жалпы шешімі.
2-мысал.  теңдеуінің
теңдеуінің 

 бастапқы шарттарды қанағаттандыратын дербес шешімін табыңыз.
бастапқы шарттарды қанағаттандыратын дербес шешімін табыңыз.
Шешуі. Берілген теңдеуді біртіндеп үш рет интегралдаймыз:



Дербес шешімді табу үшін  ді және
ді және  ,
,  ,
,  мәндерін
мәндерін  ,
,  ,
,  өрнектеріне қойып
өрнектеріне қойып 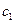 ,
,  ,
,  бойынша жүйені аламыз:
бойынша жүйені аламыз:

Бұл жүйені шешсек:  ,
,  ,
, 
Талап етілген дербес шешімді жазуға болады:

ІІ. Берілген теңдеуде белгісіз функциямен оның алғашқы  ретін қоса есептегендегі туындылары болмайды:
ретін қоса есептегендегі туындылары болмайды:


алмастыруы теңдеудің ретін төмендетуге мүмкіндік береді. Берілген теңдеуді көшіріп жазсақ:

Бұл теңдеуді шешіп

Енді бұл теңдеуді  рет интегралдап
рет интегралдап  -ті анықтауға болады (бұл І түрдегі теңдеу).
-ті анықтауға болады (бұл І түрдегі теңдеу).
3-мысал. Теңдеуді шешіңіз

Шешуі. Бұл теңдеуде белгісіз функциямен оның 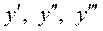 туындылары жоқ. Сондықтан
туындылары жоқ. Сондықтан 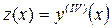 деп ұйғарамыз, сонда
деп ұйғарамыз, сонда  . Ендеше
. Ендеше

Бұл айнымалылары бөлінетін теңдеу
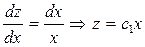
Немесе  . Бұл І түрдегі теңдеу. Біртіндеп интегралдаймыз
. Бұл І түрдегі теңдеу. Біртіндеп интегралдаймыз



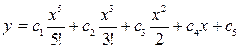
Сонымен ізделген шешімді мына түрде жазуға болады:

ІІІ. Тәуелсіз айнымалы болмайтын теңдеу

алмастыруын жасап теңдеу ретін бірге төмендетеміз. Мұндағы айнымалы  тен тәуелді деп қарастырылады:
тен тәуелді деп қарастырылады:  .
.
Енді теңдеудегі  туындылары арқылы өрнектейміз. Сонда
туындылары арқылы өрнектейміз. Сонда
 ,
,  ,
,

т.с.с,;
Бұл өрнектерді берілген ІІІ теңдеуге апарып қойсақ  - ретті дифференциалдық теңдеу аламыз:
- ретті дифференциалдық теңдеу аламыз:
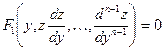 .
.
Егер бұл теңдеуді интегралдау мүмкін болса, онда оның жалпы шешімін былай жазуға болады.

немесе

бұл І-ретті квадратурада интегралданатын дифференциалдық теңдеу.
4- мысал.  теңдеуін шешміз.
теңдеуін шешміз.
Шешеуі.  деп ұйғарамыз. Сонда
деп ұйғарамыз. Сонда  болады. Демек,
болады. Демек,

Бұл Бернулли теңдеуі, егер 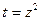 деп алсақ ол сызықтық теңдеу болады.
деп алсақ ол сызықтық теңдеу болады.

Жалпы шешімі

Енді  -ның орнына қоямыз:
-ның орнына қоямыз:

Айнымалыларын бөліп, интегралдаймыз:

Немесе берілген теңдеудің жалпы шешімін мына түрде жазуға болады:
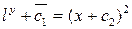 ,
, 
Өзін-өзі тексеруге арналған сұрақтар:
1 Жоғарғы ретті дифференциалдық теңдеулер
2 Реті төмендетілетін теңдеулердің типтері
Қолданылған әдебиеттер:
1. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.- М.: Наука, 1985
2. Қалиев С.Қ., Искакова М.Т. Дифференциалдық теңдеулер және варияциялық есептеу негіздері, Семей – 2005
3. Филлипов А.Ф. Сборник задач по обыкновенные дифференциальным уравнениям. М.: Наука, 1984
4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - Москва.: Изд-во МГУ, 1984.
5. Қадыкенов Б.М. Дифференциалдық теңдеулердің есептері мен жаттығулары Алматы: Қазақ университеті, 2002
Date: 2015-11-15; view: 2544; Нарушение авторских прав