
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ДӘРІС 3-4
|
|
Дәріс сабақтың құрылымы:
1 Біртектес теңдеулер
2 І-ретті сызықтық дифференциалдық теңдеулер
3 Бернулли теңдеуі
4 Толық дифференциалдағы теңдеулер. Интегралдаушы көбейткіш
Дәріс сабақтың мазмұны:
Анықтама 6. Егер кез келген к үшін 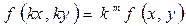 теңдігі орындалса, онда
теңдігі орындалса, онда  функциясын m дәрежелі біртектес функция деп атайды.
функциясын m дәрежелі біртектес функция деп атайды.
Мысалға,  функциясы үш дәрежелі біртектес функция, өйткені
функциясы үш дәрежелі біртектес функция, өйткені  .
.  функциясы «0» дәрежелі біртектес функция, себебі кез келген
функциясы «0» дәрежелі біртектес функция, себебі кез келген 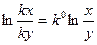 . “0” дәрежелі біртектес функцияны
. “0” дәрежелі біртектес функцияны  қатынасының функциясы ретінде өрнектеуге болатынын көрсетейік.
қатынасының функциясы ретінде өрнектеуге болатынын көрсетейік.
Айталық,  “0” дәрежелі біртектес функция болсын.
“0” дәрежелі біртектес функция болсын.  деп алайық. Сонда анықтама бойынша
деп алайық. Сонда анықтама бойынша
 (8)
(8)
Айталық,  функциясы m дәрежелі біртектес функция болсын. Онда
функциясы m дәрежелі біртектес функция болсын. Онда  функциясы “0” дәрежелі біртектес функция болатыны көрінеді. Онда жоғарыдағы тұжырымның негізінде
функциясы “0” дәрежелі біртектес функция болатыны көрінеді. Онда жоғарыдағы тұжырымның негізінде 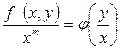 , осыдан
, осыдан  . Бұл өрнектеу m дәрежелі біртектес функцияның жалпы түрі болып табылады.
. Бұл өрнектеу m дәрежелі біртектес функцияның жалпы түрі болып табылады.
Анықтама 7. Егер  және
және 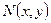 функциялары бірдей дәрежелі біртектес функциялар болса, онда
функциялары бірдей дәрежелі біртектес функциялар болса, онда  теңдеуі бірінші ретті біртектес теңдеу деп аталады.
теңдеуі бірінші ретті біртектес теңдеу деп аталады.
Біртектес теңдеулер  (немесе
(немесе  ) алмастыруы арқылы айнымалысы ажыратылатын теңдеуге келтіріледі. Шынында да (6) теңдіктің көмегімен (8) теңдеуді былай түрлендіреміз:
) алмастыруы арқылы айнымалысы ажыратылатын теңдеуге келтіріледі. Шынында да (6) теңдіктің көмегімен (8) теңдеуді былай түрлендіреміз:
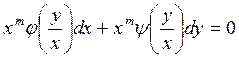
 болғандықтан, қысқарту арқылы
болғандықтан, қысқарту арқылы 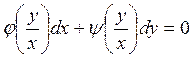 теңдеуін аламыз.
теңдеуін аламыз.  десек, осыдан,
десек, осыдан,  . Осыларды соңғы теңдеуге апарып қойсақ
. Осыларды соңғы теңдеуге апарып қойсақ  теңдеуін аламыз, немесе
теңдеуін аламыз, немесе  . Сөйтіп, айнымалысы ажыратылатын теңдеуге келтірдік.
. Сөйтіп, айнымалысы ажыратылатын теңдеуге келтірдік.
Енді айнымалысын ажырату арқылы  теңдеуіне келеміз. Осыдан
теңдеуіне келеміз. Осыдан  . Потенциалдау арқылы мына түрде жазамыз,
. Потенциалдау арқылы мына түрде жазамыз, 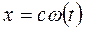 немесе
немесе  -бұл соңғы нәтиже.
-бұл соңғы нәтиже.
Біртектес теңдеудің интегралдық қисықтары бір-біріне ұқсас болады. Ұқсастық центрі координаттың бас нүктесінде орналасқан.
Мысал-4.  теңдеуін шеш. Мұнда
теңдеуін шеш. Мұнда  . Бұл функциялар екінші ретті біртектес функциялар. Ендеше берілген теңдеу біртектес теңдеу болады.
. Бұл функциялар екінші ретті біртектес функциялар. Ендеше берілген теңдеу біртектес теңдеу болады.  деп алып
деп алып  және
және  шамаларын ауыстырамыз (алмастырамыз)
шамаларын ауыстырамыз (алмастырамыз)




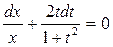
интегралдау арқылы  .
.
Потенциалдап  теңдігін аламыз.
теңдігін аламыз.  -ны
-ны  -ке ауыстырсақ
-ке ауыстырсақ  .
.
Әрі қарай түрлендірсек  .
.
Бұл теңдеу центрі  нүктeсінде, ал радиусы
нүктeсінде, ал радиусы  -ке тең болатын шеңберлер үйірі болып табылады.
-ке тең болатын шеңберлер үйірі болып табылады.
 теңдеуін қарастырайық. Бұл теңдеу біртектес теңдеуге келтірілетін теңдеу. Мұнда
теңдеуін қарастырайық. Бұл теңдеу біртектес теңдеуге келтірілетін теңдеу. Мұнда  –тұрақтылар, ал
–тұрақтылар, ал 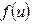 –функциясы өзінің аргументі бойынша үзіліссіз функция. Егер
–функциясы өзінің аргументі бойынша үзіліссіз функция. Егер  болса берілген теңдеу біртектес болатыны көрініп тұр. Сондықтан
болса берілген теңдеу біртектес болатыны көрініп тұр. Сондықтан  мен
мен 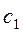 -дің кемінде біреуі нольден өзгеше болады деп есептейміз.
-дің кемінде біреуі нольден өзгеше болады деп есептейміз.
Екі жағдайды айырып қараймыз.
10.  , осы жағдайда
, осы жағдайда  ауыстырымын енгізу арқылы берілген теңдеуді біртектес теңдеуге келтіруге болады. Мұнда
ауыстырымын енгізу арқылы берілген теңдеуді біртектес теңдеуге келтіруге болады. Мұнда 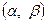
 (*)
(*)
теңдеулер жүйесінің шешімі. Енді x,y және y /-ты жаңа айнымалылармен ауыстыру арқылы берілген теңдеу 
теңдеуіне түрленеді. Ал соңғы теңдеу біртектес, оның шешімін табуды білеміз.
20.  . Бұл жағдайда (*) системасының жалпы алғанда шешімі болмайды.
. Бұл жағдайда (*) системасының жалпы алғанда шешімі болмайды.
Егер  деп алсақ, берілген теңдеу айнымалысы ажыратылатын теңдеуге айналады.
деп алсақ, берілген теңдеу айнымалысы ажыратылатын теңдеуге айналады.
Мысал-5.  теңдеуін шеш.
теңдеуін шеш.
 -ты
-ты  пен ауыстырып,
пен ауыстырып, 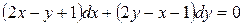 теңдікке келеміз.
теңдікке келеміз.  системасын құрамыз. Системаның анықтауышы:
системасын құрамыз. Системаның анықтауышы: 
Системаның жалғыз ғана шешімі болады, демек,  .
.
x және y айнымалыларының орнына жаңа айнымалылар s пен r -ді төмендегі қатыс арқылы енгіземіз.  осыдан
осыдан 
x, y,  -ті жаңа айнымалылар арқылы ауыстырсақ
-ті жаңа айнымалылар арқылы ауыстырсақ  біртектес теңдеу шығады. Әрі қарай,
біртектес теңдеу шығады. Әрі қарай,  айнымалысын енгізіп, теңдеуді шешеміз, нәтижесінде
айнымалысын енгізіп, теңдеуді шешеміз, нәтижесінде  теңдігін аламыз. (түрлендірулерді өздерің жүргізіңдер).
теңдігін аламыз. (түрлендірулерді өздерің жүргізіңдер).
Ақырында r,s айнымалыларын ескі x пен y айнымалылары арқылы өрнектен  жалпы интегралды табамыз.
жалпы интегралды табамыз.
Анықтама 8.
у'+p(x)y=q(x) (9)
түріндегі теңдеуді бірінші ретті сызықтық дифференциалдық теңдеу деп атайды.
Мұнда р(х),g(х) үздіксіз функциялар.
Байқасаңдар, у ' туындысы функция у -тің сызықтық функциясы. Сондықтан да сызықтық теңдеу деп аталған.
 Егер g(x)
Егер g(x)  0 - са, онда (9) теңдеу айнымалысы ажыратылатын теңдеуге айналады. Жалпы жағдайда (9) теңдеудің айнымалысы ажыратылмайды.
0 - са, онда (9) теңдеу айнымалысы ажыратылатын теңдеуге айналады. Жалпы жағдайда (9) теңдеудің айнымалысы ажыратылмайды.
Сондықтан (9) теңдеудің өзіне тән шығару әдісін көрсетеміз. Ол үшін белгісіз функцияны у=uv (*) түрінде іздейміз, мұнда u(x) және v(x) дифференциялданатын функциялар.Туындыны табамыз.
у'=u'v+uv'
Енді осы өрнектерді (9) теңдеуге қойып, оны мына түрге келтіруге болады.
u'v+u(v'+p(x))=q(x) (10)
v- функциясын v'+p(x)v өрнегін x -ке қарағанда тепе–теңдікке айландыратындай етіп таңдап аламыз. Ондай функция
v'+p(x)v=0 (11)
теңдеудің шешімі бола алады.
(11)- теңдеудің бір ғана шешімін табу жеткілікті.
Мысалға, ондай шешім:
 (12)
(12)
болады.
Ал у=uv функциясы (10) теңдеудің шешімі болу үшін u- функциясы u'v0(x)=q(x) немесе
 (13)
(13)
теңдеуінің шешімі болуға тиіс. (1.18) теңдеуді шешеміз


Енді v және u фунцияларының өрнегін (*) теңдікке апарып қойсақ,
 (14)
(14)
іздеп отырған шешімді табамыз. (1.19)-формуланы мына түрде де
 (15)
(15)
жазуға болады.
Бірақ бұл жағдайда формулаға кіретін әрбір анықталмаған интегралды бір ғана алғашқы функция ретінде қарастырған жөн болады.
(14) немесе (15) формулаларын осылай қорыту әдісін Бернулли әдісі деп атайды.
Сөйтіп сызықтық теңдеуді шешу (шығару) үшін қорытылған (14) немесе (15) формулаларын пайдалануға болады. Алайда Бернулли әдісін әрбір теңдеуге тікелей қолдану арқылы да шешеді.
Бернулли әдісін көрсету барысында байқағанымыздай сызықтық теңдеудің шешімін табу төмендегі дифференциалды теңдеулер системасына келіп тіреледі.
 (16)
(16)
Системаны құрайтын теңдеулердің екеуі де айнымалысы ажыратылатын теңдеулер. Біріншісін шешіп v функциясын табамыз. Табылған функцияны екіншісіне қойып u функциясын анықтаймыз. Соңында
y=u·v
түріндегі берілген сызықтық теңдеуінің шешімі табылады.
Мысал-6. y'+3y=e2х мұнда р(x)=3, q(x)=e2х. (15) формуласын пайдаланып шешейік.
y=e 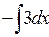 (
( 2x·e
2x·e  dx+C)=e-3x(
dx+C)=e-3x( 2x·e3xdx+c)=e-3x(1/5e5x+C)
2x·e3xdx+c)=e-3x(1/5e5x+C)
Сөйтіп,
y= 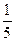 e2x+Ce-3x
e2x+Ce-3x
Мысал-7. y'+2xy=xe-x 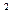 -теңдеуінің жалпы шешімін табу керек.
-теңдеуінің жалпы шешімін табу керек.
Мұнда p(x)=2x, q(x)=xe-x 

Бұл теңдеуді (16) ситеманы құру арқылы шығарайық.

Бірінші теңдеудің бір ғана шешімі жеткілікті.
 =-2xdx, lnv=-x2 v=e-x
=-2xdx, lnv=-x2 v=e-x 
Екінші теңдеуге v функциясының өрнегін қойып, оны шешеміз.
u/e-x  =xe-x
=xe-x  , u/=x u=x2/2+C
, u/=x u=x2/2+C
Сөйтіп, берілген теңдеудің жалпы шешімі y= e-x  (x2/2+C) функциясы.
(x2/2+C) функциясы.
Date: 2015-11-15; view: 903; Нарушение авторских прав