Анықтама 9

y'+p(x)y=y q(x) (17)

теңдеуді Бернулли теңдеуі дейді. Мұнда кез келген нақты сан.

Егер =0 –болса, онда (17) теңдеу сызықтық теңдеуге, ал =1 болса, айнымалысы ажыратылатын теңдеуге айналады. Сондықтан 0,1 деп есептейміз.

Бернулли теңдеуі сызықтық теңдеуге келтірілетін теңдеуге жатады.

Егер (17) теңдеудің екі жағын y бөлсек, онда

y^- y'+p(x)y^1- =q(x) (18)

теңдеуін аламыз. z=y^1- десек, z'=y^- y'(1- )

Сонда y^- y'= . Енді (18) теңдеуге қойсақ,

(19)

теңдеуі шығады. (19) теңдеудің z айнымалысына қарағанда сызықтық екені көрініп тұр. (17) теңдеудің де шешімін y=u·v түрінде іздейміз. Бернулли әдісі бойынша теңдеуді түрлендіріп

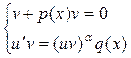(20) системасын алуға болады. Бірінші теңдеуді шешіп v -ны, екінші теңдеуді шешіп u –ды табамыз.

Мысал-8. y'+y/x=-2x²y² теңдеуінің жалпы шешімін тап.

p(x)=1/x, q(x)=-2x², =2

(24) системаны құрамыз: y=u·v

Бірінші теңдеуді шешсек , ,

, ; ;

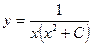
F(x,y) eкі айнымалы функцияның толық дифференциалы

dF(x,y)= dx+ dy

түрінде анықталатыны белгілі.

Егер

M(x,y)dx+N(x,y)dy (21)

өрнегі берілсе, онда (21) өрнек қай жағдайда қандайда бір функцияның толық дифференциалы болады деген табиғи сұрақ өзінен-өзі туады. Басқаша айтсақ,

=M(x,y) және =N(x,y)

теңдіктері орындалатындай F(x,y) функциясы бар болатынын қалай білуге болады деген сөз.

Бұл сұраққа төменде дәлелденетін теорема жауап береді. Біз былайғы жерде M(x,y) және N(x,y) функцияларының белгілі бір D облыста үзіліссіз дербес туындылары бар деп есептейміз.

Теорема 2 (21) өрнек D облыста анықталған екі айнымалы функциясы F(x,y) -тің толық дифференциалы болу үшін

= (22)

теңдігінің осы D облысында орындалуы қажетті және жеткілікті.

Дәлелдеуі 1) Алдымен (22) шарттың қажеттілігін дәлелдейік.

Ол үшін (21) өрнек қандайда бір F(x,y) функциясының D облысында толық диффернциалы деп жорыйық, демек

M(x,y) dx+N(x,y) dy =dF(x,y)

Бұл жағдайда =M(x,y) және =N(x,y) болатыны белгілі. M(x,y) және N(x,y) функцияларының дербес туындысын табайық.

және (23)

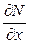Шарт бойынша және D облысында үзіліссіз. Ендеше екінші ретті аралас туындылар

және

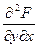
D облысында үзіліссіз болады.

Анализден белгілі теорема бойынша

= , . Осыдан теңдігі шығады

2) (22) шарттың жеткіліктігін дәлелдейік.

Айталық, = , . Осы жағдайда (21) өрнек қандайда бір функцияның толық дифференциалы болатынын көрсетейік. Ол үшін

F(x,y)= + (24)

деп белгілейік. Мұнда әзірше белгісіз функция. (24) формуладан

= M(x,y), (25)

болатынын көреміз.

Eнді

= N(x,y) (26)

болатындай етіп, функциясын табамыз. (24) теңдікті y айнымалысы бойынша дифференциалдап (26) теңдікті мына түрде

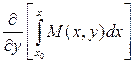+ = N(x,y) (27)

жазамыз.

М(x,y) және үзіліссіз функциялар болғандықтан (27) теңдікті мына түрде + = N(x,y) жазуға болады. Соңғы теңдіктен -ті табамыз.

= N(x,y) - (28)

Егер (28) теңдіктің оң жағы x -ке тәуелсіз болса, онда іздеп отырған функциямыз -ті (28) теңдіктің екі жағын интегралдау арқылы тауып аламыз.

Шынында да, (28) теңдіктің оң жағы x -ке тәуелсіз екенін (22) теңдіктің негізінде көрсетейік:

Демек, (28) теңдіктің оң жағы x - ке тәуелсіз. Енді (28) және (26) теңдіктердің негізінде

dF(x,y) = dx+ dy= M(x,y) dx +N(x,y) dy,

екенін көреміз.

Анықтама 10. Егер

M(x,y) dx +N(x,y) dy =0 (29)

теңдеуінің сол жағы екі айнымалы функциясының толық дифференциалы болса, онда (29) теңдеуді толық дифференциал теңдеу дейміз.

Анықтамада айтылған функцияны F(x,y) деп белгілесек, (29) теңдеуді былай жазуға болады. dF(x,y)=0

Бұл теңдеудің шешімі F(x,y)=C болатыны белгілі. Осыдан толық дифференциал теңдеуді шешу, ол теңдеудің оң жағының толық дифференциалы болатын функцияны табуға келіп тіреледі екен.

Мұндай функция жоғарыдағы дәлелденген теореманың дәлелдеу жолы бойынша табылады.Оны төмендегі мысалмен көрсетеміз.

Мысал-9. (6 x² y² + 6 xy –1) dx +(4 x³ y +3 x² +2 y) dy=0

теңдеуінің жалпы шешімін тап.

M(x,y) =6 x² y² + 6 xy –1, N(x,y) =4 x³ y +3 x² +2 y

Берілген теңдеудің толық дифференциaл теңдеу екенін тексереміз, демек

= көрсетеміз.

= 12 x² y + 6 x

= 12 x² y + 6 x

Осыдан толық дифференциал теңдеу екені шығады. (24) формулада интеграл шегі x₀ -ді кез келген жолмен таңдап алатын болғандықтан, демек (24) формула М(х,у) функциясының кез келген алғашқы функциясы үшін орындалатындықтан анықталған интегралдың орнына сәйкес анықталмаған интегралды жазсақ та болады.

Сонымен,

F(x,y) = (6 x² y² + 6 xy –1)dx + = 2 x ³y² + 3 x ²y – x + (*)

-ті табу үшін (1.31) формуланы пайдаланамыз.

4 x³ y +3 x²+ =4 x³ y +3 x² +2 y

Осыдан = 2y = y²+C₁

Енді (*) теңдіктегі -тің орнына қойып

F(x,y)= 2 x ³y² + 3 x ²y – x+ y²+C₁

теңдігін аламыз.

Жалпы шешім

2 x ³y² + 3 x ²y – x+ y²+C₁ =C₂ немесе 2 x ³y² + 3 x ²y – x+ y²=C

Айталық,

P(x,y) dx +Q(x,y) dy =0 (30)

теңдеу толық дифференциал теңдеу болмасын, алайда осы теңдеуді бір m (x,y) функциясына көбейткеннен шыққан теңдеу.

M(x,y) dx +N (x,y) dy =0, M(x,y) =p(x,y) m (x,y)

N (x,y)= Q(x,y) m (x,y); толық дифференциал теңдеу болып шықса,

m(x,y) функциясын (30) теңдеудің интегралдаушы көбейткіші деп атайды.

Мысалға, M₁(x) M₂(y) dx +N₁(x) N₂(y) dy=0

айнымалысы ажыратылатын теңдеудің интегралдық көбеткіші m (x,y)= функциясы болады. Демек осы көбейткішке көбейткеннен шыққан теңдеу толық дифференциал теңдеу болады. (өздерің дәлелдеңдер)

Сондай-ақ y¢+p(x)y = q(x) сызықтық теңдеудің интегралдық көбейткіші функциясы болатынын көрсету қиын емес.

Сөйтіп, біз бұрынырақ қарастырған теңдеулерді толық дифференциал теңдеуге келтіру арқылы шығаруға болады екен.

Тағы бір ескертетін жағдай бір ғана дифференциалдық теңдеу үшін бірнеше интегралдық көбейткіш бар болуы мүмкін. Мысалға 2ydx +xdy=0 теңдеуін алайық. Осы теңдеу үшін m₁ (x,y)=x, m₂ (x,y) = , m ₃(x,y) функциялары интегралдық көбейткіштер болады. (Осыны дәлелдеңдер)

Өкінішке орай, кез келген теңдеу үшін интегралдық көбейткіштерді табудың ортақ әдісі жоқ. Кейбір дербес теңдеулер үшін интегралдық көбейткіш табудың дербес әдістері бар.

Өзін-өзі тексеруге арналған сұрақтар:

1 Біртектес теңдеулер

2 Сызықтық теңдеулер

3 Бернулли теңдеуі

4 Толық дифференциалдағы теңдеулер

Қолданылған әдебиеттер:

1. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.- М.: Наука, 1985

2. Қалиев С.Қ., Искакова М.Т. Дифференциалдық теңдеулер және варияциялық есептеу негіздері, Семей – 2005

3. Филлипов А.Ф. Сборник задач по обыкновенные дифференциальным уравнениям. М.: Наука, 1984

4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - Москва.: Изд-во МГУ, 1984.

5. Қадыкенов Б.М. Дифференциалдық теңдеулердің есептері мен жаттығулары Алматы: Қазақ университеті, 2002