Глава 3. Элементы аналитической Геометрии 4 page

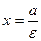
Для гиперболы:

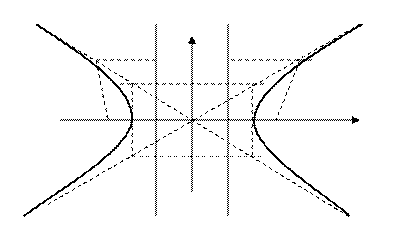
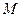
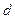
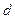
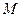
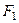
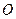
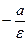
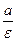
Основное свойство директрис: если 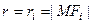- рас -стояние до ближайшего фокуса, а 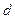- расстояние до соот -ветствующей директрисы , то .

Таким образом, с помощью основного свойства директрис, эллипс и гиперболу можно определить, как множества точек, для которых отношение расстояний до фокуса и до соответс- твующей директрисы - величина постоянная, равная эксцент- риситету 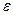, причём для эллипса 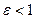, а для гиперболы 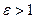. В случае 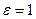получаем ещё одну линию - параболу.

4. Парабола. Параболой называется геомнтрическое место точек плоскости, равноудадённых от данной точки, называемой фокусом и данной прямой, называемой директрисой.

Введём на плоскости систему координат: ось проходит через фокус перпендикулярно директрисе. Ось 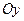перпендику- лярна оси и проходит на одинаковом расстоянии между от фокуса и директрисы. Пусть расстояние от фокуса до ди –ректрисы равно

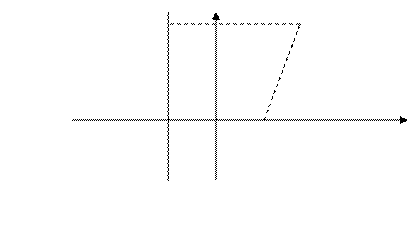
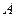
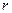
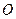
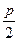
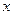
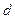
По определению параболы, расстояние от фокуса до точки равно длине отрезка . Тогда 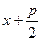. Возведём в квадрат это равен- ство: . Таким образом, полу- чаем каноническое уравнение параболы:

(9)

Построим эту линию. Она симметрична относительно оси (так как входит в уравнение в чётной степени).

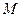
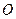
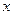
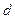
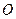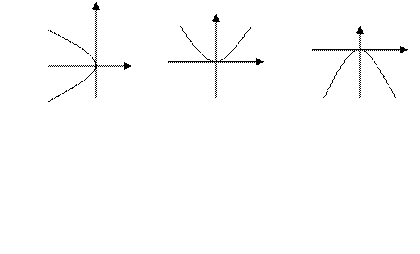
Точка является вершиной параболы, ось - ось её сим- метрии. Кроме параболы , можем рассмотреть ещё параболы 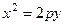и , которые вы – глядят, соответственно, следующим образом:

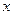
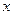
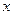
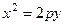
Рассмотрим пример. Привести к каноническому виду уравне- ние следующей линии и построить её:

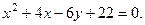
Преобразуем это уравнение:

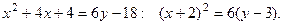
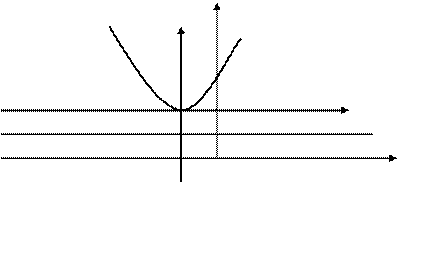Вершина параболы находится в точке 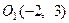. . 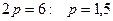Построим эту линию.

.

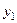
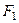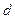
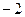
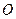
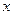
Оптическое свойство параболы: Если источник света рас -положен в фокусе параболы, то отражённый луч распространя- ется по прямой

Мы рассмотрели основные линии второго порядка.

Рассмотрим теперь пример полного преобразования уравне- ния линии 2 – го порядка с помощью параллельного переноса и поворота системы координат.

Привести к каконическому виду уравнение линии. Выпол- нить построение линии:

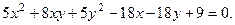
Выполним параллельный перенос системы координат по формулам (2): 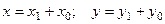. Получим:

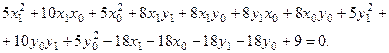
С помощью параллельного переноса мы должны избавиться от линейных слагаемых в уравнении, т.е. приравниваем нулю:

Эти равенства должны выполняться для всех 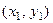, т.е. получаем систему:

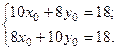Тогда: 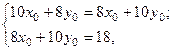или

Таким образом, перенос системы координат необходимо произвести в точку . При этом получим уравнение:

Чтобы избавиться от смешанного произведения , выпол- ним поворот системы координат по формулам (4):

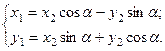
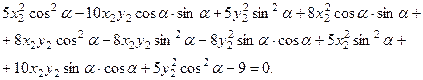
Нам необходимо убрать смешанное произведение, поэтому группируем соответствующие коэффициенты и приравниваем их к нулю:

Учитывая тригонометрические формулы, получаем:

.

Перепишем уравнение линии, с учётом того, что смешанного произведения в уравнении не осталось:

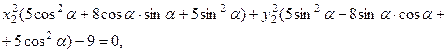или, 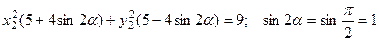и тогда: и, окончательно,

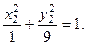
Получили каноническое уравнение эллипса с полуосями

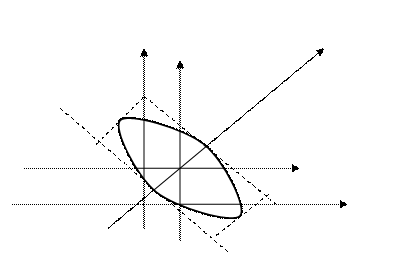
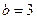. Построим данную линию:

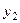
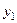
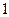
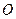1

1

Рассмотрим ещё примеры: Пример 1. Построить следующую линию: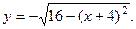

Из уравнения видим, что должно быть выполнено: 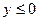. Возведём равенство в квадрат: 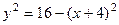. Тогда Получено уравнение окружности с центром в точке радиуса 4.

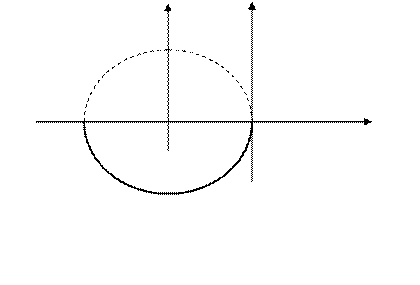
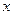
С учётом условия 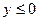, мы получаем нижнюю часть окруж –ности.

Пример 2. Построить линию:

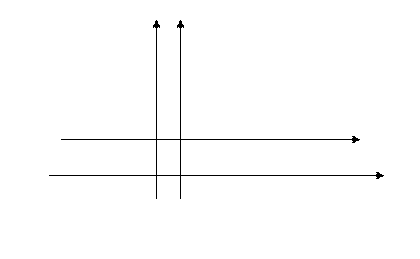
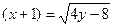. Ограничение: 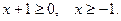Возведём последнее равенство в квадрат . Это урав- нение параболы с вершиной в точке 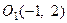. . Построим линию:

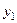
2

-1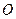

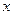
Ввиду условия 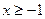, выбираем правую ветку параболы.

§ 7 ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ.

Полярная система координат на плоскости определяется за- данием некоторой точки 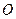, называемой полюсом; исходящего из этой точки луча , называемого полярной осью и мас -штабной единицей для измерения длин.

Для произвольной точки 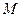плоскости координатами в дан- ной системе координат называют полярный радиус 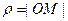, вычисленный в масштабных единицах, и полярный угол 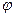между осью 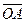и радиус – вектором , т.е. ,

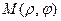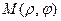
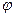
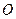1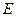

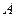
Чаще всего предполагают, что 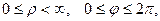или 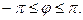Иногда допускаются отрицательные значения для , но при этом соответствующие значения откладываются на продолжении луча.

Установим связь между полярными координатами точки и её декартовыми координатами. Для этого совместим начало декартовой системы координат с полюсом полярной системы координат, а ось - с полярной осью:

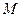
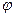
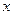
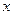
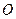
Используя тригонометрические формуды легко получаются формулы перехода от декартовых координат к полярным:

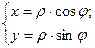(1)

и формулы обратного перехода от полярных координат к де- картовым:

(2)

Чаще всего эти формулы используются комбминированно.

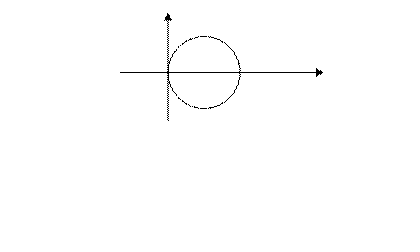
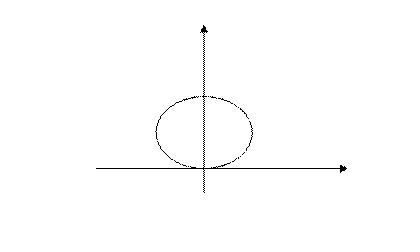
Окружность 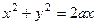в полярной системе координат имеет уравнение 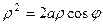, или , тогда дпнная линия имеет вид:

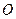
Аналогичным образом, окружность имеет в полярных координатах уравнение 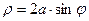и соответству- ющий рисунок линии выглядит следующим образои:

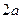
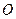
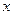
Окружность с центром в начале координат в полярных координатах имеет уравнение или .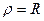

Если задано уравнение линии в полярных координатах 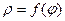, то чтобы построить данную линию в полярной сис- теме координат, заполняют таблицу значений этой функции в точках, вычисленных для значений аргумента 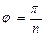, причём, чем больше , тем точнее будет построение линии.

Пример 1. Построить линию: .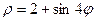

Заполнить таблицу значений данной функции:

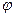
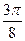
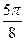
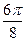
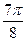
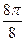
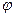
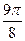
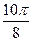
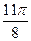
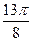
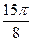
Построим данную линию

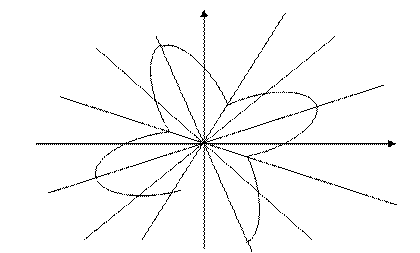
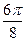
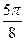
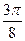
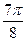
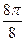
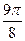
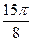
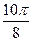
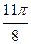
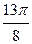
При построении линии в полярных координатах можно по -ступать и иначе, а именно, используя свойства соответствую- щих функций.

Пример 2. Пусть дано уравнеие 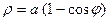. Так как , то максимальное значение данная функция принимает при - ; мини –мальное значение будет в точке - .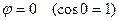

Так как 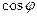чётная функция, то 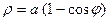также чётная функция и поэтому соответствующая линия симме- трична отностьельно полярной оси. Таким образом, получаем линию:

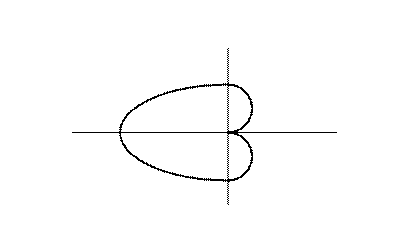
Date: 2015-12-10; view: 478; Нарушение авторских прав