Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
I. Уравнение поверхности
|
|
Уравнение F(x, y) = 0 определяет на плоскости некоторую линию, т. е. множество всех точек плоскости Оху, координаты которых х и у удовлетворяют этому уравнению. Подобно этому уравнение
F(x,y,z) = 0, (1) определяет в пространстве Охуz некоторую поверхность, т. е. множество всех точек, координаты которых х, у, z удовлетворяют уравнению F(x, у, z) = 0. Уравнение (1) называется уравнением этой поверхности, а х, у, z — ее текущими координатами. Часто, однако, поверхность задается не уравнением, а как мно- жество всех точек, обладающих тем или иным свойством. В этом случае требуется найти уравнение поверхности, исходя из ее геометрических свойств.
Пример. Найти уравнение сферы радиуса R с центром в точке 
Решение. Согласно определению сферы, расстояние любой ее точки М (х,у, z) от центра 
равно радиусу R, т. е. 
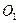M=R. Но
Следовательно, 
или
(2)
Мы получили искомое уравнение сферы, так как ему удовлетворяют координаты любой ее точки и, очевидно, не удовлетворяют координаты точек, не лежащих на данной сфере.
В частности, если центр сферы совпадает с началом координат, то уравнение сферы примет следующий вид:
.
Раскрыв скобки и перенеся все члены в левую часть уравнения (2), получим
Это уравнение второй степени относительно текущих координат х, у и z. В нем отсутствуют члены с произведениями координат, а коэффициенты при х2 , у2 и z2 равны между собой. Любое уравнение второй степени относительно х, у и z, в котором коэффициенты при х2, y2 и z 2 равны между собой, а член с произведением координат отсутствует, есть, вообще говоря, уравнение сферы. Точнее, такое уравнение с помощью выделения полных квадратов всегда может быть приведено к виду:
. (3)
Если при этом 
>0, то уравнение (3) является уравнением сферы с центром в точке и радиусом R = 
. При k = 0 уравнению удовлетворяют координаты лишь одной точки . Если же <0, то уравнение не определяет никакой поверхности.
Пример. Доказать, что уравнение
является уравнением сферы, и найти центр и радиус этой сферы.
Решение. Преобразуя левую часть данного уравнения, полу- чим
или 
.
Мы получили уравнение сферы с центром в точке О(1; - 2; - 3) и радиусом R = 4.
Date: 2015-12-10; view: 398; Нарушение авторских прав