Нехай задана послідовність чисел

Ряд

(1)

називається степеневим рядом. Числа - коефіцієнти степеневого ряду. Покладемо в (1) 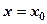, отримаємо числовий ряд

(2)

Якщо числовий ряд збіжний, то про степеневий ряд (1) говорять, що він збігається в точці .

Означення. Множина значень , для яких ряд (1) збігається називається областю збіжності степеневого ряду.

Структура області збіжності степеневого ряду обгрунтовується за допомогою теореми Абеля.

Теорема ( Абеля ). 1) Якщо степеневий ряд (1) збіжний в точці 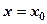(), то він абсолютно збіжний для всіх , що .

Якщо степеневий ряд розбіжний в точці , то він розбігається для всіх значень таких .

Доведення. 1) Згідно з умовою теореми при 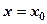отримаємо збіжний ряд (2), для якого згідно з необхідною ознакою збіжності

.

А це означає, що всі члени цього ряду є обмеженими, тобто існує число таке, що для всіх

. (3)

Розглянемо тепер ряд із абсолютних величин ряду (1)

(4)

.

Відповідно до нерівності (3) запишемо новий ряд

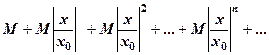(5)

Позначимо . Згідно умови теореми , тому 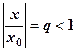. Отже, ряд (5) є сумою нескінченно спадної геометричної прогресії, а, значить, збіжний. За ознакою порівняння ряд (4) теж збігається.

Друга частина теореми доводиться від супротивного. Подальше доведення опускаємо.

За допомогою теореми Абеля вияснимо область збіжності степеневого ряду (1). Для цього розглянемо додатний ряд (4), до якого застосуємо ознаку Даламбера:

,

Позначимо через останню границю, тобто

, (6)

яку назвемо радіусом збіжності Згідно теореми Абеля степеневий ряд збігається абсолютно для всіх

.

Отже частиною області збіжності є інтервал . Щоб отримати повністю всю область збіжності степеневого ряду необхідно окремо дослідити збіжність рядів в точках

і .

Приклад. Знайти області збіжності степеневих рядів.

.

Розв’язання. 1. Знайдемо радіус збіжності , тобто ряд абсолютно збігається в інтервалі .

Перевіримо збіжність в точках .

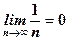При маємо За ознакою Лейбніца , ряд збіжний.

При маємо - гармонійний розбіжний ряд. Отже, областю збіжності даного степеневого ряду є .

2. , . За формулою (6) .

Отже, степеневий ряд збігається на всій числовій осі.

3. , , . : - ряд розбіжний.

Аналогічно, розбіжний для .Отже, область збіжності .

Приклади. Знайти область збіжності кожного з поданих рядів.

1. 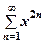.	2. .
3. .	4. .
5. .	6. .
7. .	8. .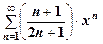

Date: 2015-12-10; view: 381; Нарушение авторских прав