Ознака порівняння

Теорема. Нехай задано два ряди. (1) і 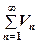(2), причому члени першого ряду не перевищують відповідних членів другого ряду, тобто для довільних n

. (3)

Тоді:

1) із збіжності ряду (2) випливає збіжність ряду (1);

2) із розбіжності ряду (1) випливає розбіжність ряду (2).

Доведення. 1) Нехай ряд (2) збіжний, тобто існує границя

.

Згідно з нерівністю (3) для часткових сум ряду (1) маємо нерівність

.

Із додатності рядів очевидно, що часткові суми монотонно зростають. Скористаємось ознакою існування границь: якщо послідовність монотонно зростає і обмежена зверху, то вона має границю.

Поскільки 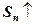і , то існує . Отже, ряд (1) збіжний.

2) Якщо ж додатний ряд (1) розбіжний, то при , а, значить, із нерівності , тобто ряд (2) теж розбіжний.

Приклади. Дослідити збіжність рядів.

1. .

2. .

3. .

4. .

Розв’язання. 1. Поскільки 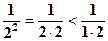, , …, , , … то із збіжності ряду (див. ряд (5) в 1.) за ознакою порівняння випливає збіжність ряду

,

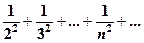приписавши в останньому ряді спереду доданок 1, отримаємо початковий ряд , який збігається.

2. Поскільки а праві частини цих нерівностей є членами гармонічного ряду , який розбігається, то за ознакою порівняння ряд 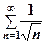теж розбігається.

3. Із нерівності і збіжності отримуємо збіжність ряду .

4. Аналогічно попередньому маємо , якщо . Отже, ряд теж збіжний при .

В більшості випадків зручнішою може бути гранична ознака порівняння, яку подаємо без доведення.

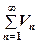Теорема (гранична ознака порівняння). Нехай задані ряди (1) і (2).

Якщо існує скінчена границя відношення загальних членів, відмінна від 0, тобто

,

то обидва ряди ведуть себе однаково, тобто або одночасно збігаються або одночасно розбігаються.

Приклади. Дослідити збіжність ряду.

1. . 2. .

Розв’язання. 1. З теорії границь відомо, що при многочлен веде себе так, як його найстарший доданок, тобто 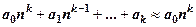при . Тому , а . Візьмемо , а .

Розглянемо

.

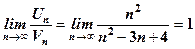Відповідно теоремі обидва ряди і збіжні, бо збіжність другого ряду вже доведена.

2. Поскільки при 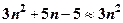, а , то .

Тому знаходимо границю

.

Ряд 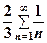- є гармонічним, розбіжним, тому розбіжним є і даний ряд.

Date: 2015-12-10; view: 452; Нарушение авторских прав