Інтегральна ознака Коші

Теорема (Коші, інтегральна). Нехай дано ряд , члени якого не зростають, тобто

,

і існує незростаюча неперервна на функція така, що

,

то ряд і невласний інтеграл одночасно або збігаються або розбігаються.

Рис.1 Рис.2

і ступінчатих фігур (див. рис.1 і рис.2)

Із рис.2 маємо нерівність

.

А із рис.1 нерівність протилежного характеру

,

звідки отримуємо

.

З лівої нерівності маємо, що із існування границі , тобто, із збіжності ряду випливає існування границі

-

- збіжність невласного інтеграла. Аналогічно права нерівність стверджує, що із збіжності невласного інтеграла випливає збіжність ряду.

Подібні міркування застосовуються на випадок розбіжності.

Приклад. Дослідити збіжність рядів.

1. - узагальнений гармонічний ряд.

2. .

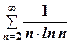Розв’язання. 1. Для знаходження функції замінимо у формулі загального члена дискретну змінну n неперервною змінною x, отримаємо

.

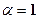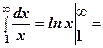
Нехай , отримаємо гармонічний ряд, , - інтеграл розбіжний, отже, і ряд - розбіжний.

Нехай 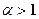. Тоді , - інтеграл збіжний, а отже, узагальнений гармонічний ряд 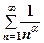- теж збіжний.

Нехай . Тоді - інтеграл розбіжний. Узагальнений ряд при - розбіжний.

5. Методичні поради при досліджені додатних рядів

При досліджені додатних рядів у деяких студентів виникають труднощі у виборі необхідної із викладених ознак. Так для застосування ознаки порівняння необхідно мати в розпорядженні певну множину уже досліджених рядів, щоб було з чим порівнювати. Таку множину можна утворити і поповнювати користуючись ознаками Даламбера, Коші (радикальною), інтегральною. При цьому рекомендується керуватись таким:

1. Якщо формула загального члена ряду містить факторіал або 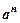, то зручно застосувати ознаку Даламбера.
2. Якщо легко добувати корінь n-го степеня із ,то застосовується радикальна ознака Коші.
3. Якщо не дуже складно обчислюється невласний інтеграл від функції , яку отримуємо заміною дискретної змінної n у формулі для неперервною змінною x, то застосовується інтегральна ознака. Часто інтегральна ознака застосовується комбіновано з граничною ознакою порівняння.

Ці поради носять орієнтовний характер, тому що не всі ряди можна дослідити за допомогою вказаних ознак. Відомі більш витончені ознаки збіжності рядів.

Приклади для самостійного розв’язання

Дослідити на збіжність ряди

1. .	2. .
3. .	4. .
5. .	6. .
7. 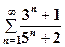.	8. .
9. .	10. .
11. .	12. .
13. .	14. .
15. .	16. .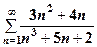
17. 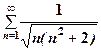.	18. .
19. .	20. .
21. .	22. .
23. .	24. .
25. .	26. .

Date: 2015-12-10; view: 732; Нарушение авторских прав