Властивості збіжних рядів

Теорема 1. Якщо ряд збігається, то збіжним буде і ряд, отриманий з даного шляхом відкидання (або приписування) скінченного числа членів.

Дійсно, нехай ряд

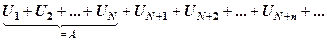(1)

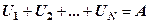є збіжним. Нехай в ньому сума перших доданків . Відкинувши в (1) перших доданків, отримаємо ряд

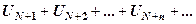(2)

Якщо часткова сума ряду (1)

,

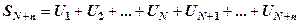а часткова сума ряду (2)

,

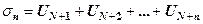то ці суми пов’язані між собою .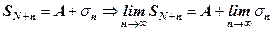

Останнє означає, що із збіжності ряду (1) випливає збіжність ряду (2), і навпаки.

Теорема 2. Якщо ряд збігається, то збіжним буде ряд .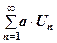

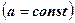Теорема 3. Якщо ряди і 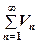збіжні і їх суми відповідно дорівнюють 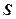і 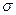, тоді збіжними будуть ряди

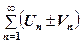(3)

суми яких відповідно дорівнюють 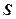+ 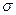і - .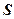

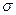Доведення теореми 2 і 3 базується на властивостях границь послідовностей частинних сум.

Наприклад, для доведення теореми 3 ми виходимо з припущення, що існують границі

,

,

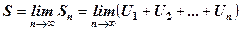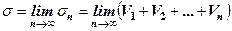а з цього випливає, що існує границя часткових сум ряду (3), тобто

.

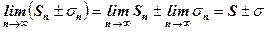Отже, ряд (3) теж збіжний.

Підкреслимо, що розглянуті властивості стосуються тільки збіжних рядів. Якщо ж хоча б один з рядів розбіжний, то теорема 3, наприклад, може не справджуватись. Для цього розглянемо ряд

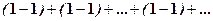(4)

який очевидно збігається, сума його дорівнює 0.

Ряд

1-(1-1)-(1-1)-…-(1-1)-… (5)

має своєю сумою 1.

А ряд

1-1+1-1+…+(-1)ⁿ⁺¹+…, (6)

який ми вже досліджували, є розбіжним.

Як бачимо, ряди (4),(5) і (6) різні. Властивості, що стосуються сум із скінченою кількістю доданків, не можна механічно переносити на ряди. Ряди мають свої особливості.

Date: 2015-12-10; view: 462; Нарушение авторских прав