Означення збіжності ряду. Сума ряду. Необхідна умова збіжності ряду

Розглянутий в прикладах 1-5 підхід до визначення суми ряду, якщо вона існує, узагальнимо на довільний ряд. Нехай дано ряд

(1)

Запишемо часткові суми цього ряду

, , ,…, .

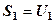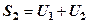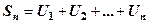Означення. Ряд (1) називається збіжним, якщо існує скінченна границя послідовності його часткових сум, тобто

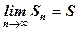. (2)

Число 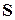називається сумою ряду, тоді можна писати

.

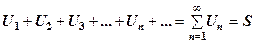Якщо ж границя часткових сум не існує, або дорівнює нескінченності, то ряд називається розбіжним.

З приводу розглянутих в попередньому параграфі прикладів можна сказати, що ряд (3) (приклад 1) є збіжним. Збіжним є ряд (5) (приклад 2).

Ряд (6) розбіжний,бо границя його часткових сум дорівнює нескінченності. Для ряду (10) границя часткових сум не існує, тому він теж розбіжний. Для ряду (8) (див. приклад 4) ми обчислили суму з високою точністю, хоча в його збіжності ми ще не переконались, це буде зроблено далі за допомогою ознаки Даламбера.

Звернемо увагу ще на такий факт: у всіх збіжних рядів, які ми вище розглянули, загальний член , якщо . З цього приводу має місце теорема.

Теорема (про необхідну умову збіжності ряду). Якщо ряд збіжний, то границя його загального члена при дорівнює нулю,

. (3)

Доведення. Поскільки , то 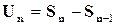. Із збіжності ряду випливає, що 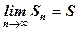і , тому

.

Наслідок. Якщо границя загального члена ряду (1) при не дорівнює нулю, тобто , то ряд розбіжний.

Доведення від супротивного. Припустимо, що ряд (1) збіжний, тоді згідно доведеній теоремі границя загального члена , але ж це протирічить умові наслідку, що . Тому наше припущення невірне.

Приклад. Дослідити на збіжність ряд .

Тут . Оскільки ,

то даний ряд є розбіжним.

Доведена теорема виражає тільки необхідну, але недостатню умову збіжності ряду, тобто із умови, що , ще не випливає збіжність. Ряд може бути як збіжним, так і розбіжним. Приклад цього є гармонічний ряд:

,

загальний член якого прямує до нуля, при , але цей ряд розбіжний. Дійсно розглянемо суму парної кількості доданків

Замінимо кожний з доданків найменшим 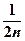, тобто , ,…, тоді

.

Отже, . Якщо припустити, що гармонічний ряд збіжний, тобто , то, переходячи до границі в нерівності при ,

отримаємо протиріччя: .

Значить, припущення невірне, і, отже, гармонічний ряд розбіжний, його часткові суми при .

Із викладеного тут видно, що більша увага надається поняттю збіжності ряду ніж, наприклад, наближеному обчисленню суми ряду, як це було зроблено при знаходженні числа 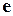. Справа в тому, що обчислювати суму ряду можна тільки тоді, коли є упевненість, що ця сума існує, тобто, що ряд збіжний. Так, наприклад, якщо б обчислювати часткові суми гармонічного ряду

за допомогою ЕОМ, не знаючи про його розбіжність, то можна було б отримати такі значення часткових сум 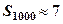, , . Часткові суми зростають досить повільно і можна було б якесь із їх значень прийняти за наближене значення суми ряду, а це було б помилкою, бо насправді при . Між іншим, для часткових сум гармонічного ряду існує цікава формула

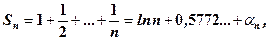де ,

яка дозволяє зрозуміти їх повільне зростання, бо , ,….

Отже питання збіжності ряду стає головним в подальших викладах.

Date: 2015-12-10; view: 482; Нарушение авторских прав