
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Практична робота № 5. Тема: Обчислення похідної за напрямом та градієнта функції багатьох змінних
|
|
Тема: Обчислення похідної за напрямом та градієнта функції багатьох змінних.
Мета: Навчитися на практиці застосовувати набуті знання.
Теоретичні відомості:
Якщо кожній точці  множини
множини 
 -вимірного простору
-вимірного простору  за деяким законом поставлено у відповідність одне і тільки одне дійсне число
за деяким законом поставлено у відповідність одне і тільки одне дійсне число  , то говорять, що в області
, то говорять, що в області  задано функцію
задано функцію  незалежних змінних
незалежних змінних
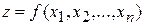 ,
,
де  – область визначення функції,
– область визначення функції,  – область значень функції.
– область значень функції.
Зокрема, коли  , маємо функцію двох змінних
, маємо функцію двох змінних  , якщо кожній парі
, якщо кожній парі  на площині поставлено у відповідність одне і тільки одне число
на площині поставлено у відповідність одне і тільки одне число  .
.
Позначимо частинні прирости функції  :
:
 ,
, 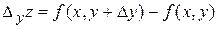 .
.
Якщо існують скінченні границі

то їх називають частинними похідними функції  у точці
у точці 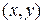 відповідно за змінними
відповідно за змінними  та
та  .
.
Позначення:  або
або  .
.
Правило знаходження частинних похідних першого порядку:
Для обчислення частинних похідних 
 користуються відомими формулами і правилами диференціювання функції однієї змінної, вважаючи всі змінні, крім змінної, за якою диференціюємо, сталими.
користуються відомими формулами і правилами диференціювання функції однієї змінної, вважаючи всі змінні, крім змінної, за якою диференціюємо, сталими.
Приклад 1. Знайти частинні похідні функції

Розв’язання.
З обмежень логарифмічної функції знаходимо область визначення функції. Функція визначена в області  . Вважаючи, що
. Вважаючи, що  стале, знаходимо
стале, знаходимо

Вважаючи, що  стале, знаходимо
стале, знаходимо

Функція  називається диференційованою в точці
називається диференційованою в точці  , якщо її повний приріст
, якщо її повний приріст  можна подати у вигляді
можна подати у вигляді

де 
 ;
;  – нескінченно малі при
– нескінченно малі при 
Повним диференціалом першого порядку  функції
функції  в точці
в точці  називається головна лінійна відносно
називається головна лінійна відносно 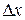 та
та  частина повного приросту функції:
частина повного приросту функції:

Так як  та
та  – незалежні змінні, то
– незалежні змінні, то 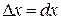 ,
,  .
.
Теорема. Якщо функція  диференційована в точці
диференційована в точці  і
і  , то в точці
, то в точці  існують частинні похідні, причому
існують частинні похідні, причому

Отже повний диференціал функції  обчислюється за формулою
обчислюється за формулою

Приклад 2 Задана функція  і точки
і точки 
 .
.
1) Обчислити значення 
2) Обчислити наближене значення  за допомогою повного диференціала;
за допомогою повного диференціала;
3) Знайти відносну похибку (у відсотках) при заміні приросту  диференціалом;
диференціалом;
4) Написати рівняння дотичної площини до поверхні  в точці
в точці 
Розв’язання.
1) Обчислимо значення 

2) Обчислимо наближене значення  за допомогою повного диференціала. Нехай
за допомогою повного диференціала. Нехай 








Підставимо знайдені значення у формулу (1):

3) Знайдемо відносну похибку при заміні приросту  диференціалом
диференціалом  .
.
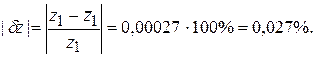
4) Знайдемо рівняння дотичної площини до поверхні  в точці
в точці  За попередніми обчисленнями
За попередніми обчисленнями 
 Тоді рівняння дотичної площини має вигляд
Тоді рівняння дотичної площини має вигляд
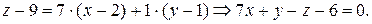

Нехай функція  визначена в деякому околі точки
визначена в деякому околі точки  ,
,  – вектор з початком у точці
– вектор з початком у точці  ,
,  – точка околу, що лежить на векторі
– точка околу, що лежить на векторі  ;
;  – довжина відрізка
– довжина відрізка  Якщо існує
Якщо існує

то ця границя називається похідною функції  за напрямом вектора
за напрямом вектора  у точці
у точці  , тобто
, тобто

Похідна за напрямом  характеризує швидкість зміни функції
характеризує швидкість зміни функції  у точці
у точці  за напрямом
за напрямом  .
.
Якщо функція  має в точці
має в точці  неперервні частинні похідні, то в цій точці існує похідна
неперервні частинні похідні, то в цій точці існує похідна  за будь-яким напрямом
за будь-яким напрямом  , причому
, причому
 (2)
(2)
де 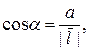


Вектор, координатами якого є значення частинних похідних функції  в точці
в точці  , називають градієнтом функції в цій точці і позначають
, називають градієнтом функції в цій точці і позначають 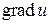 :
:

Вектор градієнта вказує напрямок найшвидшого зростання функції.
Завдання:
Таблиця вибору варіантів:
| а | в | с | а | в | с | ||
| -2 | |||||||
| -5 | |||||||
| -5 | -1 | ||||||
| -3 | |||||||
| -1 | |||||||
Завдання до виконання:
1.Обчислити похідну за напрямом вектора М1М2 та градієнт в точці М1, якщо М1(а;в), а М2(в;-с)
1. 
2 
3. 
2.Обчислити похідну за напрямом градієнта в точці М(с;-а)

Контрольні запитання:
1. Як знайти частинні похідні першого порядку?
2. Що таке похідна за напрямом?
3. Формула для знаходження градієнта.
4. Що характеризують градієнт та похідну за напрямом?
Date: 2015-10-19; view: 597; Нарушение авторских прав