
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Практична робота № 1. Тема: Побудова комплексних чисел на комплексній площині
|
|
Тема: Побудова комплексних чисел на комплексній площині. Дослідження застосування математичних операцій над комплексними числами.
Мета: Навчитись:
· виконувати математичні операції з комплексними числами;
· подавати комплексне число в різних формах;
· зображувати комплексні числа на комплексній площині;
· обчислювати модуль та аргумент комплексного числа.
Теоретичні відомості:
Алгебраїчна форма комплексного числа
Z=a+bi
Модуль комплексного числа
r=√a2+b2
Аргумент комплексного числа
| a | b | φ | |
| + | + | arctq |b|/|a| | |
| - | + | π - arctq |b|/|a| | |
| - | - | π + arctq |b|/|a| | |
| + | - | 2π- arctq |b|/|a| |
Тригонометрична форма комплексного числа
Z=r(cosφ+isinφ)
Показникова форма комплексного числа
Z=rei φ
Дії з комплексними числами в тригонометричній формі
Z1Z2=r1r2(cos(φ 1 +φ2)+isin(φ 1 +φ2))
Z1/Z2=r1/r2(cos (φ 1 -φ2)+isin (φ 1 -φ2))
Zn= rn (cos nφ+ i sin nφ)
√zn =√rn (cos (φ+2 πk/n)+i sin(φ+2 πk/n))
Дії з комплексними числами в показниковій формі
Z1Z2=r1r2ei( φ 1 +φ2)
Z1/Z2=r1/r2 ei( φ 1-φ2)
Zn= rneinφ
√zn =√rnei (φ+2 πk/n)
Завдання:
І. Знайти суму, різницю, добуток і частку комплексних чисел:
1. z1= 5 z2= -2i+1
2. z1= 2і+5 z2=  +і
+і
3. z1= -2і z2= 1+2і
4. z1= 2+і z2= 2-i
5. z1= 7-12і z2= 1+і 
6. z1= 1+і z2= 
7. z1= 5+4і z2=  -
-  і
і
8. z1= -1+і z2=  +і
+і
9. z1=  +і z2=
+і z2=  і
і
10. z1= -12+8і z2= 5+4і
11. z1= -16і z2= 2+5i
12. z1= -2і+1 z2= -2i
13. z1= 4-5і z2= 1+і 
14. z1= 2+ 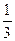 і z2= 5+4і
і z2= 5+4і
15. z1= -1+2і z2= 5+6і
16. z1= 2-2i  z2= 2+5i
z2= 2+5i
17. z1= 2+і z2= 5-і
18. z1= і z2= 2-  і
і
19. z1=  z2= і+5
z2= і+5
20. z1= 1+і z2= -  -і
-і
21. z1= -2  +і z2= 8
+і z2= 8
22. z1= 5-7і z2= 1
23. z1= 4+і z2= 5+2і
24. z1= 1-  і z2= 5
і z2= 5
25. z1= 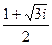 z2=
z2= 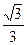 і
і
26. z1= 5 z2= 18-i
27. z1= 2+5і z2= 5-i
28. z1= 1+і  z2= -
z2= -  +
+ 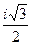
29. z1= 5-6і z2= 2i
30. z1= 7+і z2= 4-і
II. Подати комплексне число в показниковій та тригонометричній формах:
1. –1 11. –2-2і 21. -5
2. і 12. –2+і 22. 4і
3. -  13. 5-і 23. 1-2і
13. 5-і 23. 1-2і
4. –5і 14. 2+5і 24. –1+2і
5. 2-5і 15. 2-5і 25. 2-2і
6. –4-2і 16. 1-2і 26. –1+і
7. 5+і 17. –1-2і 27. і 
8. –6+2і 18. 5+0і 28.  -і
-і
9. 2+2і 19. 2+0і 29. -  і
і
10. –2+2і 20. 2-і 3 0. –5-5і 
ІІІ. Обчислити корені і результат зобразити на комплексній площині:
1. 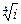 11.
11. 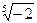 21.
21. 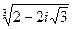
2.  12.
12. 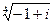 22.
22. 
3. 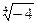 13.
13.  23.
23. 
4. 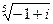 14.
14. 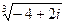 24.
24. 
5. 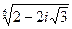 15.
15. 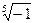 25.
25. 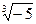
6.  16.
16. 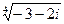 26.
26. 
7. 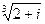 17.
17. 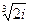 27.
27. 
8.  18.
18.  28.
28. 
9.  19.
19.  29.
29. 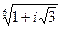
10. 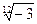 20.
20. 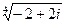 3 0.
3 0. 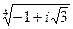
Контрольні запитання:
1. Чому виникає потреба в розширенні множини дійсних чисел?
2. Які форми запису комплексних чисел ви знаєте?
3. Операції з комплексними числами в алгебраїчній формі.
4. Операції з комплексними числами в тригонометричній формі.
5. Операції з комплексними числами в показниковій формі.
Date: 2015-10-19; view: 811; Нарушение авторских прав