Інтегрування раціональних дробів за допомогою розкладу на елементарні дроби

Перед інтегруванням раціонального дробу 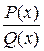необхідно зробити такі алгебраїчні перетворення та обчислення:

1) якщо задано неправильний дріб, то виділити з нього цілу частину, тобто подати його у вигляді

, де – многочлен, – правильний раціональний дріб;

2) розкласти знаменник дробу на множники

,

де 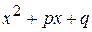має комплексні спряжені корені;

3) правильний раціональний дріб розкласти на суму елементарних дробів:

4) знайти невизначені коефіцієнти

,

для чого звести останню рівність до спільного знаменника, прирівняти коефіцієнти при однакових степенях в лівій і правій частинах отриманої тотожності і розв’язати систему лінійних рівнянь відносно шуканих коефіцієнтів. Можна визначити коефіцієнти іншим способом, надаючи в отриманій тотожності змінній довільні числові значення. Часто корисно комбінувати обидва способи обчислення коефіцієнтів.

Найпростіші дроби першого типу інтегруються по формулам

Найпростіші дроби другого типу в випадку п=1 інтегруються підстановкою

Формула, запам’ятовувати яку не потрібно.

Найпростіші дроби другого типу в випадку інтегруються тією ж підстановкою

Приклад 2. Знайти .

Розв’язання:

Розкладемо на множники знаменник:

.

Тоді

Прирівняємо чисельники дробів:

При будемо мати . При будемо мати . Запишемо попередню рівність у вигляді

Прирівняємо коефіцієнти при :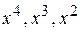

Отримали систему лінійних рівнянь, із якої знайдемо невідомі .

Тоді , а отже

Date: 2015-10-19; view: 548; Нарушение авторских прав